Agosto! As Feiras aproximam-se! Você deve participar. Essa é a finalidade de estudar e aprender: ser útil e transferir ao próximo sua parcela de Cultura. Aceite essas sugestões, as de seus prof4.6sores e seu esforço próprio para um bom desempenho na exposição de sua Escola.
Nota: Este artigo saiu numa Eletrônica Total 59 de 1993. Veja o perfil desse nosso colaborador e grande amigo.
Projeto 1 - Turbina a reação
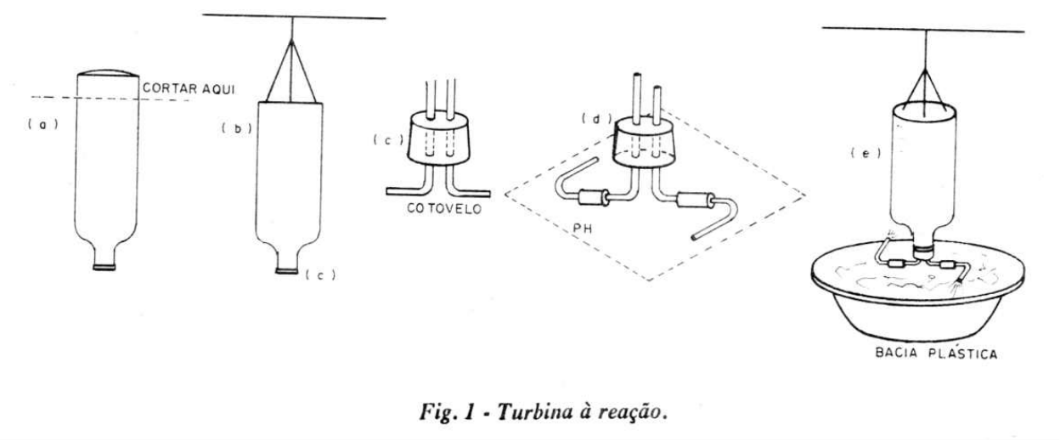
Na figura 1 temos a sequência de montagem desta experiência.
a) Corte o fundo de uma garrafa plástica para refrigerante tipo "Big". São embalagens descartáveis, de capacidade 2 litros.
Dê preferência àquelas transparentes e cujos rótulos são de plástico; esses são mais fáceis de serem arrancados do que aqueles de papel, que levam uma cola difícil de ser retirada.
b) Faça três furinhos simétricos (120°) 2 cm abaixo do corte. Amarre 3 pedaços de linha de pesca (número 50 ou 60) passando por esses orifícios e una-os em um só pedaço. Esse último pedaço deve ser preso a um suporte, mantendo a garrafa de boca para baixo. Obtenha uma rolha de borracha com 2 furos, que encaixe firmemente na boca da garrafa.
c) Pelos orifícios da rolha passe tubinhos de vidro em forma de cotovelo (90°). Esses tubinhos (conexões em L) podem ser obtidos em lojas de material de Química ou confeccionados na própria escola. Seu professor poderá ajudá-lo.
d) Mediante tubinhos de látex ("tripa de mico", muito comum em laboratórios químicos), adapte a esses cotovelos de vidro dois outros cotovelos que tenham uma das extremidades afiladas. Esses cotovelos de extremidades afiladas devem ficar no mesmo plano horizontal (PH) e apontando para sentidos opostos tipo torniquete.
e) Adapte firmemente o conjunto (d) à boca da garrafa e encha essa com água.
Os jatos laterais de água produzem forças de reação que originam um torque, pondo o conjunto a girar em sentido oposto aos dos jatos de água.
Expõe-se nessa experimentação o famoso princípio da ação e reação.
O experimento destaca também as forças que os líquidos aplicam nas paredes laterais. Nota: Nos barracões da FUNBEC, no Campus da Cidade Universitária (USP), há boa quantidade de material avulso para montagens didáticas, como as aqui sugeridas.
Projeto 2 - O carneiro Hidráulico (Golpe de Arlete)
A bomba "carneiro", ou carneiro hidráulico, é um dispositivo automático elevador de água.
Seu princípio de funcionamento é simples. Um fluxo de água atravessa o corpo do mecanismo; quando a velocidade desse fluxo atinge um valor adequado, uma válvula o interrompe abruptamente.
A energia cinética da água toda (não só a do corpo da bomba como também a da canalização) determina no corpo da bomba um violento golpe. Esse golpe é suficiente para empurrar uma certa quantidade de água a uma boa altura, sendo recolhida numa caixa d'água.
A bomba carneiro transforma a energia cinética da água em energia potencial. Seu rendimento hidráulico é pequeno.
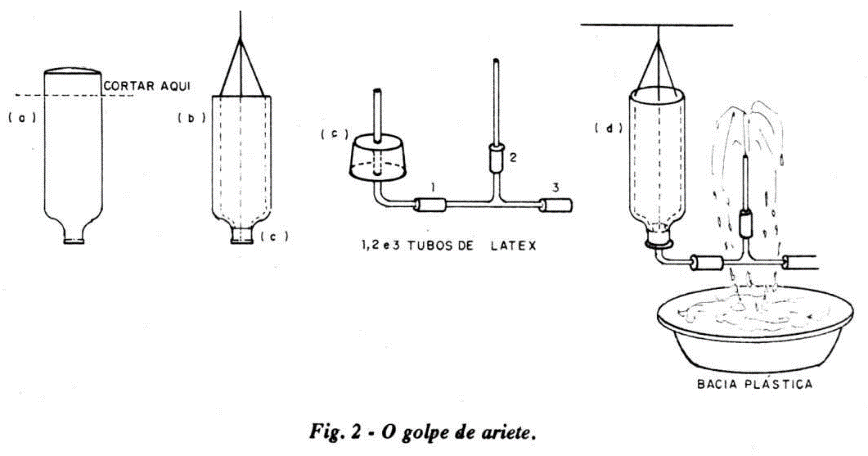
A montagem didática mostrada na figura 2 põe em destaque esse "golpe de aríete" devido à brusca interrupção do movimento da água e a sua consequente elevação.
Sequência de montagem:
a) Cortar a garrafa "big" de refrigerante na posição indicada. Veja item (a) do projeto 1.
b) Amarre 3 fios de linha de pesca no gargalo da garrafa. Passe suas extremidades livres pelos orifícios simétricos feitos na borda recém-cortada da garrafa e a seguir una-os em um só fio de pesca. Fixe o sistema a um suporte. Na boca da garrafa adapte uma rolha de borracha com 1 furo.
c) Pelo orifício da rolha passe um dos ramos de um cotovelo de vidro. Adapte um tubo de vidro em forma de T (junção 1) a esse cotovelo, mediante um tubinho de látex (1). Um tubo de vidro de extremidade afilada (tipo conta-gotas reto) é preso mediante látex (2) à perna central do T. Outro pedaço de tubo látex (3) é encaixado na extremidade livre do T.
d) Adapte o conjunto (c) na boca da garrafa e, apertando com os dedos o tubinho látex livre, encha a garrafa com água. Quando cheia, solte o tubinho de látex permitindo o escoamento de água. Aperte rapidamente esse tubinho, para interromper bruscamente a saída da água e fazer surgir o golpe de aríete. Repare na elevação de água na perna central do T. Na bomba carneiro real, esse estrangulamento é feito automaticamente. Veja, você aproveitou-se da própria energia da água para fazer subir a água!
Projeto 3 - Água em repouso e em movimento (Hidrodinâmica)
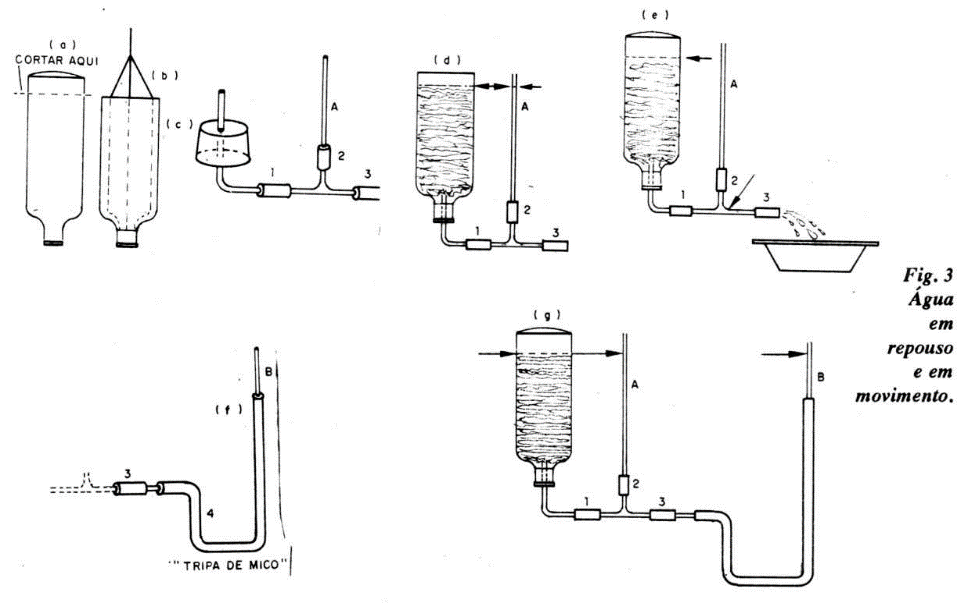
A sequência de experimentos a seguir tem por finalidade mostrar comportamento de líquidos quando em repouso e quando em movimento. A situação de movimento é campo da hidrodinâmica; nesse aspecto, as experiências f, g, h e i da figura 3 são justificações da lei de Bernoulli:
Ao longo de uma linha de fluxo a expressão: permanece com valor constante. pressão dinâmica e “svz” é a pressão
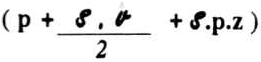
Na expressão, p é a pressão estática, “s.v” é a hidrostática ou de posição. /2
a) Veja item (a) do projeto 2
b) Veja item (b) do projeto 2
c) Veja item (c) do projeto 2.
Aqui a diferença é o tamanho do tubo de vidro (A) ligado à perna central do T. Agora ele chega acima do nível do fundo aberto da garrafa plástica.
d) Coloque o dedo vedando a saída do tubinho de látex (3). Preencha a garrafa com água. Observe que, com o líquido em repouso, o nível em (A) é igual ao nível da água na garrafa. Em equilíbrio, pontos de mesma pressão hidrostática pertencem ao mesmo plano horizontal.
e) Retire o dedo do tubinho (3) e permita o escoamento da água. Repare que, nessa fase, o nível da água em (A) cai praticamente a zero. Na junção do T a velocidade aumentou e, portanto, a pressão total diminuiu (isso é uma variante do tubo de Venturi).
f) No tubinho de látex (3) encaixe uma junção de vidro e nessa um tubo de borracha (4), plástico ou látex (tripa de mico), de 50 cm de comprimento. Adapte um tubo de vidro (B) de 10 cm na extremidade livre desse longo tubo. Tal tubo, em plástico transparente e flexível, é facilmente encontrado em lojas de aquários.
g) Com o dispositivo na posição ilustrada, preencha a garrafa com água. Repare novamente que, no repouso, os três níveis são iguais (A, B e garrafa). Chame a atenção do expectador que isso (igualdade dos níveis) é sempre verdade, independentemente dos volumes de água na garrafa, em (A) e em (B). Essa observação curiosa constitui o "paradoxo hidrostático".
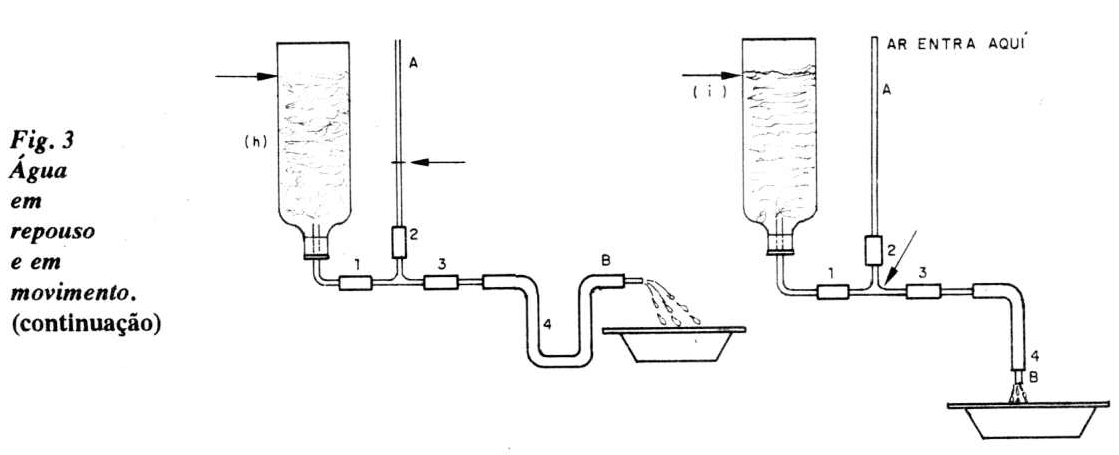
h) Coloque o tubo (B) na horizontal e mantenha o dedo em B, vedando a saída de água. Observe que os níveis na garrafa e em (A) permanecem iguais e o mesmo do item (g).
Retire o dedo e permita o escoamento da água. Durante o escoamento repare na nova posição do nível em (A). Veja que a situação é diferente do caso (e). Por quê?
i) Leve o tubo (4) para a posição vertical, permitindo uma maior diferença de pressão hidrostática. O nível em (A) não só cai a zero, como também ar é aspirado. A pressão aí caiu demais, tornou-se "negativa". Pressão negativa é uma "sucção".
Viu quanta coisa para mostrar, quanta coisa para estudar e perguntar?
Projeto 4 - A fonte de Heron
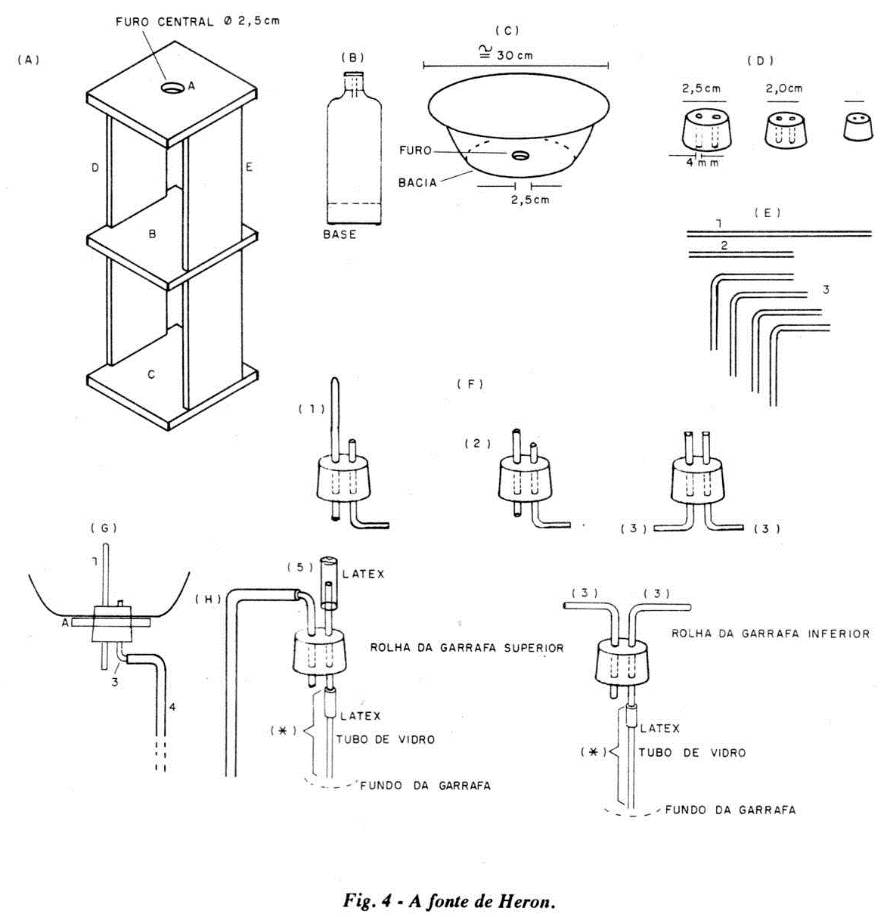
Com tal montagem você conseguirá facilmente um jato de água de 50 cm de altura, de modo contínuo, por mais de 20 minutos, usando apenas, como energia inicial, o trabalho de colocar a garrafa cheia de água na plataforma B. Eis o material necessário:
a) 3 placas de madeira (A, B, C) de 0,5 cm de espessura e lados de 15 cm; 2 sarrafos (D e E) de 1 cm de espessura, 5 cm de largura e 150 cm de comprimento. Veja em (a), na figura 4, a montagem dessas peças, formando a "prateleira" de 3 patamares A, 13 e C.
b) 2 garrafas de refrigerante tipo "Big", em plástico, com capacidade de 2 litros.
c) 1 bacia de plástico, redonda, com diâmetro de cerca de 30 cm, com um furo central em seu fundo, com diâmetro de 2,5 cm. Uma forma de pizza também serve.
d) 3 rolhas de borracha, com dois furos cada; uma que se adapte ao furo da bacia e pelo orifício da plataforma A e as outras duas que serviam para as bocas das garrafas plásticas. Todos os furos nas rolhas devem permitir a passagem de tubos de vidro de 6 ou 7 mm de diâmetro externo.
e) 1 tubo de vidro (6 mm) com uma das extremidades afunilada e cerca de 15 cm de comprimento (1); 1 tubo de vidro reto com cerca de 8 cm de comprimento (2); 4 tubos de conexão em L (cotovelos em 90°), com pernas de 5 cm de comprimento (3).
f) Na rolha grande passam os tubos (1) e (3); numa pequena passam os tubos (2) e (3) e na última passam os dois tubos restantes (3).
g) Coloque o fundo da bacia na plataforma A, com os furos coincidindo. Pela face inferior de A, introduza a rolha grande no furo, até parte da rolha sobressair do fundo da bacia. No ramo horizontal do cotovelo (3) adapte um tubo de plástico transparente ou "tripa de mico" (4). Você precisará, ao todo, de uns 3 metros desse tipo de tubo flexível.
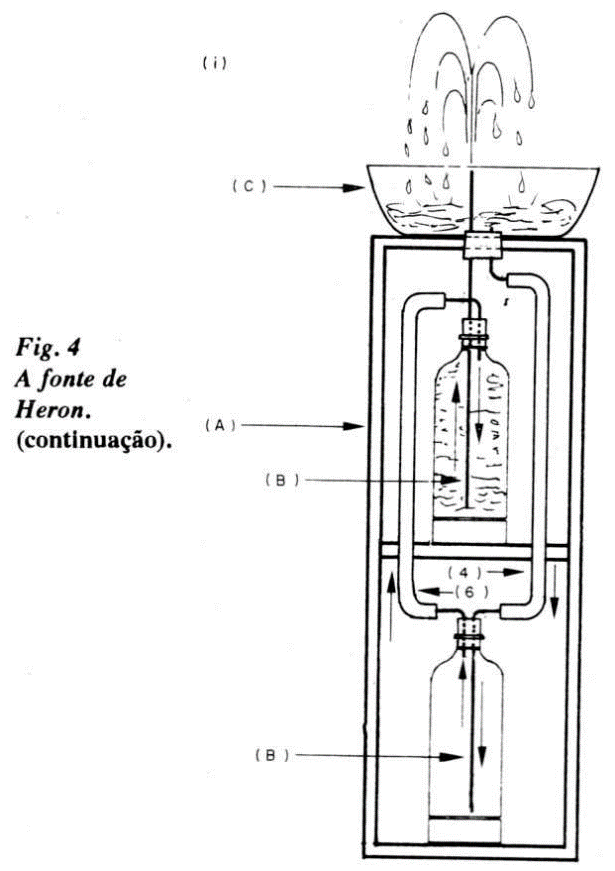
h) Na rolha que vedará a garrafa superior (já com seus tubinhos de vidro), coloque pequenos pedaços de tubo flexível (látex ou tripa) nas extremidades.
Na conexão plástica do tubo reto, adapte um tubo de vidro que chegue até o fundo da garrafa. Você pode substituir esse tubo de vidro por um tubo de plástico flexível que chegue até o fundo da garrafa. Faça o mesmo com um dos tubos de vidro da garrafa inferior. Na figura 4, (6) é um pedaço do tal tubo flexível em plástico ou tripa.
I) Montagem final: Coloque água até o gargalo na garrafa superior e adapte sua rolha bem firme (não pode vazar ar). Coloque essa garrafa na plataforma B e encaixe o tubinho de látex (5) na extremidade inferior do tubo de vidro afunilado da bacia.
Coloque a rolha na garrafa inferior (vazia) bem apertada!
Adapte a "mangueirinha" (6) que sai do cotovelo (3) da garrafa superior no cotovelo (3) (da esquerda) da garrafa inferior. Essa é a hora de você ajustar o comprimento correto da "mangueirinha", antes de cortá-la definitivamente.
Adapte a mangueirinha que vem da bacia ao cotovelo (3) (da direita) da garrafa inferior. Esse é o cotovelo que tem a tal emenda que vai até o fundo da garrafa. Para funcionar, basta colocar um pouco de água na bacia, até cobrir a boca do tubo (3) que sobressai ligeiramente da rolha.
Daí para a frente a "coisa" funciona "por conta própria".
Explicação: A água colocada na bacia penetra na mangueira e vai até a garrafa inferior, forçando a saída de ar dessa garrafa. O ar que sai entra na garrafa superior, via (6), aumentando a pressão nos pontos do interior dessa garrafa. Isso força a água a jorrar pelo tubo afunilado. A água que jorra cai na bacia, entra na mangueira e vai para a garrafa inferior, forçando mais saída de ar dessa.
E o processo continua até que toda a água da garrafa superior passa para a inferior. Depois, é só afrouxar as rolhas e trocar as garrafas de posição (cheia em cima, vazia em baixo). Vale a pena ver isso funcionar!
Projeto 5 - Fonte refrigerante
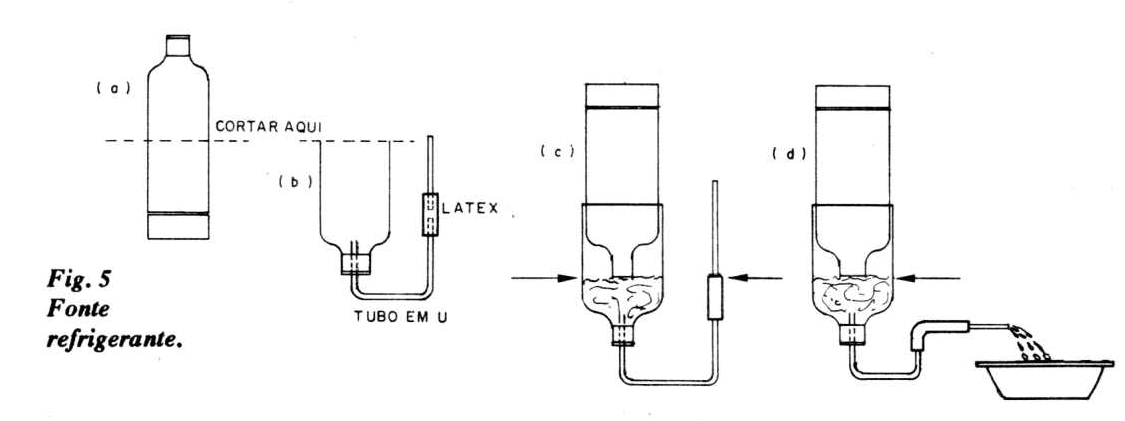
Sirva refrigerante aos visitantes da Feira, mediante uma fonte. Na figura 5 temos os detalhes e a montagem da fonte para refrigerantes.
a) Corte, um pouco acima da metade, uma garrafa plástica (refrigerante "Big", 2 litros, rótulo de plástico).
b) Adapte à sua boca uma rolha com um furo. Neste furo force um dos ramos de um tubo de vidro em U. Emende, mediante um tubinho de látex (ou tripa de mico), um tubo de vidro reto na extremidade externa do U.
c) Mantenha o tubo de vidro reto, na vertical. Encaixe na garrafa cortada uma garrafa cheia de refrigerante. O refrigerante sairá da garrafa cheia até que o nível na garrafa inferior chegue á boca da superior. Veja o nível no tubo externo: é igual!
d) Agora é só abaixar o tubo reto e servir o refrigerante. Após servida essa dose, retorne o tubo reto para a vertical.
Nota: Para que a garrafa cheia encaixe bem na garrafa cortada proceda assim: após o corte da garrafa, mergulhe essa extremidade recém-cortada em água quente e force uma outra garrafa igual nessa abertura, de modo a alargar um pouco a região recém-cortada.
Projeto 6 - Dupla fonte
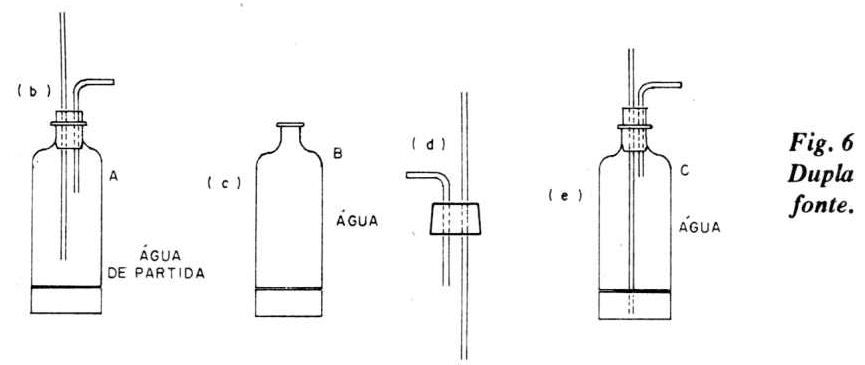
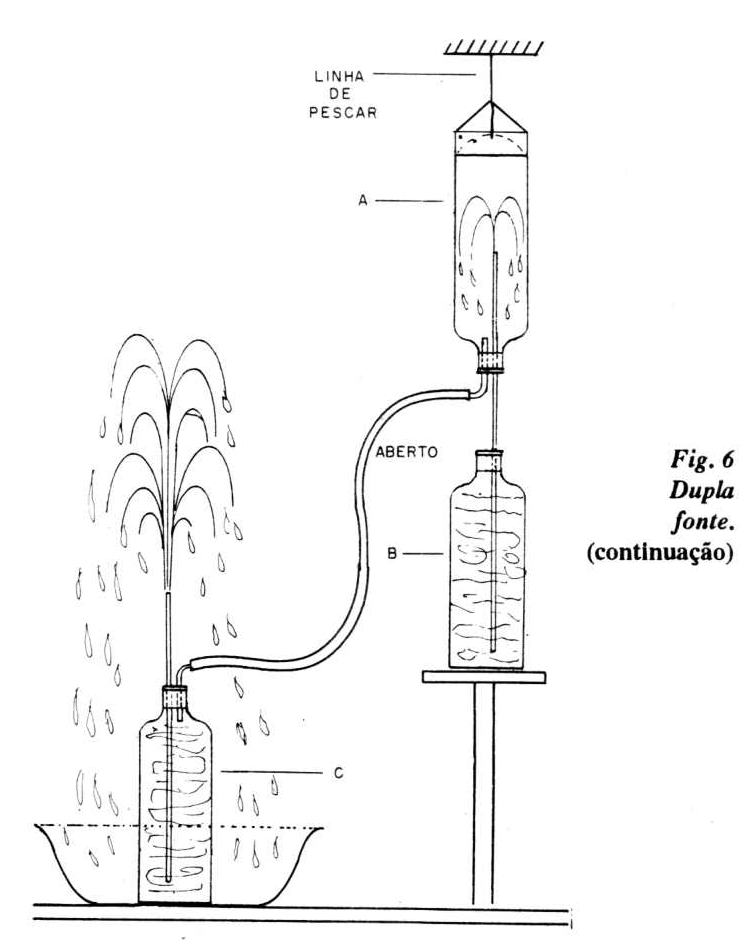
As ilustrações deixam bem clara essa montagem simples. Vamos usar 3 garrafas de refrigerante "Big", de 2 litros, duas rolhas com dois furos, dois cotovelos de vidro (6 mm), com dois longos tubos de vidro com uma das extremidades afuniladas, tubo de plástico flexível (ou "tripa de mico") e uma bacia.
Na figura 6 temos os detalhes de montagem da dupla fonte.
O processo se inicia pelo pouco de água contido na garrafa A.
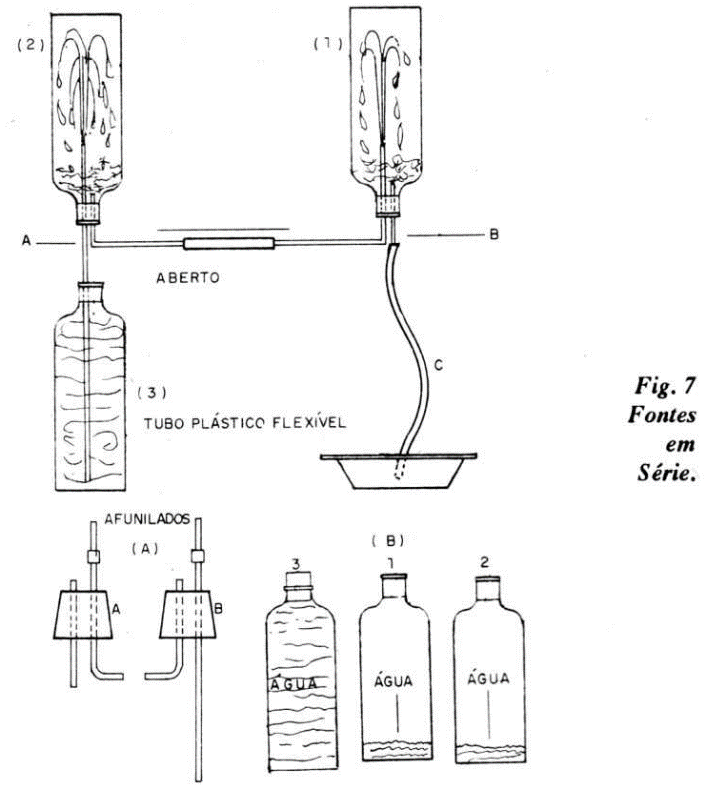
Projeto 7 - Fontes em série
Nesse projeto utilizaremos: 3 garrafas de refrigerante (Big - 2 litros), 2 rolhas com dois furos, 2 cotovelos de vidro com uma das extremidades afuniladas, 3 tubos de vidro retos, 4 uniões de látex (ou tripa de mico), 1 tubo de plástico flexível de 1,5 m (ou tripa), balde ou bacia e água.
Na figura 7 temos os detalhes de montagem das Fontes em série.
Observe que a garrafa (3) se inicia cheia e as (1) e (2) com apenas 2 ou 3 cm de água; o suficiente para cobrir as extremidades dos tubinhos de vidro retos que penetram pelas rolhas. A colocação das garrafas (1) e (2) na vertical determina o início do processo.
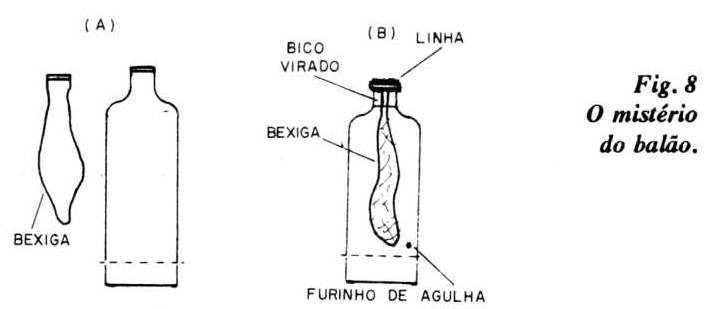
Projeto 8 - O mistério do balão
Que tal olhar para o interior de um balão de borracha (bexiga) cheio de ar (inflado) e com o bico aberto?
Para encher um balão de aniversário com ar, você assopra pelo bico, vencendo não só a pressão atmosférica como a pressão elástica do próprio balão. A seguir, amarra o bico e lá está o balão pronto para a festa. Vamos agora encher o balão por técnica oposta, ou seja, vamos manter o bico aberto e diminuir a pressão na face externa do balão. Isso é fácil, veja a montagem ilustrada na figura 8.
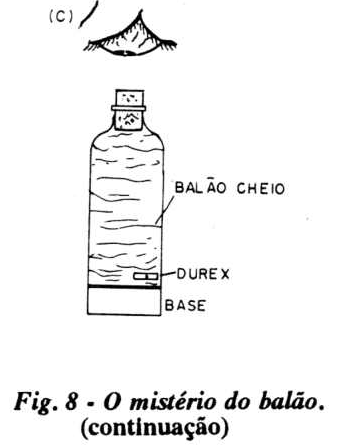
a) Enfie um balão de borracha vazio, pelo gargalo da garrafa de refrigerante (Big - 2 litros). Vire o bico sobre o gargalo, de modo a envolvê-lo, e amarre as bordas com os punhos de elástico ou cordonê, mantendo-o aberto para a atmosfera. b) Próximo à base de apoio da garrafa, faça um pequeno orifício com uma agulha ou ponta de compasso.
c) Coloque sua boca contra esse furinho e aspire o ar do interior da garrafa. Tape com a língua ou com o dedo, entre etapas sucessivas de aspiração. Com isso, o balão irá se enchendo. Continue aspirando até que o balão preencha quase todo o volume interno da garrafa. Quando achar que o balão está bem cheio, tape o furinho com 3 cm de fitas durex transparente.
Lá está o balão cheio e com o bico aberto! Dê uma boa olhada lá dentro (e deixe os espectadores olharem também!). Sem dúvida irão lhe perguntar como você conseguiu tal proeza. Explique tudo direitinho, sem mistérios ou coisas do além; isso é Ciência e não tapeações baratas!
Projeto 9 - O soluço da garrafa
Faça a montagem a seguir ilustrada na figura 9, onde utilizaremos uma garrafa "big" cortada, uma garrafa "big" normal, duas rolhas com um furo cada, um tubinho de vidro e água quente.
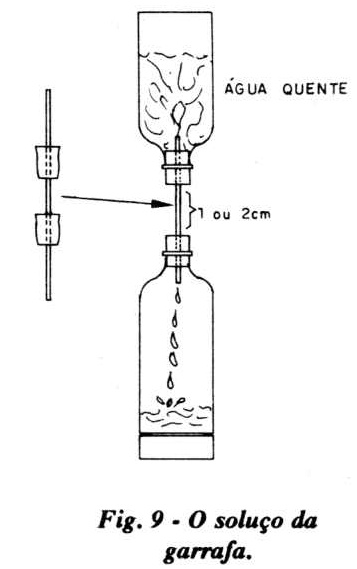
Adapte as rolhas em ambas as garrafas e passe o tubinho através dos furos, unindo-as. Vire o conjunto, com a garrafa sem fundo para cima, e despeje a água. É só! Repare no que acontece (e explique!).
Você sempre deve consultar seu professor e livros. Se encontrar sempre tudo "mastigadinho", e pronto para apresentação, sua participação seria apenas a de um mero intermediário -o Brasil já está superlotado desses "parasitas científicos!"
Projeto 10 - Garrafas ressonantes
Esse projeto, apesar de utilizar garrafas e apresentar o título "ressonantes", nada tem de hidrostática nem de acústica, é um projeto de mecânica das oscilações acopladas.
A explicação do funcionamento, para alunos do primeiro grau, pode ser apoiada no fenômeno da ressonância, coisa que ocorre quando dois sistemas apresentam a mesma frequência natural de oscilação e estão acoplados por um meio elástico.
O que vamos fazer é montar dois pêndulos (de garrafa) e prender seus fios de suspensão a um outro fio que funcionará como acoplamento. As garrafas devem ser totalmente preenchidas com água e suspensas por fios de linha de pesca que passem pelos centros das tampas. Use garrafas do mesmo formato, porém de cores diferentes, para maior destaque e rapidez de identificação.
Se ambas forem transparentes, preencha-as com água colorida, digamos, vermelha e verde.
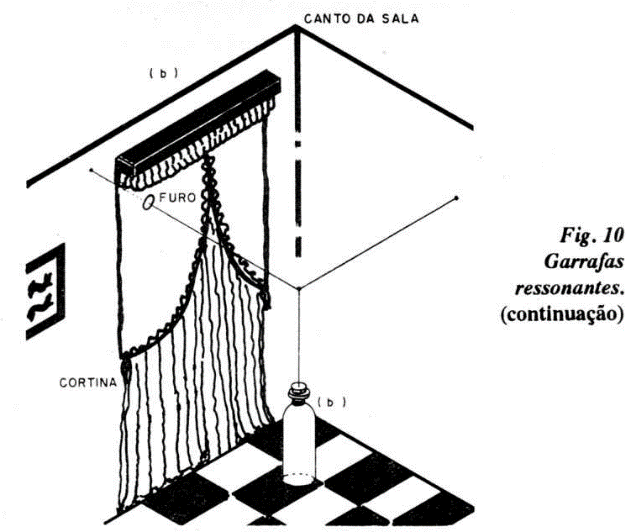
Em duas paredes próximas (ou num canto da Feira), faça furos à dois metros de altura, coloque buchas plásticas e parafusos com cabeça de argola. Se os apoios forem de madeira, use pitões de argola. Amarre um fio de linha de pesca (50 ou 60) entre essas argolas, deixando o fio "bambo", como mostra a figura 10.
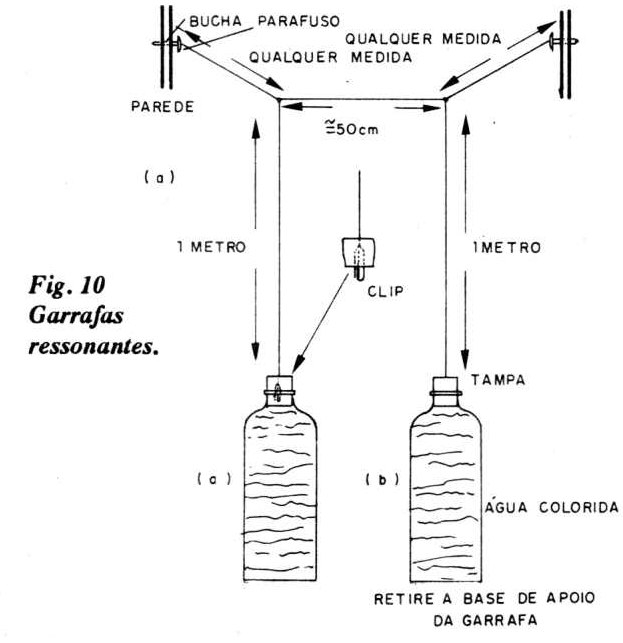
Amarre o fio de suspensão de uma das garrafas (que tem cerca de 1 m de comprimento) a esse fio colocado entre as argolas.
Posta a oscilar, essa garrafa o fará com determinado período (tempo para uma oscilação completa). A outra garrafa, quando suspensa (afastada cerca de 50 cm da primeira), deverá oscilar exatamente com os mesmos períodos. Para isso deve-se proceder a um ajuste rigoroso no comprimento do fio de suspensão da segunda garrafa. Comece amarrando-o com cerca de 1,05 m e depois vá diminuindo até obter a igualdade dos períodos.
Como observar isso? É fácil: deixe uma das garrafas (pode ser a que está sendo ajustada) parada e afaste a outra de uns 20 cm, lateralmente, de sua posição de equilíbrio e solte.
A garrafa que oscila transmitirá energia mecânica através do fio até a outra garrafa, que começará lentamente a oscilar. Se os períodos estiverem criticamente ajustados, toda energia mecânica da primeira deverá ser transmitida para a segunda, parando totalmente de oscilar.
Esse é o modo correto do ajuste, a primeira deve parar completamente! A segunda, agora, deverá estar oscilando com amplitude máxima. A seguir inicia-se o retorno da energia da segunda para a primeira, até que a segunda para completamente.
Esse vai e vem da energia mecânica continua, com amplitudes cada vez menores (devido às resistências dissipativas), até tudo parar. Isso leva uns bons 20 minutos ou mais.
Se fossemos incentivar charlatanismos, com "forças mentais", "ondas mentais", "forças do pensamento" ou algo do gênero, sugeríamos colocar uma cortina escondendo uma das garrafas (bastaria um furinho na cortina para passar o fio de acoplamento) e diríamos que através de tais "forças" faríamos a garrafa (a única visível!) começar sozinha a se mover e depois parar!
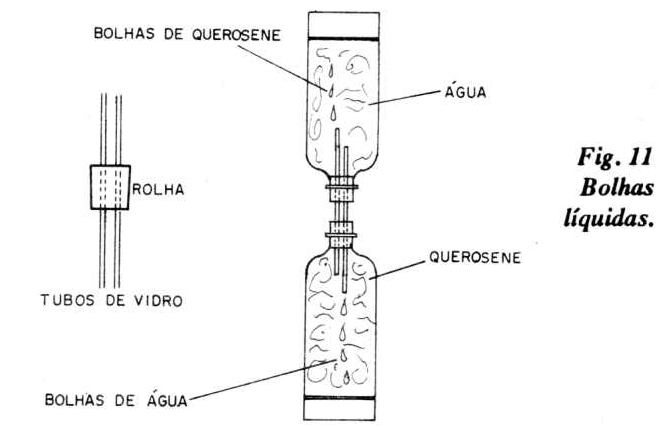
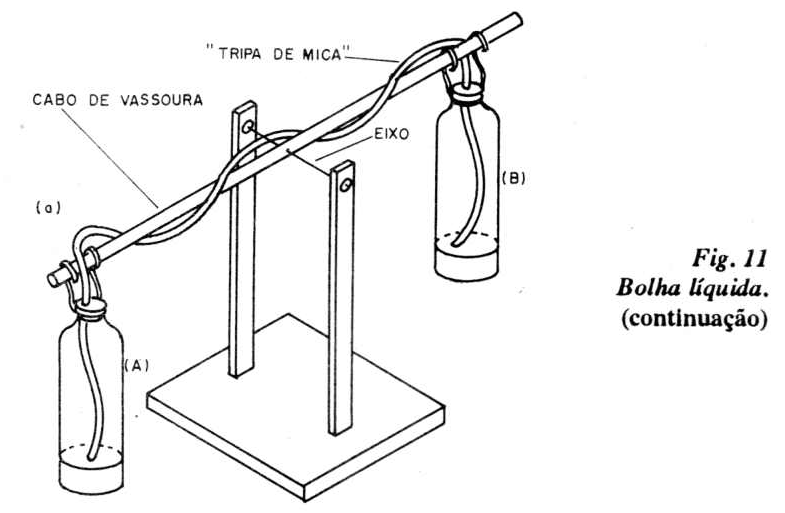
Projeto 11 - Bolhas líquidas
As diferentes massas específicas (ou densidades absolutas) dos líquidos utilizados nesse experimento são as causas das bolhas líquidas visualizadas. A garrafa plástica (Big 2 litros) inferior é preenchida com querosene, e a superior com água. A rolha (com os dois tubos de vidro) permite a fixação entre elas. Um pouco de cola de silicone e fita adesiva completam o trabalho de fixação.
Após a passagem completa do querosene para a garrafa de cima, em bolhas, e da água para a de baixo, também em bolhas, inverta o sistema para começar tudo de novo.
Na figura 11 ilustramos este experimento.
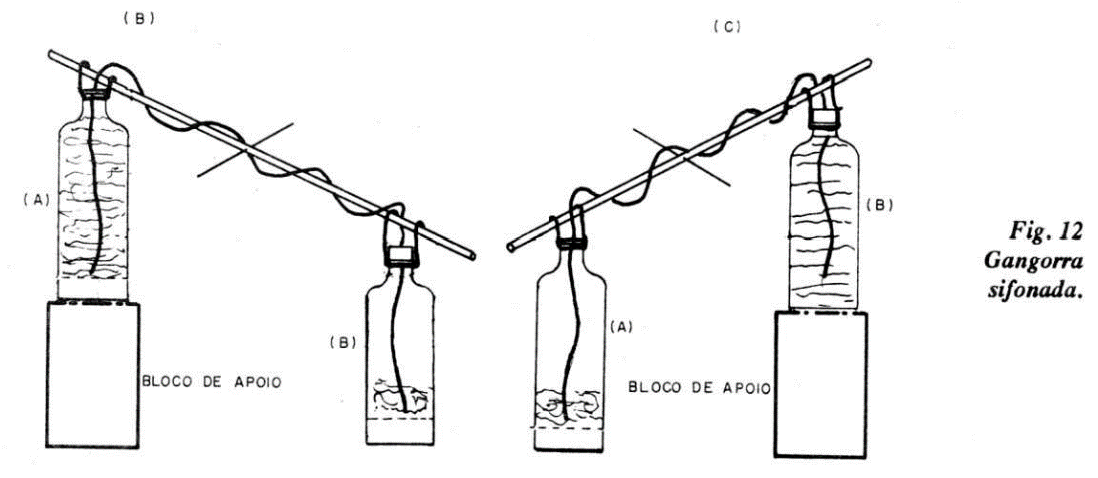
Projeto 12 – Uma gangorra sifonada
Na figura 12 temos a ilustração deste projeto.
Coloque A em cima e B em baixo (b). Aspire pelo tubo (retire a extremidade que está dentro de B) até que a água inicie o escoamento, por sifonagem, e mergulhe o tubo em 13, até o fundo. Nessa situação teremos a passagem de A (em cima) para B (em baixo). Quando A estiver quase vazio, inverta a gangorra (A em baixo, B em cima) (c).
Como o sifão está cheio de água, a sifonagem continua, porém de B para A. Quando B estiver quase vazio, inverta a gangorra novamente, e assim sucessivamente.
Nota importante: Algum espertinho poderá imaginar um sistema de polias (ou algo semelhante) para inverter automaticamente a gangorra: não vai funcionar - moto contínuo é utopia!
Projeto 13 - Escoamento de líquidos I
Material: Balde com torneira (ou parte inferior de um filtro caseiro para 3 ou 5 litros), copos comuns para água e relógio.
Na figura 13 temos a ilustração da montagem.
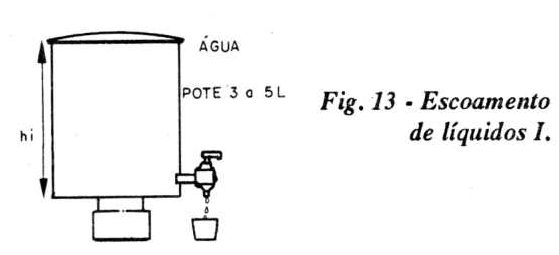
Procedimento: Coloque um copo sob a torneira, abra a torneira e determine, mediante o relógio, o tempo necessário para encher esse copo com água. Suponha que o intervalo de tempo para o total do enchimento do copo seja de 30 segundos.
Pergunta: Se o recipiente contém 30 copos de água e você deixar a torneira aberta, em quanto tempo ficará totalmente vazio?
Parece simples? Vejamos, se um copo d'água escoa em 30 segundos, 30 copos de água escoarão em 30x30 segundos, ou seja, 15 minutos!
A melhor maneira para comprovar que isso está errado é fazer uma experiência. Proceda assim:
Com o material à mão, preencha uma tabela, indicando quanto tempo necessita-se para encher copo a copo. Para preencher o primeiro copo foram necessários 30 s (no exemplo -faça sua experimentação real); para encher o segundo copo são necessários...segundos, e assim sucessivamente. Vá anotando na tabela.
Somando-se todos esses intervalos de tempo, até o trigésimo copo, você obterá coisa de meia hora, e não 15 minutos!
Você deve ter observado, pela tabela, que o tempo de escoamento (para um dado volume, o do copo), e, portanto, a vazão da água, não permanece constante.
Após o preenchimento do primeiro copo, o nível da água no reservatório baixou. Isso determina uma menor pressão no fundo do recipiente, o que acarreta menor velocidade de escoamento da água e, consequentemente, maior tempo para escoar um dado volume.
A velocidade com que um líquido jorra por um orifício aberto na parede lateral do recipiente aberto depende da altura do líquido, contada desde o orifício até a superfície livre. A expressão de Torricelli para tal velocidade de escoamento é:
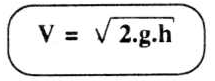
onde V é a velocidade com que o líquido jorra, g a medida da aceleração da gravidade no local e h é o desnível entre o orifício e a superfície livre. Conclui-se, desse experimento:
1 - a vazão do líquido não é constante;
2 - se depois de vinte copos cheios o nível da água (h) caiu a um quarto do nível inicial (h) com reservatório cheio, o vigésimo copo levará o dobro do tempo para ser preenchido, relativamente ao primeiro copo;
3 - se o nível da água cair a um nono do inicial do, o tempo de enchimento do copo nessa fase será o triplo do tempo de enchimento do primeiro copo;
4 - um rigoroso cálculo matemático comprova que, para esvaziar um reservatório de capacidade V, necessita-se do dobro do tempo que aquele que seria necessário para es-coar o mesmo volume, mantendo-se o nível constante;
Nota: os problemas de vazão de líquidos com níveis não constantes não podem ser resolvidos com aritmética, e sim com cálculo integral.
5 - o escoamento de um líquido não depende da densidade absoluta do líquido. Desde que o desnível inicial seja o mesmo, água, álcool, mercúrio etc, escoarão ao mesmo tempo (mesmo volume, mesma abertura).
Veja próximo experimento, no projeto 14.
6 - o escoamento (vazão) não depende da forma do recipiente.
Projeto 14 - Escoamento de líquidos II
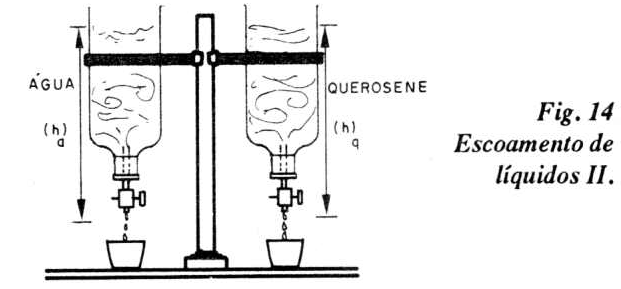
Material: Dois frascos com torneiras idênticas (não é necessário que tenham mesma forma) e líquidos diferentes (exemplo, água e mercúrio, água e querosene etc).
Na figura 14 ilustramos a montagem. Água e querosene, ao mesmo nível, com torneiras idênticas, escoam volumes iguais em tempos iguais! Veja experimento anterior.
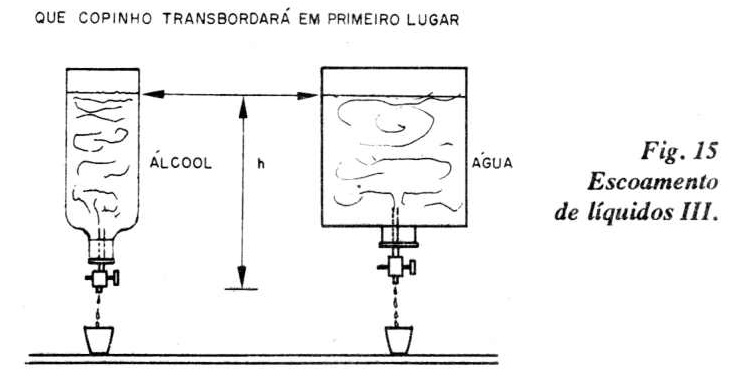
Projeto 15 - Escoamento de líquidos III
Na figura 15 mostramos o esquema desta montagem, cujo princípio de funcionamento é o mesmo do projeto anterior, evidenciando, apenas que a vazão é independente da forma do recipiente.
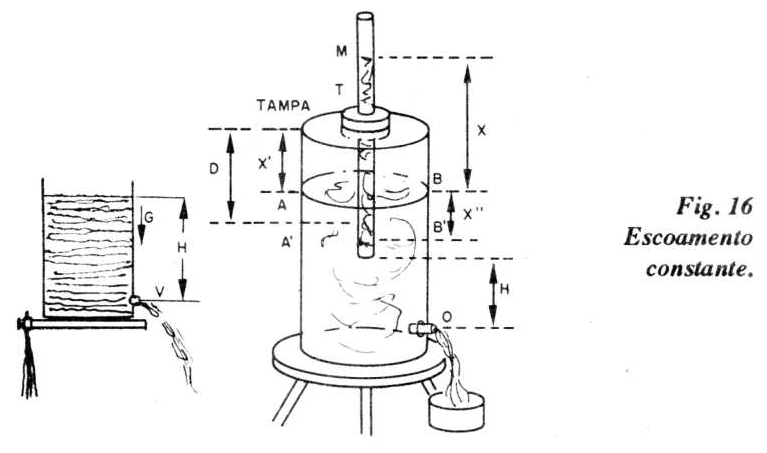
Projeto 16 - Escoamento constante
1. Lei de Torricelli: Conforme comprovamos nos três experimentos anteriores, a vazão (volume de líquido que escoa por unidade de tempo) não é constante, devido ao abaixamento do nível de líquido.
Como vimos, isso é quantificado pela lei de Torricelli que, com roupagem nova, escreve-se:
"Quando um líquido escoa por um orifício praticado numa parede de um frasco aberto, a velocidade de escoamento é igual àquela adquirida por um corpo em queda livre, no vácuo, caindo de uma altura igual à distância da superfície livre até o centro do orifício"
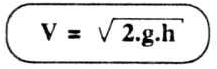
Na figura 16.1 ilustramos o que foi dito.
Para manter a vazão constante, lançamos mão do artifício a seguir.
2. Vaso de Mariotte: o dispositivo permite um escoamento à velocidade constante, apesar da diminuição da altura h.
A montagem é mostrada na figura 16.2
Consiste em um frasco com gargalo e munido de uma rolha atravessada por um tubo de vidro T. Suponha que no início o orifício. O do frasco esteja tapado. No interior do frasco o líquido encontra-se no nível AB, e no tubo T, no nível M, x acima da superfície livre.
Nessa situação inicial, o ar dentro do frasco encontra-se sob pressão H+x, onde H é a pressão do ar exterior (pressão atmosférica no local da experiência, medida em altura de coluna do líquido em questão).
A questão total ao nível do orifício será H+x+OB.
O volume de ar interno é x'.A, onde A é a área da secção transversal do frasco cilíndrico (despreza-se a área da secção do tubo, pois participará igualmente de todo o equacionamento, cancelando-se).
Abrindo-se o orifício, esta sobre pressão x+OB inicia o escoamento do líquido, com velocidade decrescente, pois o nível AB baixa, assim como o nível M no tubo. Essa fase inicial de escoamento não constante perdura por breve intervalo de tempo; exatamente aquele necessário para que o nível M coincida com a extremidade inferior do tubo (o tubo fica vazio).
A pressão do ar interno cai a um valor abaixo da pressão atmosférica H (devido ao abaixamento de AB).
Desse modo, uma bolha de ar entra no interior do frasco, via tubo, igualando a pressão ao nível da extremidade inferior do tubo. Não há diferença de pressão entre o nível inferior do tubo e o nível da superfície livre. Para o orifício é como se aquela camada líquida acima da extremidade inferior do tubo não existisse.
Essa é a altura efetiva (da extremidade inferior do tubo até o centro do orifício) que determina escoamento constante, com líquido saindo com velocidade V2gh Se você pretende incluir em seu folheto da Feira de Ciências uma demonstração algébrica da condição de escoamento constante, sugerimos a seguinte:
Seja A'B' o nível líquido dentro do frasco, num instante qualquer, e N o nível no tubo, nesse mesmo instante genérico.
A lei de Boyle, aplicada ao ar dentro do frasco nos instantes iniciais e nesse instante genérico, permite escrever:
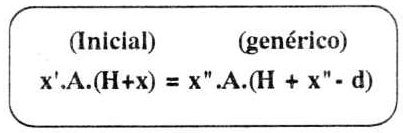
A partir dessa situação genérica, o nível baixa simultaneamente no frasco e no tubo, de modo que x"-d tende a anular-se. Nesse instante teremos:
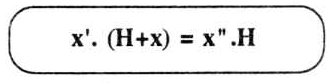
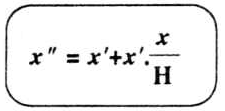
Enquanto essa situação for satisfeita, estará garantida que a pressão ao nível inferior do tubo é a pressão atmosférica e, consequentemente, a constância da velocidade de escoamento.
Notas:
a) Regulando-se h para um valor pequeno, obtém-se um gotejamento bastante regular.
Tal gotejamento era utilizado, antigamente, como relógio.
b) O borbulhamento pelo tubo também é bastante regular.
c) Se for praticado um pequeno orifício no frasco, ao nível inferior do tubo, por ele não escoará água pois, não há diferença de pressão.
d) Se for praticado um pequeno orifício no frasco, pouco acima do nível inferior do tubo, não escoará água por ele, pelo contrário, ar entrará por ele, pelo fato de que nesse nível a pressão é menor que a atmosférica.