9.1 – Os tipos de contadores
Em eletrônica digital devemos separar os circuitos lógicos sem sincronismo algum, daqueles que possuem algum tipo de sincronismo externo, ou seja, usam um sinal de CLOCK.
Existem, portanto, circuitos que se enquadram no que se denomina lógica simples e no que se enquadra no que se denomina lógica sincronizada.
O que ocorre é que existem aplicações em que, tudo que importa para o circuito, é fazer uma operação com determinados níveis lógicos aplicados à sua entrada quando eles estão presentes, não sendo importante o momento em que isso ocorre. Tais circuitos não precisam de sincronismo algum e são mais simples de serem utilizados.
No entanto, com circuitos muito complexos, como os que são usados nos computadores, máquinas industriais, instrumentos eletrônicos e dispositivos mecatrônicos além de muitos outros casos, o instante em que uma operação deve ser realizada é muito importante, e isso implica que os circuitos devem ser habilitados no instante exato em que determinados níveis lógicos são aplicados em sua entrada.
Isso significa que tais circuitos devem ser sincronizados por algum tipo de sinal vindo de um circuito externo. Este circuito nada mais é do que um oscilador que produz um sinal de clock ou relógio.
Os circuitos que operam com estes sinais são denominados circuitos com lógica sincronizada.
Para os contadores, temos então diversas classificações que levam este fator e outros em conta como, por exemplo:
a) Classificação quanto ao sincronismo:
Os contadores podem ser ASSÍNCRONOS, quando existe o sinal de clock aplicado apenas ao primeiro estágio. Os estágios seguintes utilizam como sinal de sincronismo a saída de cada estágio anterior. Estes contadores também são denominados "Ripple Counters".
O termo inglês é utilizado normalmente, mesmo em documentos em português, como ocorre com muitos outros termos técnicos, conforme já alertamos nossos leitores.
Os contadores também podem ser SÍNCRONOS ou SINCRONIZADOS quando existe um sinal de clock único externo, que é aplicado a todos os estágios ao mesmo tempo.
Na prática, os circuitos dos contadores assíncronos são muito mais simples do que os circuitos dos contadores síncronos. A principal vantagem dos contadores síncronos é que eles podem operar em frequências mais elevadas.
b) Classificação quanto ao modo de contagem
Os contadores podem ser PROGRESSIVOS ou CRESCENTES quando contam numa sequência de números crescentes, ou seja, dos valores mais baixos para os mais altos como (1,2,3,4...). Estes contadores também são conhecidos pelo termo inglês UP COUNTERS.
Os contadores podem ser REGRESSIVOS ou DECRESCENTES quando a contagem é feita dos valores mais altos para os mais baixos como (4,3,2,1...). Esses contadores também são conhecidos pelo termo inglês DOWN COUNTERS.
Se bem que possamos fazer contadores usando funções lógicas comuns e mesmo flip-flops discretos, podemos contar na prática com diversos circuitos integrados, tanto em lógica TTL como CMOS, que já possuem contadores completos implementados.
Alguns circuitos possuem contadores com diversas etapas facilitando, dessa forma, a implementação de projetos digitais que façam a contagem de grande quantidade de pulsos.
O uso de tais circuitos, não só facilita o projeto, como ainda reduz seu custo, e torna-os mais confiáveis pelo menor número de peças usadas.
A seguir, analisaremos o funcionamento dos principais tipos de contadores com que podemos contar para o projeto de circuitos lógicos digitais tanto em lógica TTL como CMOS.
9.2 – Contadores assíncronos
Conforme explicamos, neste tipo de contador, o sinal de clock é aplicado apenas ao primeiro estágio, ficando os demais sincronizados pelos estágios anteriores.
Na figura 35 temos a estrutura básica de um contador deste tipo usando flip-flops do tipo J-K.
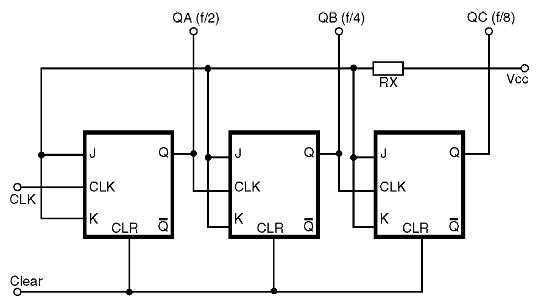
Usamos três estágios ou três flip-flops ligados de tal forma que a saída Q do primeiro serve de clock para o segundo, e a saída Q do segundo serve de clock para o terceiro, e assim por diante, tantos quantos sejam os bits que sejam necessários para representar o número contado.
Sabemos das lições anteriores que os flip-flops ligados da forma indicada funcionam como divisores de frequência. Assim, o sinal de clock aplicado ao primeiro tem sua frequência dividida por 2. A frequência estará dividida por 4 na saída do segundo, e por 8 na saída do terceiro.
Tudo isso pode ser melhor visualizado pelo diagrama de tempos mostrado na figura 36.
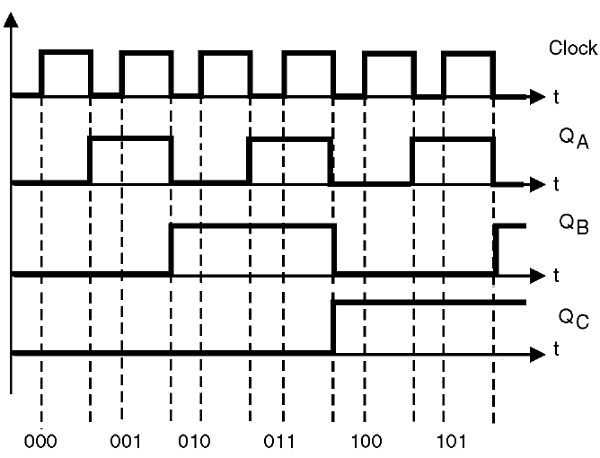
Mas, se elaborarmos uma tabela verdade com os níveis lógicos obtidos na saída de cada um dos flip-flops, a cada pulso do clock aplicado, a partir do instante em que todas as saídas sejam zero, teremos algo interessante a considerar:
| Entrada | QC | QB | QA |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 |
| 4 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 |
| 6 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 |
Veja que a sequência de valores obtidos 000, 001, 010, 011, 100, 101, 110 e 111 corresponde justamente à contagem, em binário, dos pulsos de 0 a 7! Em outras palavras, este circuito conta os pulsos de entrada e fornece saídas que correspondem à representação binária desta contagem.
Veja também que ele faz a contagem crescente, ou seja, de 0 até 7.
É também fácil perceber que, se ao chegarmos no sétimo pulso de entrada, quando os flip-flops estiverem com 111 nas suas saídas, recebendo o oitavo pulso todos os flip-flops zeram, passando as saídas a 000 e começando novamente a contagem.
Se, em lugar de 3 flip-flops, usarmos quatro, no circuito mostrado na figura 37, teremos a contagem de 0000 a 1111, ou seja, uma contagem crescente de 0 a 15 pulsos.
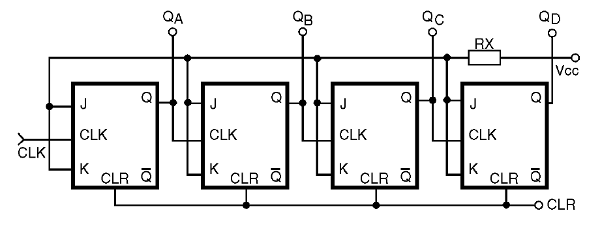
Oito desses flip-flops ligados em série podem contar até 256 pulsos e, com isso, fornecer uma saída de 8 bits ou 1 byte.
Evidentemente, precisaremos de tantos flip-flops quantos sejam os bits necessários à representação do maior número que desejamos contar.
O circuito apresentado comuta na transição negativa do sinal de clock.
Vamos supor agora que, em lugar de usarmos como saídas de contagem as saídas Q de cada flip-flop, usarmos as saídas complementares /Q conforme mostra a figura 38.
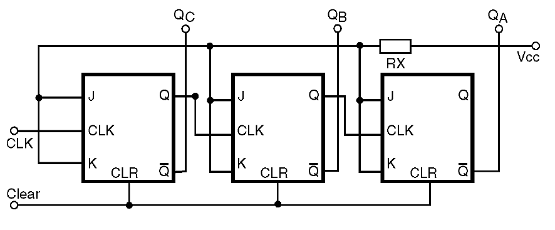
É fácil perceber que, partindo da situação em que todos os flip-flops estejam ressetados o valor inicial correspondente será 000 ou valor binário 7, e a tabela verdade obtida terá nas saída os complementos da tabela anterior. Esta tabela será dada por:
| Entrada | QA | QB | QC | Valor Binário |
| 0 | 1 | 1 | 1 | 7 |
| 1 | 1 | 1 | 0 | 6 |
| 2 | 1 | 0 | 1 | 5 |
| 3 | 1 | 0 | 0 | 4 |
| 4 | 0 | 1 | 1 | 3 |
| 5 | 0 | 1 | 0 | 2 |
| 6 | 0 | 0 | 1 | 1 |
| 7 | 0 | 0 | 0 | 0 |
Esse contador fornece em sua saída valores binários que correspondem à contagem decrescente dos pulsos de entrada, partindo de 7. Trata-se, portanto, de um contador decrescente ou DOWN COUNTER.
Como no caso anterior, se tivermos mais flip-flops podemos contar a partir de valores mais altos. Com 4 flip-flops podemos partir a contagem de 15 e com 8 flip-flops de 255.
Veja que a quantidade máxima que podemos contar, com um contador deste tipo, depende unicamente da quantidade de flip-flops usados.
Este valor pode ser calculado pela fórmula:
n = 2x
Onde n é o valor máximo de contagem
x é o número de estágios ou flip-flops usados
Para x = 4, por exemplo, teremos:
n = 24
n = 2 x 2 x 2 x 2
n = 16
Isso significa que, partindo de zero podemos contar até 15, conforme vimos nos exemplos dados.
Para x = 8 temos:
n = 28
n = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
n = 256
Um problema que ocorre com este tipo de flip-flop é que, cada flip-flop precisa de um certo tempo para mudar de estado. Isso significa que, à medida que usamos mais flip-flops em sequência num contador, os tempos de mudança de estado se somam e o conjunto precisa de cada vez mais tempo para chegar ao estado final desejado.
Se aplicarmos um novo pulso de clock para contagem à entrada do circuito, antes de ocorrer a mudança de estado de todos os flip-flops do conjunto, pode ocorrer um funcionamento errático.
Assim, a frequência máxima de operação de um contador é dada pelo tempo necessário para cada estágio mudar de estado multiplicado pelo número de estágios usados no contador.
Evidentemente, num contador com muitos estágios, o tempo total pode limitar sensivelmente o desempenho esperado.
9.3 – Contagem programada
Conforme vimos, os ciclos de contagem dos circuitos dados como exemplos no item anterior são sempre potências de 2, ou seja, são circuitos que contam até 2, 4, 8, 16, 32, etc.
O que devemos fazer, se precisarmos de um circuito que tenha um ciclo de contagem diferente desses valores, ou seja, que não seja uma potência de 2?
Isso pode ser feito se levarmos em conta dois fatores:
* Podemos usar a entrada CLEAR para reiniciar a contagem (zerando-a) quando ela chegar ao valor desejado. Por exemplo, podemos reiniciar a contagem depois do 5, ou seja, no 6, se quisermos um contador que conte de 0 a 5, ou seja, que tenha 6 estados de saída, conforme mostra a tabela verdade dada a seguir:
| Entrada | QC | QB | QA | |
| 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | |
| 2 | 0 | 1 | 0 | |
| 3 | 0 | 1 | 1 | |
| 4 | 1 | 0 | 0 | |
| 5 | 1 | 0 | 1 | |
| 6 | 0 | 0 | 0 | Estado instável |
No sexto pulso, que corresponde ao estado, 110 o circuito vai a um estado que ativa a entrada CLEAR e leva todos os flip-flops a serem ressetados.
Para este circuito a solução é simples. Veja que a situação em que devemos ter a volta a zero da contagem e, portanto, a ativação da linha CLR (clear) ocorre com uma única combinação de sinais: QA e QB no nível alto.
Se usarmos flip-flops que tenham entradas CLEAR ativadas pelo nível alto, basta agregar ao circuito uma porta AND de duas entradas com as entradas ligadas nas saídas QB e QC do contador, e a saída na linha comum de CLEAR de todos os flip-flops, conforme mostra a figura 39.
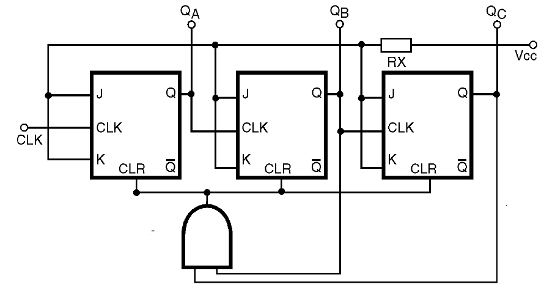
Se os flip-flops usados tiverem um CLEAR ativado no nível baixo, como o 7476 (TTL), basta usar uma porta NAND em lugar de AND.
Se quiséssemos um contador até 4, por exemplo, o estado em que deveria ocorrer a ativação da entrada CLEAR ocorreria com a quinta combinação de saídas, ou seja, 101, o que significa QC = 1 e QA = 1. Bastaria então ligar as entradas da porta AND nessas saídas, conforme mostra a figura 40.
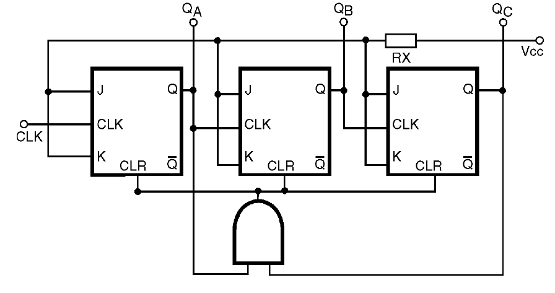
Um diagrama de tempos pode mostrar ao leitor exatamente o que ocorre com o contador elaborado desta maneira. Este diagrama é mostrado na figura 41.
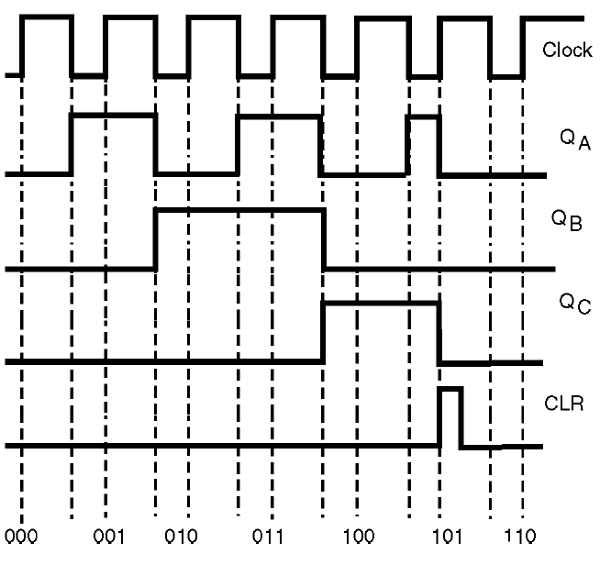
Observe que, quando as saídas chegarem ao estado 110, que seria a contagem do quinto pulso no circuito, conforme mostra a figura 42, um pulso de reset de curta duração é produzido. Esta curta duração é dada justamente pelo tempo que os flip-flops levam para mudar de estado ressetando, pois eles "realimentam" as entradas da porta AND.
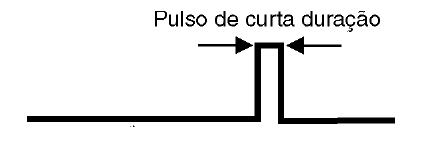
Nos exemplos dados, fizemos a programação da contagem usando as entradas de CLEAR de cada flip-flop.
Outra maneira de projetarmos um contador consiste em usarmos as entradas PRESET em lugar de CLEAR. Para isso, fazemos com que, no momento em que for atingida a contagem do valor imediatamente anterior aquele em que deve ocorrer a volta a zero, ou seja, n-1, em lugar de termos a comutação dos flip-flops, tenhamos a ativação das entradas de PRESET. Desta forma, no pulso seguinte de clock (n) teremos a volta a zero (reset) do contador.
Para um contador de 6 estados, que depois do quinto pulso resseta, teremos a seguinte tabela verdade.
| Pulsos | QC | QB | QA | |
| 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | |
| 2 | 0 | 1 | 0 | |
| 3 | 0 | 1 | 1 | |
| 4 | 1 | 0 | 0 | |
| 5 | 1 | 0 | 1 | o Preset, ativado |
| x | x | x | x | Volta a zero na transição do clock |
| 6 | 0 | 0 | 0 | |
| 7 | 0 | 0 | 1 | |
| 8 | 0 | 1 | 0 | |
| etc. |
Um circuito usando uma porta AND é mostrado na figura 43.
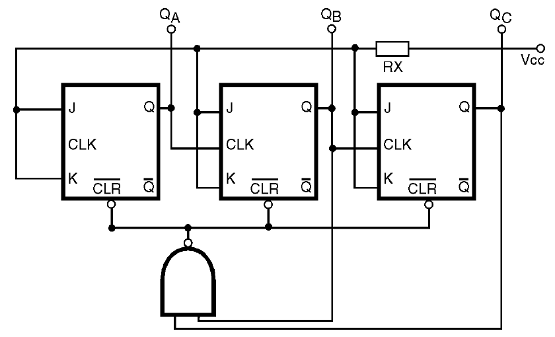
Veja que a detecção da condição de produção do pulso de PRESET deve ser reconhecida com os níveis 101 nas saídas dos estágios dos contadores, e com o pulso indo ao nível alto na entrada de contagem.
Para obtermos a configuração 1111, que nos permitiria usar uma porta AND de quatro entradas, basta levar em conta a saída /QB em lugar de QB.
Assim, basta usar a porta AND e ligá-la nas entradas de PRESET (PR) dos flip-flops.
Se as entradas forem ativadas no nível baixo (/PR) basta trocar a porta AND por uma porta NAND de quatro entradas.
9.4 – Contadores Up/DFown (Progressivos e Regressivos)
Usando alguns artifícios, por exemplo, portas lógicas apropriadas, podemos programar um contador de modo que ele possa tanto contar progressivamente como regressivamente.
Esses artifícios são encontrados já embutidos em alguns circuitos integrados que tanto podem ser usados para contagem progressiva como regressiva, dependendo apenas da programação feita por um pino externo.
Usando 3 estágios, por exemplo, podemos ter um contador UP/DOWN conforme mostra a figura 44.
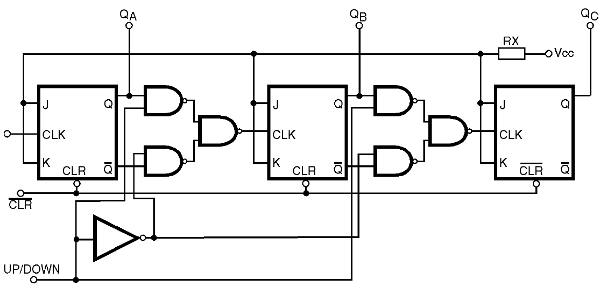
Uma entrada (UP/DOWN) pode ser usada para determinar o sentido da contagem. Trata-se de uma entrada seletora de dados ou DATA SELECTOR, que pode ser usada para mudar o modo de funcionando dos estágios deste circuito.
O funcionamento deste circuito é simples de explicar. Conforme vimos nesta lição, se usarmos as saídas Q dos flip-flops de um contador, a contagem será crescente, mas se usarmos as saídas /Q a contagem será decrescente.
Assim, o que fazemos é colocar um circuito seletor nessas saídas, de tal modo que ele coloca a saída Q de cada flip-flop na entrada de clock do seguinte quando a contagem deve ser progressiva, mas coloca a saída /Q na entrada do seguinte quando a contagem deve ser decrescente. Três portas NAND para cada estágio podem fazer isso a partir do sinal de comando UP/DOWN.
9.5 – Contadores síncronos
Sincronizar a contagem por um clock único, aplicado a todos os estágios, não é apenas uma necessidade dos circuitos mais complexos, mas também os eu envolve lógica mais elaborada, principalmente os usados em informática, automação e instrumentação. O sincronismo de todos os estágios pelo mesmo clock tem ainda vantagens operacionais importantes.
Conforme vimos, nos contadores assíncronos, os tempos de comutação de cada flip-flop influem no funcionamento final do circuito, pois eles são cumulativos. Em outras palavras, cada estágio precisa esperar o anterior completar a operação antes de iniciar a sua.
Usando lógica sincronizada, ou seja, um contador em que todos os estágios são sincronizados por um clock único, este problema não existe e podemos ter contadores muito mais rápidos, na verdade contadores cuja velocidade independe do número de etapas.
Para mostrar como isso pode ser feito vamos tomar como exemplo o circuito da figura 45.
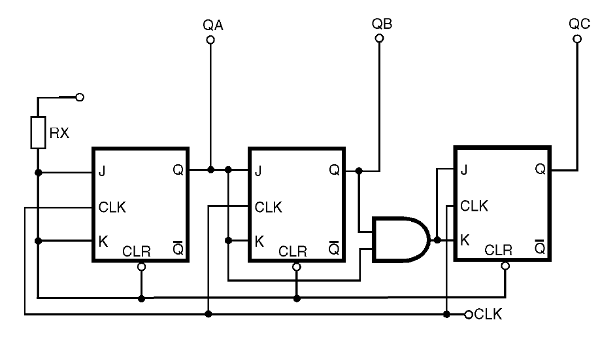
Este circuito utiliza flip-flops tipo J-K ligados de uma forma denominada PARALLEL CARRY.
O termo "carry" se refere ao "vai um" ou "transporta" e é muito usado, sendo mantido o original em inglês na maioria da documentação de eletrônica digital em português.
Nesta forma de ligação, J e K do primeiro flip-flop são mantidas no nível alto com a ajuda de um resistor ligado ao positivo da alimentação (Vcc). Desta forma, o primeiro flip-flop muda de estado a cada pulso de clock.
No entanto, J do segundo flip-flop está ligado à saída Q do primeiro. Isso significa que o segundo flip-flop só mudará de estado quando o primeiro flip-flop for ressetado, ou seja, a cada dois pulsos de clock.
Da mesma forma, com o uso de uma porta AND o terceiro flip-flop só vai mudar de estado quando as saídas Q do primeiro e segundo flip-flop forem ao nível 1, ou seja, a cada 4 pulsos de clock.
Para 4 bits, utilizando 4 estágios, podemos usar o circuito mostrado na figura 46.
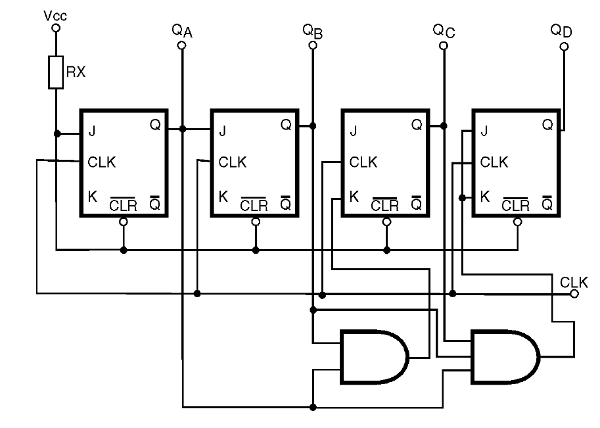
Um problema que ocorre com este tipo de configuração é que, a partir de 3 estágios, a cada estágio que acrescentamos no contador, devemos colocar uma porta AND adicional, cujo número de entradas vai aumentando. Assim, para 4 estágios a porta deve ter três entradas, para 5 estágios a porta deve ter 4 entradas e assim por diante.
Uma maneira de evitarmos este problema consiste em usar uma configuração diferente de contador que está ilustrada na figura 47 e que é denominada RIPPLE CARRY.
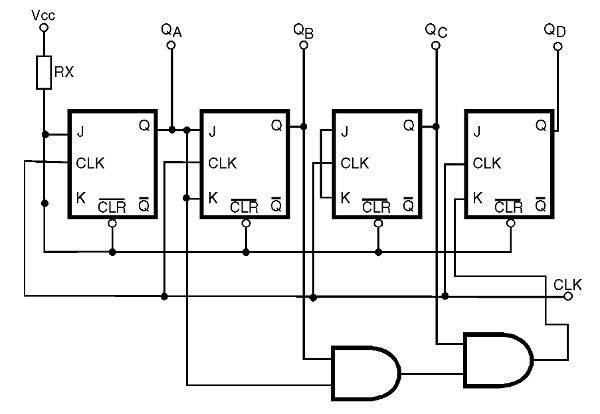
Lembramos que a palavra "ripple" significa ondulação ou variação, e também é mantida na forma original, quando trabalhamos com eletrônica digital.
Neste circuito as portas usadas sempre precisam ter apenas duas entradas, o que é importante para a implementação prática do contador. No entanto, como desvantagem deste circuito temos uma limitação da velocidade de operação, pois como o sinal para cada estágio vem da porta anterior temos de considerar seu atraso.
9.6 – Contadores síncronos programáveis
Da mesma forma que no caso dos contadores assíncronos, também é necessário, em determinadas aplicações, fazer a contagem até valores que não sejam potências de 2.
A divisão ou contagem por outros valores pode ser feita com a ajuda de portas que são ligadas de modo a "sentir" quando um determinado valor é alcançado e então ressetando todos os flip-flops.
A técnica é exatamente a mesma que vimos para o caso dos contadores assíncronos, utilizando portas e outras funções lógicas mais simples.
Também é importante saber que existem circuitos integrados, tanto das famílias TTL e subfamílias como CMOS que já contém recursos para a contagem até valores que não sejam potências de 2 ou então que possam ser utilizados nessa função com poucas portas externas..
Mais adiante, quando dermos circuitos práticos com flip-flops TTL e CMOS teremos diversos tipos de divisores usando circuitos integrados comuns.
9.7 – Contadores TTL
Utilizando portas lógicas e flip-flops, podemos implementar contadores que contem até qualquer valor, ou façam a divisão de um sinal de entrada por qualquer número inteiro. No entanto, na prática podemos contar com muitos circuitos integrados em tecnologia TTL que já contém estes circuitos completos num único chip, e até com recursos que permitam alterar seu funcionamento de modo a se obter a contagem até um determinado valor previamente programado.
O uso destes circuitos, que podem ser ligados em conjunto (em cascata), permite a contagem até praticamente qualquer valor inteiro com um mínimo de componentes externos e alcançando velocidades bastante altas.
A seguir, veremos alguns dos principais circuitos integrados contadores em tecnologia TTL.
Esses contadores tanto podem ser obtidos na família standard como também em suas diversas subfamílias.
7490 - Contador de Década
O circuito integrado 7490 é um dos mais populares de todos os contadores TTL, contendo em seu interior quatro flip-flops já interligados de modo a funcionar como divisores por 2 e por 5. Isso significa que esses divisores podem ser usados de modo a se ter um contador até 2 e um contador até 5, e em conjunto, como um contador até 10.
Na figura 48 temos a disposição dos terminais deste circuito integrado.
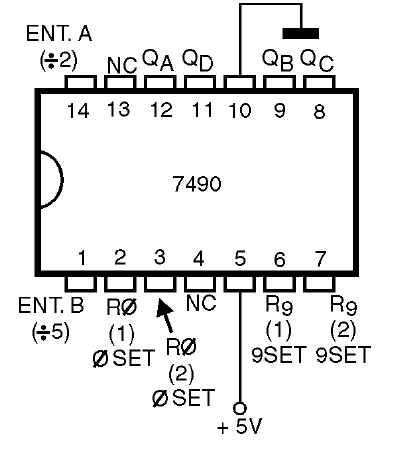
O circuito integrado 7490 pode ser usado de três formas diferentes, sempre com as entradas R0(1), R0(2), R9(1) e R9(2) aterradas:
* Quando ligamos a entrada B à saída QA e aplicamos o sinal de clock à entrada A, o circuito funciona como um contador BCD, ou seja, conta até 10, com as saídas decimais codificadas em binário apresentadas nos pinos QA, QB, QC e QD. Esta ligação é mostrada na figura 49.
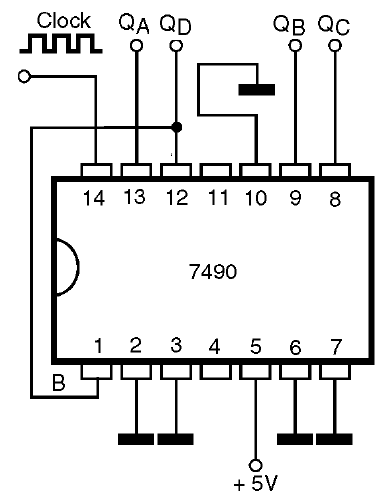
A tabela verdade para os pulsos aplicados na entrada neste modo de funcionamento será:
| Pulso | QD | QC | QB | QA |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
Observe que a saída QA é a de menor peso (2) e a saída QD é a de maior peso (8).
* Quando ligamos a saída QD à entrada A e aplicamos o sinal de clock a entrada B, teremos o circuito funcionando como um divisor de frequência por 10 simétrico. Teremos na saída AQ um sinal quadrado (ciclo ativo de 50%) com 1/10 da frequência do clock. Este modo de funcionamento tem as ligações mostradas na figura 50.
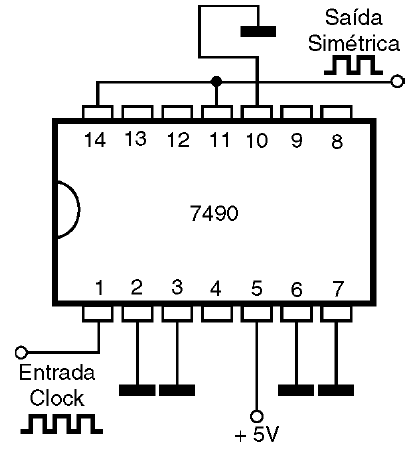
* Finalmente, quando quisermos usar o circuito como divisor por 2 ou por 5, com setores independentes, não é preciso ligação externa alguma.
O sinal aplicado em CLK1 tem a frequência dividida por 2, e o sinal aplicado no CLK2 tem a frequência dividida por 5. Na operação normal as entradas R0(1) e R0(2) devem ser mantidas no nível baixo.
Para a série normal ou standard a frequência máxima de clock é 18 MHz, e cada circuito integrado consome uma corrente média de 32 mA.
Para zerar a contagem, basta levar as entradas 0SET ao nível alto por um instante.
Como o contador é do tipo "ripple, mudando de estado com a fronte negativa do sinal de clock, é preciso que o sinal usado para sua excitação seja livre de qualquer repique.
7492 – Contador-Divisor por 12
Este circuito integrado contém quatro flip-flops ligados como um divisor por 2, e um divisor por 6. Os dois divisores podem ser usados de maneira independente. A pinagem deste circuito integrado TTL é mostrada na figura 51.
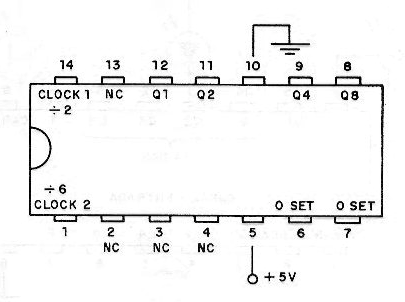
O disparo dos flip-flops ocorre na transição do sinal de clock do nível alto para o nível baixo (fronte negativa do sinal de entrada). Para ressetar o contador para 0000, basta aplicar o nível lógico 1 nas entradas 0 SET.
Existem três modos de operação para este circuito integrado:
* Como contador até 12, basta ligar a saída QA à entrada B. O sinal de clock é aplicado à entrada A. A tabela verdade para este modo de operação será:
| Entrada | QD | QC | QB | QA |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 1 |
No décimo segundo pulso, o circuito resseta e volta à saída 0000.
Na segunda forma de operação ligamos a saída QD à entrada A. O circuito funcionará como um divisor simétrico de frequência. A frequência do sinal de clock aplicado a entrada B será dividida por 12 e o sinal terá um ciclo ativo de 50%.
Na operação sem nenhuma ligação externa, o sinal aplicado à entrada A terá sua frequência dividida por 2 e o sinal aplicado na entrada B terá sua frequência dividida por 6.
A frequência máxima de operação do 7492 da série normal (standard) é de 18 MHz e o consumo por CI é da ordem de 31 mA.
7493 - CONTADOR BINÁRIO DE 4 BITS
Neste circuito integrado encontramos 4 flip-flops que formam um divisor por 2 e um divisor por 8. Em conjunto, eles podem dividir ou contar até 16, fornecendo uma saída de 4 bits completa.
Na figura 52 temos a pinagem deste circuito integrado.
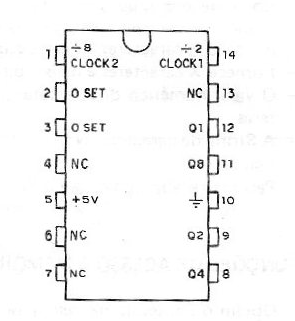
Na operação normal as entradas 0 SET (2) e ) SET (3) são mantidas no nível baixo e o disparo ocorre com a transição do sinal de clock do nível alto para o nível baixo.
A operação pode ocorrer de dois modos:
Com a saída Q1 ligada à entrada 14 e o sinal de entrada aplicado na entrada 1 o circuito conta na sequência normal de 0000 até 1111 e nas saídas Q1, Q2, Q3 e Q4 teremos os valores correspondentes.
Sem conexões externas, podemos usar o circuito como divisor por 2 e por 8 independentes, aplicando os sinais nas entradas A e B respectivamente.
74190 – Contador/divisor por 10 Up/Down
Trata-se da versão do 74190 que conta no sentido progressivo e regressivo. A pinagem deste circuito integrado é mostrada na figura 53.
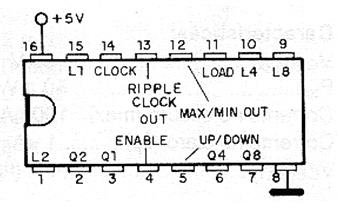
Na operação normal progressiva, a entrada LOAD (carga) deve ser mantida no nível alto, a habilitação (EN) no nível baixo e a entrada UP/DOWN deve ser mantida no nível baixo. Com esta entrada no nível alto ele conta regressivamente.
O contador avança uma unidade na contagem na transição do nível baixo para o nível alto do pulso de clock.
A frequência máxima de contagem para a versão standard é 20 MHz e o consumo médio por circuito integrado é 65 mA.
9.8 – Contadores e divisores CMOS
Também podemos contar com diversos circuitos integrados em tecnologia CMOS contendo contadores e divisores. A seguir veremos alguns dos mais importantes.
4017 – Contador/divisor por 10
Este circuito integrado contém um conjunto de flip-flops e um sistema decodificador para as saídas que fornecem sinais do tipo 1 de 10.
Neste tipo de saída, a cada pulso apenas uma saída vai ao nível alto, voltando a anterior ao nível baixo. Assim, para 10 pulsos de entrada, as saídas passam sequencialmente ao nível alto.
Na figura 54 temos a pinagem deste circuito integrado.
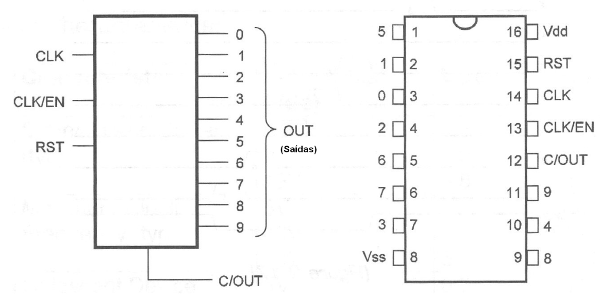
Na operação normal, contando até 10, as entradas RST e EN devem ser mantidas no nível baixo. Levando-se a entrada RST ao nível alto o contador é ressetado. Se a entrada EN for levada ao nível alto a contagem é paralisada.
Na figura 55 temos as formas de onda deste contador, mostrando como em cada instante temos sempre apenas uma saída no nível alto.
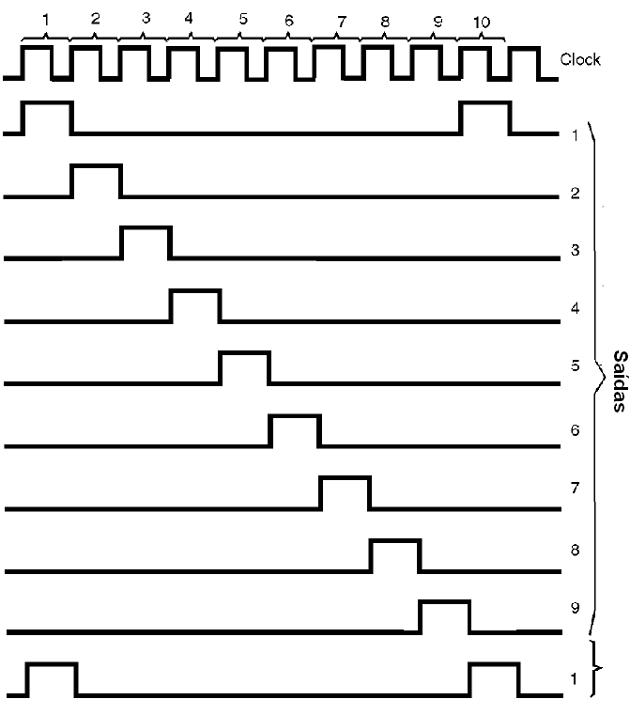
Como em todos os circuitos CMOS, a frequência máxima de contagem depende da tensão de alimentação. A tabela abaixo fornece as características desse CI:
|
Característica |
Condições (Vdd) |
Valor |
|
Corrente de saída drenada/fornecida tip. |
5 V 10 V 15 V |
0,88 mA 2,25 mA 8,8 mA |
|
Frequência máxima de clock (tip) |
5 V 10 V 15 V |
2 MHz 5 MHz 6 MHz |
|
Corrente quiescente máxima |
5 V 10 V 15 V |
0,3 mA 0,5 mA 1,0 mA |
|
Faixa de tensões de alimentação |
3 V a 15 V |
4018 - Contador/Divisor Por N
Este circuito integrado pode fazer a divisão ou contagem de pulsos em valores até 10 programados pelas ligações externas.
Sua pinagem é mostrada na figura 56.
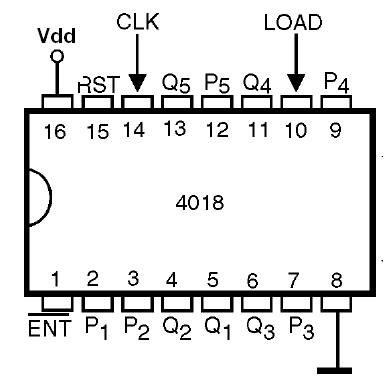
Seu funcionamento será detalhado no próximo capítulo como base dos contadores mais complexos.
Suas principais características são dadas na tabela seguinte:
|
Característica |
Condições (Vdd) |
Valor |
|
Corrente drenada/fornecida (tip) |
5 V 10 V 15 V |
0,88 mA 2,25 mA 8,8 mA |
|
Frequência máxima de clock |
5 V 10 V 15 V |
4 MHz 9 MHz 14 MHz |
|
Corrente quiescente máxima |
5 V 10 V 15 V |
0,3 mA 0,5 mA 1,0 mA |
|
Faixa de tensões de alimentação |
3 V a 15 V |
Índice
Curso de Eletrônica Digital – Analógica e Digital – Sistemas de Numeração (CUR5001)
Curso de Eletrônica Digital – A Álgebra de Boole (CUR5002)
Curso de Eletrônica Digital – Famílias de Circuitos Lógicos Digitais (CUR5003)
Curso de Eletrônica - Eletrônica Digital – A Família de Circuitos Integrados CMOS (CUR5004)
Curso de Eletrônica Digital – Combinando Funções Lógicas - (Lógica Combinacional) (CUR5005)
Curso de Eletrônica - Eletrônica Digital - Os Elementos Biestáveis (CUR5006)
Curso de Eletrônica - Eletrônica Digital - Flip-Flops e Funções Integradas em CIs (CUR5007)
Curso de Eletrônica - Eletrônica Digital - Os Multivibradores Astáveis e Monoestáveis (CUR5008)
Curso de Eletrônica - Eletrônica Digital - Os Contadores Digitais (CUR5009)
Curso de Eletrônica - Eletrônica Digital - Memórias, ADCs e DACs (CUR5013)


















