As tabelas verdade
Os diversos sinais de entrada aplicados a uma função lógica, com todas as suas combinações possíveis, e a saída correspondente, podem ser colocados numa tabela. Já tivemos uma noção disso nas primeiras lições.
Nas colunas de entradas colocamos todas as combinações possíveis de níveis lógicos que as entradas podem assumir. Na coluna correspondente à saída colocamos os valores que esta saída assume em função dos níveis lógicos correspondentes na entrada.
Essa tabela, conforme já vimos, é chamada "tabela verdade" ou "truth table", se adotarmos o termo em inglês.
Estudamos, desta forma, que a tabela verdade para uma função AND de duas entradas será representada conforme mostra a figura 121.
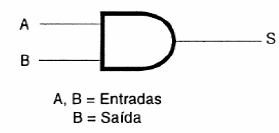
A B S
0 0 0
0 1 0
1 0 0
1 1 1
Veja que nas colunas de entrada (A e B), para termos todas as combinações possíveis, fazemos o equivalente a uma contagem binária de 0 a 3, já que:
00 = 0
01 = 1
10 = 2
11 = 3
Para uma tabela verdade feita para uma porta AND de 3 entradas teremos:
A B C S
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
Neste caso, as combinações de níveis lógicos na entrada, na realidade, correspondem à uma contagem binária de 0 a 7 já que:
000 = 0
001 = 1
010 = 2
011 = 3
100 = 4
101 = 5
110 = 6
111 = 7
Observe então que, para uma função de 2 entradas, temos 4 combinações possíveis de sinais de entrada. Para uma função de 3 entradas, teremos 8 combinações e para uma função de 4 entradas, 16 combinações e assim por diante.
O conhecimento da contagem binária facilita bastante a elaboração de tabelas verdade quando todas as combinações possíveis de níveis lógicos em 2, 3 ou 4 entradas devam ser analisadas.
Assim, uma vez que o leitor conheça o comportamento das principais funções, sabendo o que ocorre na saída de cada uma, quando temos determinadas entradas e sabendo elaborar tabelas verdade, fica fácil combinar funções e saber o que acontece em suas saídas.
Na verdade, o ponto principal das informações técnicas dos circuitos lógicos digitais é a sua tabela verdade.
Também, devemos observar que, além das combinações dos níveis lógicos das entradas, também podemos encontrar colunas que levam em conta os níveis lógicos de entradas especiais como, por exemplo, uma entrada de habilitação (EN), uma entrada que leve o dispositivo a um terceiro estado ou ainda que cause uma transição do nível de sinal.
Nesse caso, como já vimos, independentemente do que ocorra nas entradas, a saída estará num estado de alta impedância. As tabelas verdade podem incluir este terceiro estado do dispositivo.
5.2 - Lógica Combinacional
Denominamos "lógica combinacional" a lógica que rege o funcionamento de diversas funções mais simples quando elas são combinadas, ou reunidas num circuito mais complexo.
Para entender como ela funciona, vamos partir de um exemplo simples de lógica combinacional usando tabelas verdade para saber, por exemplo, o que ocorre na sua saída, com o circuito da figura 122.
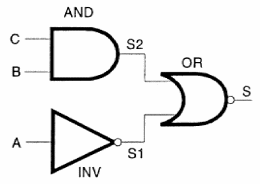
Este circuito faz uso de uma porta AND, um inversor e uma porta OR. O resultado desta configuração é uma função combinacional que tem três entradas e uma saída.
Para elaborar a tabela verdade para este circuito, e assim determinarmos todas as saídas possíveis em função das entradas, devemos levar em conta que ele é formado por duas etapas.
Na primeira etapa temos a porta AND e o inversor, enquanto que na segunda etapa temos a porta OR. Isso significa que as saídas dos circuitos da primeira etapa, que chamaremos de S1 e S2, são as entradas da segunda etapa.
Temos então de levar em conta estas saídas na elaboração da tabela verdade que terá no seu topo as seguintes variáveis:
| A | B | C | S1 | S2 | S |
A, B e C são as entradas dos circuitos. S1 e S2 são pontos intermediários do circuito, ou saídas intermediárias, que precisam ser analisadas para se obter S que é a saída final do circuito.
Começamos por colocar em A, B e C todas as suas condições possíveis, ou todas as combinações de níveis lógicos que podem ser aplicadas ao circuito:
| A | B | C | S1 | S2 | S |
| 0 | 0 | 0 | |||
| 0 | 0 | 1 | |||
| 0 | 1 | 0 | |||
| 0 | 1 | 1 | |||
| 1 | 0 | 0 | |||
| 1 | 0 | 1 | |||
| 1 | 1 | 0 | |||
| 1 | 1 | 1 |
Veja que, como temos 3 entradas, as combinações possíveis para os níveis lógicos de entrada são 8. Os níveis aplicados equivalem, portanto, à contagem binária de 0 a 7.
O passo seguinte é colocar os valores possíveis de S1 que correspondem à saída do inversor. Sabemos que a tabela verdade para o inversor é:
A | S
0 | 1
1 | 0
Ora, como no nosso caso A é a entrada do inversor, e S1 é sua saída, podemos partir para a determinação de toda a coluna S1 simplesmente invertendo os valores da coluna A, da seguinte forma:
| A | B | C | S1 | S2 | S |
| 0 | 0 | 0 | 1 | ||
| 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 1 | ||
| 0 | 1 | 1 | 1 | ||
| 1 | 0 | 0 | 0 | ||
| 1 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 0 | ||
| 1 | 1 | 1 | 0 |
Para encontrar os valores da coluna S2, observamos que ela corresponde à tabela verdade da função AND, onde as entradas correspondentes são B e C e a saída é S2. Aplicamos, portanto, a função AND de entradas B e C, colocando os resultados na coluna S2.
| B | C | S2 |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Como temos duas entradas, os resultados obtidos são 4, mas observamos que na tabela principal, as quatro combinações de entrada são repetidas duas vezes.
Temos então:
| A | B | C | S1 | S2 | S |
| 0 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 1 |
Finalmente, levando em conta que S1 e S2 são entradas de uma porta OR de duas entradas, cuja saída é S e tem por tabela verdade a mostrada abaixo, podemos elaborar a coluna final de saídas (S)
| S1 | S2 | S |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Nesse caso, também, a combinação de 4 entradas é repetida duas vezes.
A tabela final fica então:
| A | B | C | S1 | S2 | S |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 |
Trata-se de uma função bastante interessante que pode ser definida como "a que fornece uma saída alta somente quando a entrada A estiver no nível baixo, não importando as demais entradas ou ainda quando as três entradas estiverem no nível alto".
Evidentemente, não sabemos em que aplicação prática o leitor pode precisar de tal função, mas fica o exemplo de como ela pode ser obtida e como podemos prever o seu funcionamento para todas as entradas possíveis, usando tabelas verdade.
5.3 - Como Projetar Um Circuito Combinacional
O problema de se saber o que acontece com a saída de um circuito formado por muitas funções lógicas, quando suas entradas recebem diversas combinações de sinais, não é o mais importante para o projetista de equipamentos digitais.
Na verdade, muito mais importante que este procedimento é justamente fazer o contrário, ou seja, projetar um circuito que, em função de determinados sinais de entrada forneça exatamente na saída o que se deseja.
O projeto de um circuito que tenha uma determinada função envolve um procedimento de síntese em algumas etapas.
Na primeira etapa deve ser definido o problema, estabelecendo-se exatamente qual é a função a ser executada, ou seja, quais as entradas e quais as saídas.
Numa segunda etapa coloca-se o problema numa tabela verdade ou ainda na forma de equações lógicas. O procedimento que abordaremos neste curso será basicamente o da obtenção das funções a partir das tabelas verdade e das equações lógicas.
Finalmente numa terceira etapa obtemos o circuito que exerça as funções desejadas.
Na terceira etapa, temos um ponto importante a ser considerado que consiste na minimização do circuito, já que na maioria dos casos pode-se implementar a mesma função de muitas formas diferentes como atesta o circuito simples mostrado na figura 123.
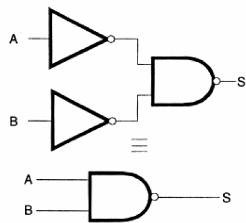
Veja que podemos ter o mesmo circuito com quantidades de portas diferentes, o que significa que na prática deve-se levar este fato em conta.
Não é apenas o número de portas que determinará a configuração final, mas sim seu custo e a eventual utilização em outras partes do circuito.
Por exemplo, se o circuito já estiver usando dois inversores dos seis disponíveis num circuito integrado e a nossa função tiver uma solução um pouco maior, mas que use estes inversores será interessante adotá-la para aproveitar os inversores ociosos.
Outro ponto a ser considerado é que hoje existem circuitos lógicos digitais que consistem em funções numa certa quantidade e que podem ser interligadas por programação.
Assim, um mesmo circuito, só precisa ser programado de determinada forma para exercer as funções desejadas, interligando-se, através desse programa as portas que vão ser usadas.
A seguir daremos um exemplo de como podemos obter os circuitos a partir de uma tabela verdade.
Pedimos ao leitor especial atenção para esses procedimentos, que apesar de simples exigem cuidados, pois eles consistem numa poderosa ferramenta de trabalho para o projetista de circuitos digitais.
a) Passo 1 - Determinação das equações lógicas
Lembramos que para as funções estudadas temos as seguintes representações:
* Função E (AND)
Y=A.B
* Função Não-E (NAND)
Y = /(A.B)
* Função OU (OR)
Y=A+B
* Função Não-OU (NOR)
Y = /(A+B)
* Função Não (NOT) ou inversor
Y = /A
* Função ou exclusivo (Exclusive OR)
Y=A(+)B
a) Eletrônica
a + a = a
a x a = a
b) Notação Matemática (Teoria dos Conjuntos)
a u a = a
a ∩ a = a
c) Lógica
a v a = a
a Λ a = a
Vamos tomar como exemplo a tabela verdade abaixo para se determinar a função lógica correspondente:
| A | B | C | Y | LINHA |
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 2 |
| 0 | 1 | 0 | 1 | 3 |
| 1 | 1 | 0 | 0 | 4 |
| 0 | 0 | 1 | 1 | 5 |
| 1 | 0 | 1 | 0 | 6 |
| 0 | 1 | 1 | 0 | 7 |
| 1 | 1 | 1 | 1 | 8 |
Nesse exemplo, A, B e C são as entradas e Y a saída.
Indicamos os números das linhas na última coluna de modo a facilitar as explicações que daremos a seguir.
Conforme podemos ver temos saídas no nível 0 para as linhas 0, 3, 5 e 6 enquanto que para as linhas 1, 2. 4 e 7 temos saída 1.
Isso quer dizer que teremos a função OU para as linhas cuja saída é 1 podem ser encaradas como operações OR com tabelas que teriam 1 na saída apenas nas linhas 1, 2, 4 e 7, conforme mostrado a seguir:
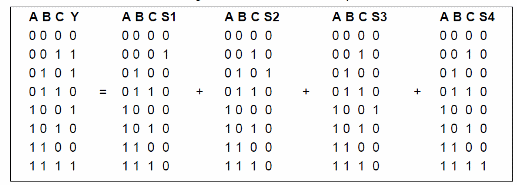
Isso nos permite escrever as equações lógicas para cada uma das quatro tabelas da seguinte forma:
S1 = /A . /B . C que corresponde a A = 0, B = 0 e C = 1
S2 = /A . B . C que corresponde a A = 0, B = 1 e A = 0
S3 = /A . /B . C que corresponde a A = 1, B = 0 e C = 0
S4 = A . B . C que corresponde a A = 1, B = 1 e C = 1
Como a saída S é a combinação das quatro funções temos:
S = S1 + S2 + S3 + S4
Substituindo pelos valores encontrados temos:
S = /A./B.C + /A.B.C + /A./B.C + A.B.C
Esta é então a função lógica que representa a tabela verdade que propusemos como parte inicial do problema e para a qual devemos encontrar um circuito equivalente.
Passo 2 - Implementação dos Circuitos Combinacionais
Conforme estudamos em lições anteriores, é possível usar as portas NAND e NOR como blocos lógicos universais a partir dos quais é possível elaborar qualquer outra função ou mesmo funções mais complexas.
É por esse motivo que os circuitos integrados que contém essas funções são os mais comuns em todas as famílias lógicas.
Para exemplificar como isso pode ser feito, vamos tomar como exemplo uma função um pouco mais simples do que aquela que obtivemos no passo anterior.
Tomemos como exemplo a expressão:
S = A . B . /C + /A . /B . C
Podemos tentar implementá-la usando portas NAND, e eventualmente inversores, já que a barra sobre cada letra indica sua negativa, conforme já estudamos.
A operação (.) pode ser realizada utilizando-se uma porta NAND que ligada a um inversor nos fornece uma porta AND.
Assim, conforme mostra a figura 124 podemos implementar A.B.C usando uma porta NAND de 3 entradas e um inversor.
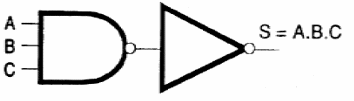
A operação A.B.C pode ser implementada conforme mostra a figura 125.
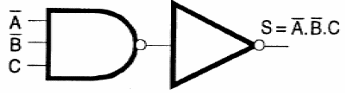
A soma (+) pode ser implementada com uma porta AND ligada a dois inversores conforme mostra a figura 126.
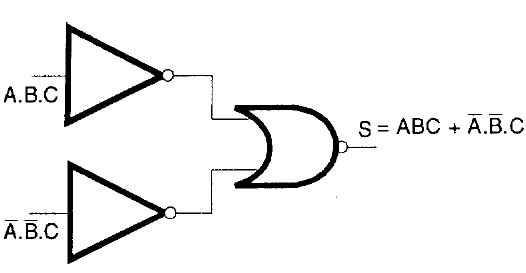
Combinando os três circuitos podemos chegar à configuração final desejada, mostrada na figura 127.
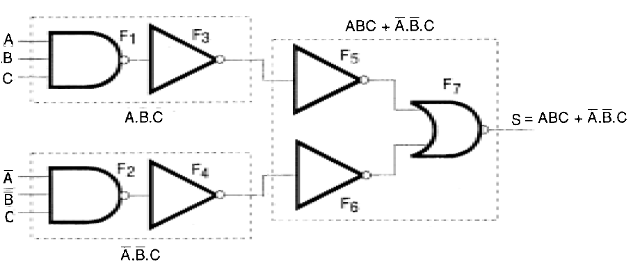
Veja que a inversão da inversão usada no circuito interior nos leva ao circuito original. Isso significa que podemos simplificar a configuração, eliminando as duplas inversões em série.
Isso nos leva à configuração final do circuito mostrada na figura 128.
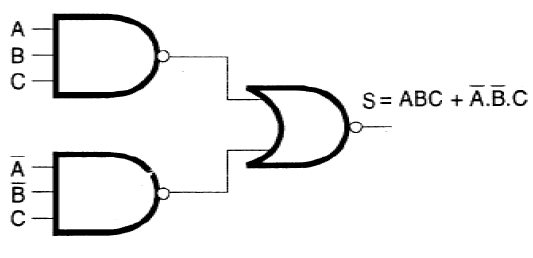
Veja ainda que quando temos uma expressão formada pela soma de produtos, podemos usar portas NAND sem a necessidade de inversores, bastando apenas lembrar duas propriedades:
As combinações de entrada podem ser aplicadas à portas NAND.
As saídas das portas NAND podem ser aplicadas à entrada de uma segunda porta NAND obtendo-se na saída a função desejada.
Vamos agora fazer uma tentativa para implementar uma função usando portas NOR, o que será escolhido quando tivermos um produto de somas.
Tomemos como exemplo a função:
S = (/A + /B + C) . (A + /B + C)
As somas podem ser obtidas facilmente a partir de portas NOR com as saída aplicadas a um inversor. A negação de NOR é OR. O circuito equivalente para três entradas é mostrado na figura 129.
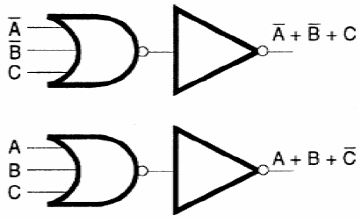
O produto das duas somas é obtido com dois inversores, aplicando os sinais a outra porta OR, ou seja, a outra configuração NOR.
Como nas duas linhas de sinais temos inversores em série, e como o inverso do inverso de um nível lógico é ele mesmo, podemos simplificar o circuito eliminando todos os inversores.
Isso nos permite chegar à configuração final que é mostrada na figura 130.
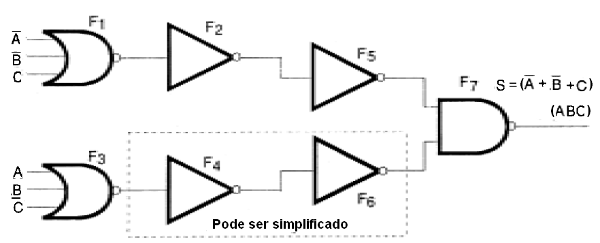
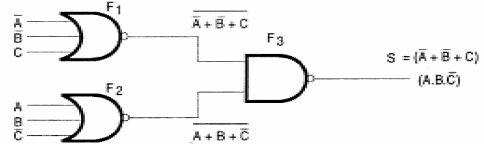
Assim, se quisermos implementar uma função que consiste num produto de somas, basta seguir dois procedimentos básicos:
Aplicar as entradas correspondentes a cada soma a uma porta OR que pode ser obtida associando-se uma porta NOR a um inversor.
Aplicar as saídas obtidas nas funções que devem ser multiplicadas a inversores que são ligados às entradas de uma porta OR final, também obtida com a associação de um inversor a uma porta NOR.
Como os inversores em série se anulam, eles podem ser eliminados e o circuito pode ser implementado utilizando-se apenas portas NOR.
Veja o leitor que podemos resolver o problema de implementar circuitos combinacionais, reduzindo as funções a produtos de somas ou ainda a soma de produtos, casos em que podemos trabalhar com funções NAND ou NOR, conforme mostra a figura 131.
Como as duas soluções levam aos mesmos resultados, num projeto prático, é interessante analisar as configurações obtidas para um problema nos dois casos. Adota-se então a solução que utilizar menos circuitos, ou ainda que for mais conveniente, por exemplo, aproveitando portas ociosas de um circuito integrado já utilizado no mesmo projeto com outras finalidades.
Evidentemente, ao se utilizar as portas contidas nos circuitos integrados reais, o leitor deve estar atento às características elétricas, além de outras.
O que vimos, portanto, é apenas um exemplo do modo como podemos proceder para implementar funções complexas usando portas.
O grau de complexidade dessas funções pode aumentar muito, caso em que o trabalho "manual" descrito se torna difícil. Existem softwares que ajudam a projetar tais circuitos, os quais devem ser procurados para os que pretendem fazer tais tipos de projetos.
5.4 – Simplificando e Minimizando
Uma consequência da possibilidade de se construir funções complexas a partir de portas básicas como OR e AND (OU e E), é poder otimizar um projeto aproveitando-se poucos tipos de circuitos integrados básicos.
Assim, se tivermos uma função que seja obtida utilizando-se portas AND e OR como a mostrada na figura 133, ela tem o inconveniente de precisar de dois tipos diferentes de circuitos integrados.
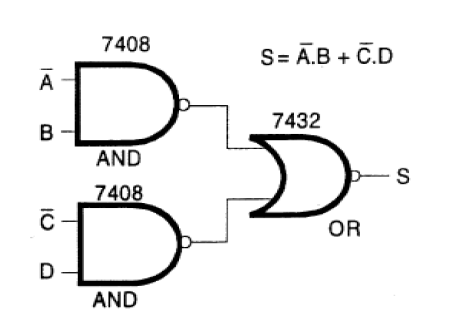
Se quisermos esta função com circuitos TTL, por exemplo, aproveitaremos três das três portas de 3 entradas de um circuito 7411, e também precisaremos aproveitar uma das quatro portas OR de duas entradas de um circuito integrado 7432.
Evidentemente, estaremos usando dois circuitos integrados desperdiçando 1/3 de um e 3/4 do outro.
Podemos simplificar consideravelmente este circuito se usarmos apenas portas NAND com a configuração equivalente mostrada na figura 134.
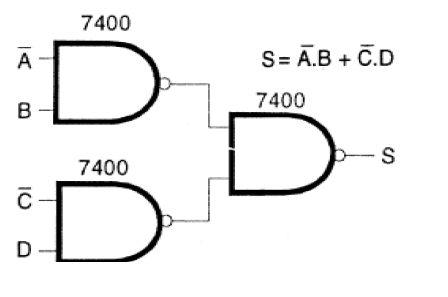
Esse circuito, que tem a mesma função do anterior, usa as três portas de um circuito integrado 7410. O resultado final é que usamos apenas um circuito integrado, que é totalmente aproveitado, sem nenhuma parte ociosa.
Veja que é importante considerar essa possibilidade num projeto comercial onde o número de componentes, e o seu custo, são fatores importantes para sua implementação.
5.5 – Diagramas de Karnaugh
Um processo bastante interessante de se representar uma tabela verdade, e a partir dela se obter uma simplificação dos circuitos utilizados para sua implementação, é o que faz uso dos chamados diagramas ou mapas de Karnaugh.
O diagrama de Karnaugh consiste numa tabela retangular com número de quadros que corresponde a 2 elevado ao expoente N, onde N é o número de variáveis do circuito.
Cada variável lógica ocupa no gráfico metade da sua extensão, e seu complemento ocupa a outra metade.
Na figura 135 mostramos o modo como são elaborados os diagramas de Karnaugh para 1, 2 e 3 variáveis, com as expressões lógicas correspondentes a cada caso.
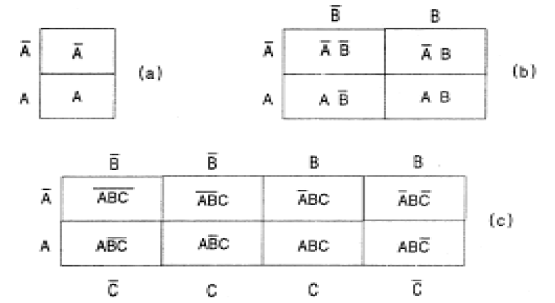
Veja que, para 1 variável, temos 2 casas; para 2 variáveis, 4 casas e para 3 variáveis, 8 casas.
As expressões lógicas, associadas a cada quadrinho, são obtidas de uma forma muito semelhante a usada no conhecido joguinho de "batalha naval" onde a posição de cada "tiro" é dada por duas coordenadas, uma correspondente as linhas e outra às colunas.
Na figura 136 mostramos, como exemplo, de que modo um diagrama de Karnaugh de 4 variáveis pode ser obtido com a inclusão dentro de cada quadro da expressão correspondente.
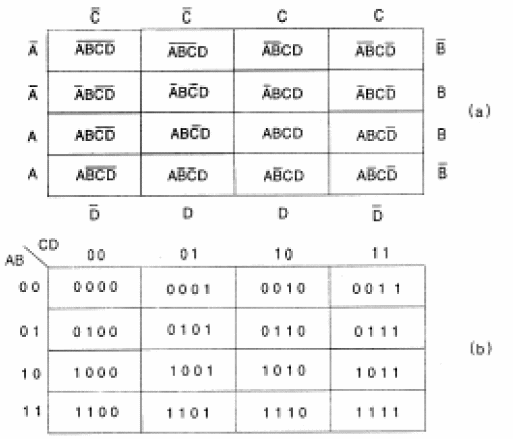
No diagrama (b) da figura 123 os quadros foram preenchidos com os valores 0 e 1 correspondentes às entradas. Este diagrama é chamado também de diagrama de Veitch.
Uma observação importante que pode ser feita em relação a esta representação por 0 e 1, é que cada quadro difere do adjacente em apenas um dígito. Dizemos que são adjacentes os termos que estão à direita e a esquerda de cada quadro e, também, os que estão acima e abaixo. Também são adjacentes os que estiverem na mesma fila, mas um na primeira coluna e outro na última.
Na figura 137 temos um mapa com a identificação das adjacências.
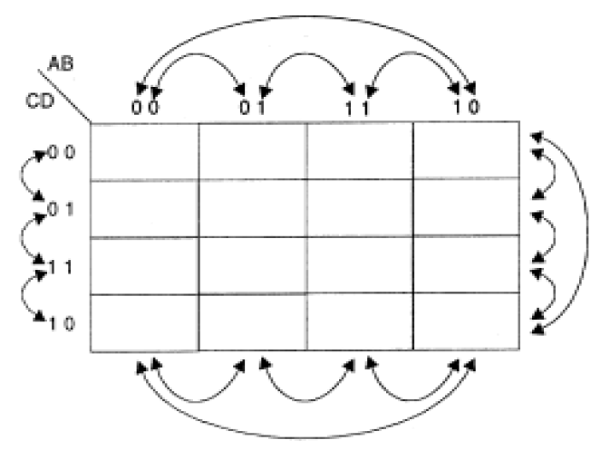
Assim, para podermos fazer as simplificações, o que fazemos é plotar a tabela verdade da função que desejamos implementar num mapa de Karnaugh. Com isso, será possível identificar melhor as adjacências, e assim fazer as simplificações que levam ao uso mínimo de funções lógicas na implementação de um circuito.
Para que o leitor entenda como "funciona" o mapa de Karnaugh numa simplificação de uma função, vamos tomar como exemplo uma função relativamente simples, função que é dada pela seguinte tabela verdade:
| A | B | S |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Desejamos expressar essa tabela como uma soma de produtos, o que significa que os valores adjacentes que devemos procurar na tabela, são os "1". Se fossemos expressar esta função como o produto de uma soma, os valores considerados seriam os "0", e o procedimento final seria o mesmo.
Construímos então o Diagrama de Karnaugh para esta tabela conforme mostra a figura 138.
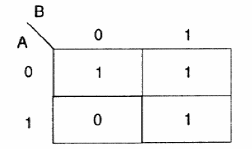
A partir deste diagrama, nosso próximo passo consiste em se tentar fazer simplificações que possam levar a circuitos mais simples na implementação.
A ideia é então agrupar os termos adjacentes, que sejam iguais, havendo para isso diversas possibilidades que são mostradas na figura 139.
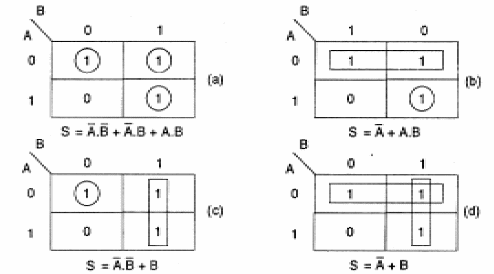
A primeira possibilidade que é mostrada em (a) nos leva a uma soma de três produtos, cada qual obtido pela intersecção da linha com a coluna em que está o "1" correspondente.
Assim, o primeiro está na coluna que intercepta A-0 com B-0. Ora, o valor zero na indexação indica inversão, portanto, isso significa que o primeiro fator de nosso produto será:
/A. /B
O segundo "1" a ser considerado está na coluna A = 1 e B = 0 portanto temos A invertido e B sem inversão, o que nos leva ao segundo fator de nosso produto:
A./B
Finalmente, o terceiro "1" a ser considerado está na linha A = 1 e B = 1 o que significa um fator com A, multiplicado por B sem inversões ou:
A.B
Como devemos expressar a função na forma de uma soma de produtos fazemos:
S = /A./B + A./B + A.B
Para o segundo caso (b), temos uma simplificação maior já que agrupamos os dois "1" da primeira linha de modo que podemos adotar para ele:
/A
Para o outro valor "1" que está na casa que corresponde à intersecção de A =1 com B = 1 vale a soma (sem inversão):
A + B
A expressão final na forma de um produto de somas ser então:
S = /A + B.A
Da mesma forma, chegamos a simplificação (b) que é a que permite a obtenção de uma expressão mais simples, pois conseguimos juntar três casas adjacentes.
Raciocinando da mesma forma chegamos à expressão:
S = /A + B
O procedimento que vimos como exemplo, envolveu uma função simples, com apenas duas variáveis de entrada. No entanto, exatamente o mesmo procedimento é válido para qualquer número de variáveis.
Os leitores interessados num aprofundamento devem procurar treinar os procedimentos indicados trabalhando com funções cada vez mais complexas.
Obras mais avançadas, que tratam de lógica digital, devem ser consultadas para os que desejarem ir além, já que a finalidade desse curso é uma introdução à eletrônica digital.
Outros métodos de simplificação existem como o Método Tabular de Quine-Mac Cluskey que são mais apropriados para a simplificação de equações de mais de 5 variáveis. Esse método é recomendado para número elevado de variáveis, já que o método de Karnaugh torna-se muito complicado para se usar com mais de 5 variáveis.
Conclusão
Não é finalidade deste livro um aprofundamento maior no assunto, e certo treino se faz necessário, para que o leitor domine as técnicas envolvidas.
Assim, para os leitores interessados em se aprofundar no tema, sugerimos a procura de literatura complementar mais completa.
O que mostramos aos leitores é que existem procedimentos lógicos que permitem trabalhar com as funções de modo a se chegar aos circuitos práticos e depois fazer sua implementação.
Assim, a partir de uma tabela verdade que tenha qualquer combinação de entradas que nos leve a qualquer combinação de saída, pode ser elaborada na prática com funções básicas (NOR e NAND) e isso não exige que se "quebre a cabeça".
Conhecendo os procedimentos para se resumir tudo em produto de somas e soma de produtos e também o uso dos mapas de Karnaugh para simplificação pode-se obter configurações simples que facilitam qualquer projeto.
Em suma, a partir de qualquer combinação de entradas e saídas pode-se obter o circuito que as realize a partir de funções lógicas comuns, usando os procedimentos que descrevemos nessa lição.
Também é importante observar que, com poucas funções básicas, podemos ter qualquer combinação possível de comportamentos para o circuito implementado.
Índice
Curso de Eletrônica Digital – Analógica e Digital – Sistemas de Numeração (CUR5001)
Curso de Eletrônica Digital – A Álgebra de Boole (CUR5002)
Curso de Eletrônica Digital – Famílias de Circuitos Lógicos Digitais (CUR5003)
Curso de Eletrônica - Eletrônica Digital – A Família de Circuitos Integrados CMOS (CUR5004)
Curso de Eletrônica Digital – Combinando Funções Lógicas - (Lógica Combinacional) (CUR5005)
Curso de Eletrônica - Eletrônica Digital - Os Elementos Biestáveis (CUR5006)
Curso de Eletrônica - Eletrônica Digital - Flip-Flops e Funções Integradas em CIs (CUR5007)
Curso de Eletrônica - Eletrônica Digital - Os Multivibradores Astáveis e Monoestáveis (CUR5008)
Curso de Eletrônica - Eletrônica Digital - Os Contadores Digitais (CUR5009)
Curso de Eletrônica - Eletrônica Digital - Memórias, ADCs e DACs (CUR5013)


















