Neste artigo, descrevemos os conceitos básicos sobre amostragem analógica, incluindo as definições e cálculos de largura de banda, taxa de amostragem, frequência de Nyquist, aliasing, filtros anti aliasing, erro de quantização e dithering.
Guilherme Kenji Yamamoto, Renan Machado de Azevedo, Renato Araújo de Andrade - National Instruments
Nota: Artigo publicado na revista Saber Eletrônica 474 de novembro/dezembro de 2013.
Largura de banda: definição e cálculos
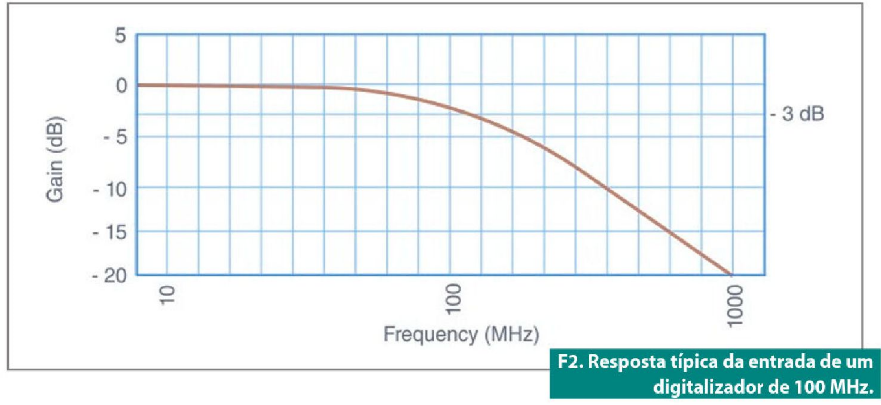
Largura de banda é uma característica de um circuito ou canal de transmissão, definida pela faixa de frequência dentro da qual um sinal é transmitido por este circuito ou canal sem sofrer atenuação significativa. A largura de banda é medida entre os pontos de frequência inferior e superior, nos quais a amplitude do sinal cai 3 dB abaixo da frequência da banda de passagem. Os pontos de -3 dB são chamados de pontos de meia potência.
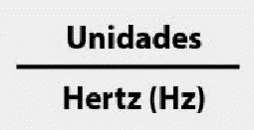
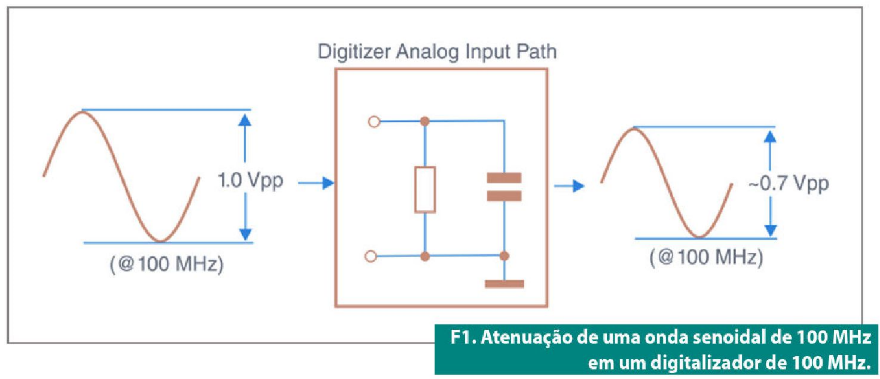
Exemplo: Se você introduzir uma onda senoidal de 100 MHz com amplitude de 1 V em um digitalizador de alta velocidade que tenha uma largura de banda de 100 MHz, o sinal será atenuado pela entrada analógica do digitalizador e a forma de onda amostrada terá uma amplitude de aproximadamente 0,7 V. O valor de aproximadamente 0,7 V pode ser calculado pela fórmula abaixo:

Veja as figuras 1 e 2, a seguir.
Erro de amplitude teórico de um sinal medido
Para que tenhamos o menor erro possível de amplitude no sinal capturado, é recomendado que a largura de banda de seu digitalizador seja de 3 a 5 vezes a componente de maior frequência de interesse no sinal medido (largura de banda necessária = (3 a 5) x a frequência de interesse). O erro de amplitude teórico de um sinal medido pode ser calculado a partir da relação (R) entre a largura de banda do digitalizador (B) e a frequência do sinal de entrada (fin).
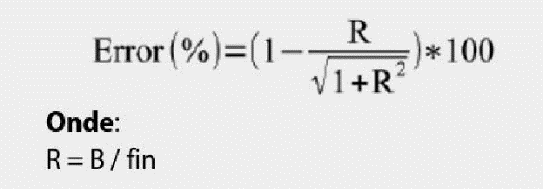
Conforme o cálculo mostrado, o erro em amplitude obtido quando medimos uma onda senoidal de 100 MHz com um digitalizador de alta velocidade de 100 MHz (o que nos dá uma relação R=1) será de aproximadamente 29,3%. No exemplo mostrado na figura 1, isso significa que se a forma de onda de entrada tiver urna amplitude de pico de 1 V, a forma de onda de saída teria uma amplitude pico a pico de aproximadamente 0,707 V. Em outro exemplo, se introduzirmos uma onda senoidal de 75 MHz em um osciloscópio da National Instruments que tenha urna largura de banda de 150 MHz, teremos R=2. Baseando-nos nesse cálculo, teríamos um erro teórico de amplitude de aproximadamente 10,6%.
Tempo de subida
Outro tópico importante relacionado à largura de banda é o tempo de subida. O tempo de subida de um sinal de entrada é o tempo que o sinal leva para passar de 10% a 90% da amplitude máxima do sinal. Esse parâmetro é inversamente proporcional à largura de banda. Observe a figura 3.
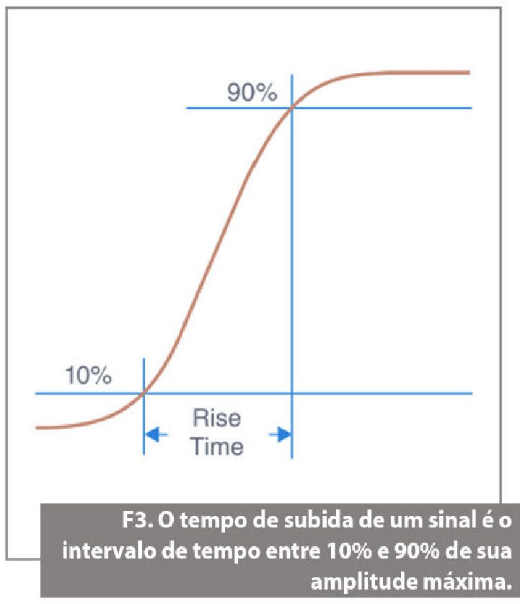
É recomendável que o tempo de subida na entrada do digitalizador seja de 1/3 a 1/5 do tempo de subida do sinal medido, para que possamos capturar o sinal com um mínimo de erro de tempo de subida. O tempo de subida teórico medido (Trm) pode ser calculado a partir do tempo de subida do digitalizador (Trd) e o tempo de subida real do sinal de entrada (Trs).
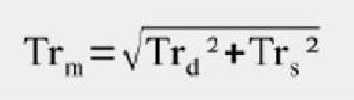
Taxa de amostragem A taxa de amostragem mostra a quantidade de dados coletados em um determinado intervalo de tempo. Ela não está diretamente relacionada à especificação de largura de banda do digitalizador de alta velocidade. A taxa de amostragem é a velocidade na qual o ADC do digitalizador converte o sinal analógico da entrada em valores digitais, Dessa forma, o digitalizador amostra o sinal após as etapas de atenuação, ganho, filtragem e outras similares terem sido aplicadas na entrada analógica, convertendo a forma de onda resultante em uma representação digital. A taxa de amostragem de um digitalizador de alta velocidade é baseada no clock de amostragem que controla os pontos no tempo em que o ADC faz a conversão dos valores analógicos instantâneos em valores digitais.

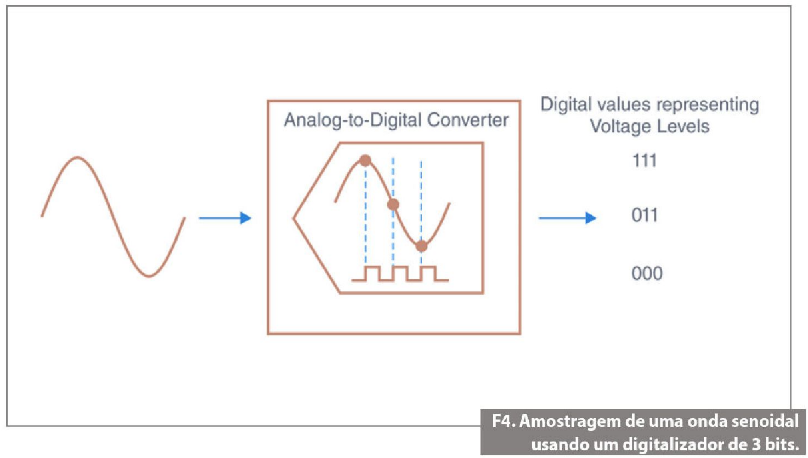
Exemplo: Os digitalizadores de alta velocidade da National Instruments podem oferecer uma taxa variável de amostragem, derivada da taxa máxima de amostragem do dispositivo. A taxa máxima de amostragem do dispositivo é determinada pela taxa de oscilação de seu oscilador a cristal (um componente do hardware do dispositivo). É possível obter, entretanto, taxas de amostragem menores, dividindo a taxa máxima de amostragem por um valor inteiro. Por exemplo, o digitalizador de alta velocidade NI 512 tem uma taxa máxima de amostragem de 200 MS/s. Dessa forma, ele pode ser configurado em taxas de 200/n MS/s, onde n = 1,2,3,4... Atente para a figura 4.
Teorema de Nyquist e frequência de Nyquist
Teorema de Nyquist: Taxa de amostragem (fs) > 2 x componente da maior frequência de interesse do sinal medido. O teorema de Nyquist diz que um sinal deve ser amostrado a uma taxa maior que duas vezes a componente de maior frequência de interesse no sinal para que essa componente seja capturada. Caso isso não ocorra, o conteúdo de alta frequência será representado incorretamente em uma frequência que está dentro do espectro de interesse (banda de passagem). Veja box 1.
Qual é a taxa de amostragem que devo usar?
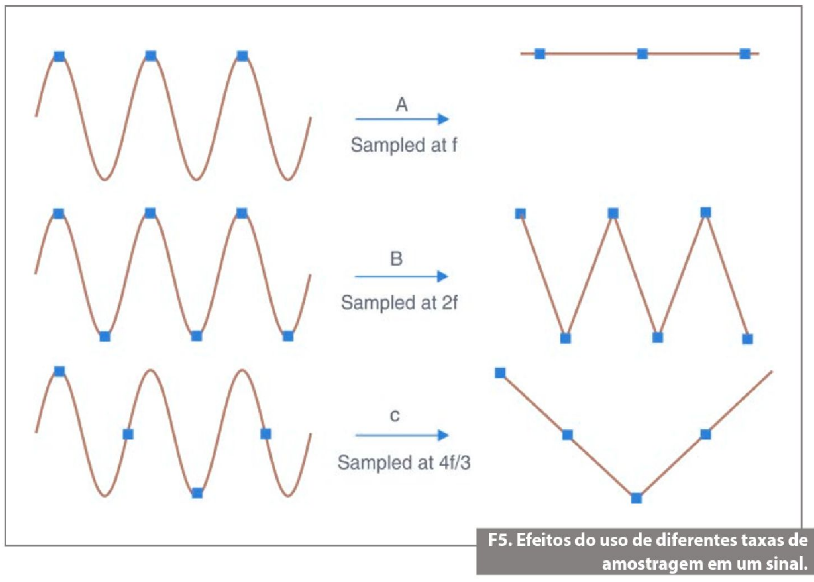
A figura 5 mostra os efeitos das diversas taxas de amostragem. No caso A, a onda senoidal de frequência f é amostrada na mesma frequência f. A forma de onda reconstruída aparece como uma onda "alias” CC, de frequência igual a zero. Entretanto, se você elevar a taxa de amostragem a 2f, a forma de onda digitalizada terá a frequência correta (mesmo número de ciclos), mas será exibida como uma forma de onda triangular. Neste caso (B), f será igual à frequência de Nyquist.
Aumentando a taxa de amostragem a um valor muito acima de f, por exemplo, 5f, você poderá reproduzir a forma de onda com exatidão. No caso C, a taxa de amostragem será 4f/3. A frequência de Nyquist, nesse caso, será (4f/3)/2 = 2f/3. Como f está acima da frequência de Nyquist, essa taxa de amostragem reproduzirá uma forma de onda com aliasing, de frequência e formato incorretos.
Aliasing e filtros anti-aliasing
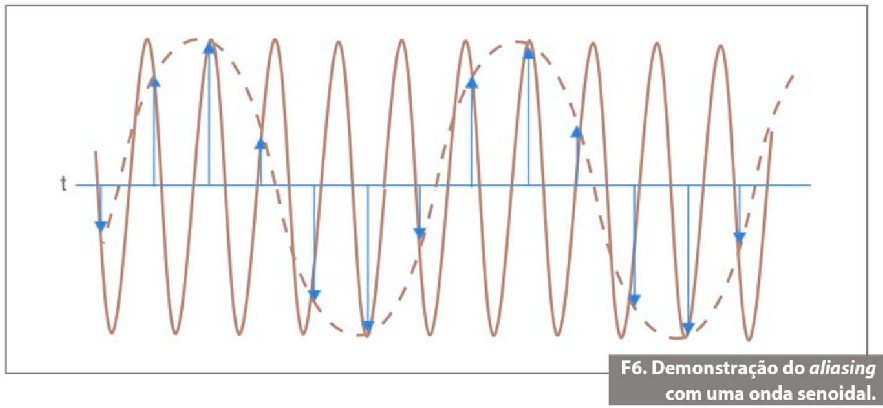
Se um sinal for amostrado em uma taxa de amostragem menor que duas vezes a frequência de Nyquist, uma ou mais componentes de frequência mais baixa aparecerão nos dados amostrados. Esse fenômeno é denominado aliasing. A figura 6 mostra uma onda senoidal de 5 MHz digitalizada por um ADC de 6 MS/s. A linha pontilhada indica o sinal com aliasing registrado pelo ADC. O efeito de aliasing mostra a frequência de 5 MHz incorretamente dentro da banda de passagem, representando-a como se fosse uma onda senoidal de 1 MHz.
Frequência de aliasing
A frequência de aliasing é o valor absoluto da diferença entre a frequência do sinal de entrada e o múltiplo inteiro mais próximo da taxa de amostragem.
Frequência de aliasing = ABS (múltiplo inteiro mais próximo da frequência de amostragem - frequência de entrada), na qual ABS significa valor absoluto. No mundo real, os sinais normalmente contêm componentes de frequência que estão muito acima da frequência de Nyquist. Pelo efeito de aliasing, essas frequências são incorretamente incluídas aos componentes do sinal amostrado corretamente, resultando em uma distorção dos dados amostrados.
Se em um sistema você quiser executar medições de alta exatidão usando dados amostrados, precisará usar uma taxa de amostragem suficientemente alta (de 5 a 10 vezes a componente de maior frequência no sinal) para evitar aliasing, ou introduzir um filtro anti-aliasing (filtro passa-baixas que atenua quaisquer frequências no sinal de entrada que sejam maiores que a frequência de Nyquist) antes do ADC, para restringir a largura de banda do sinal de entrada de forma a atender o critério de amostragem.
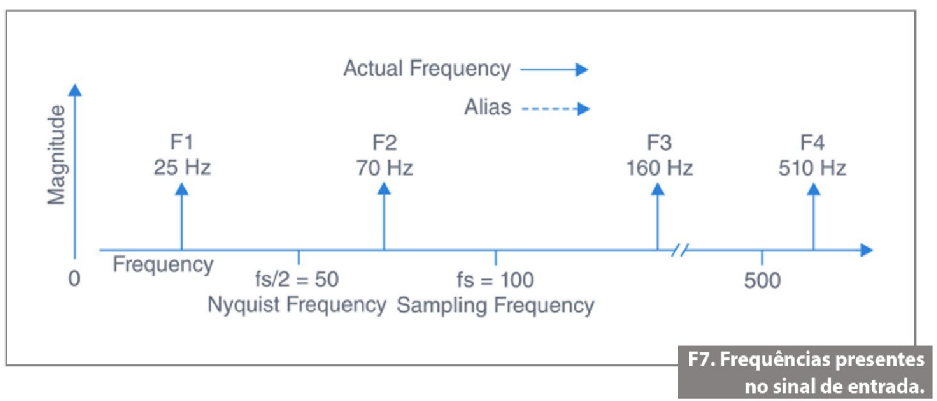
Por exemplo, no dispositivo de aquisição dinâmica de sinais NI 4461 são implementados filtros analógicos e digitais de hardware nas entradas analógicas, para evitar o aliasing. Os sinais de entrada são primeiramente passados por um filtro analógico fixo, para remover quaisquer componentes de frequência que estejam fora da faixa dos ADCs. Em seguida, filtros digitais anti-aliasing ajustam automaticamente suas frequências de corte de forma a remover quaisquer componentes de frequência que estejam acima da metade da taxa de amostragem programada. Exemplo: Assuma que fs, a frequência de amostragem, seja igual a 100 Hz e que o sinal de entrada contenha as seguintes frequências: 25 Hz, 70 Hz, 160 Hz e 510 Hz. Essas frequências são mostradas na figura 7.
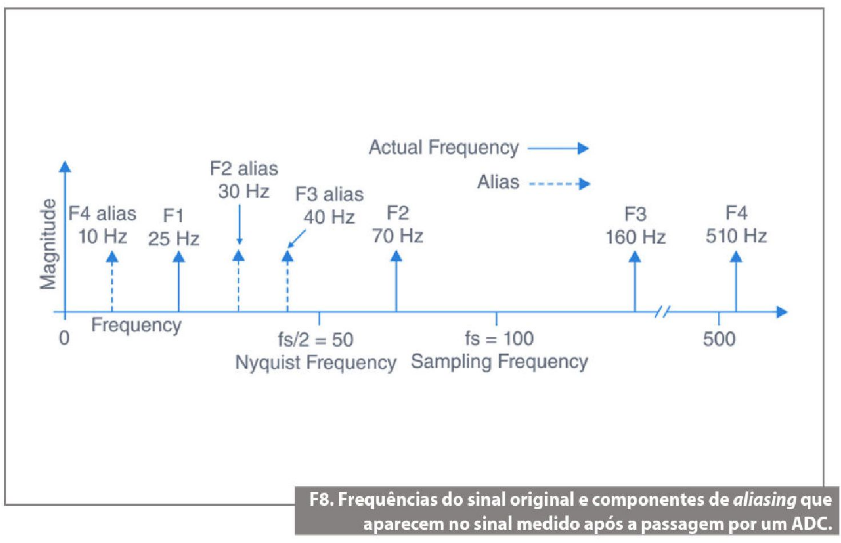
Partindo da figura 8, as frequências abaixo da frequência de Nyquist (fs/2 50 Hz) são amostradas corretamente. Frequências acima da frequência de Nyquist são mostradas como aliases. Por exemplo, Fl (25 Hz) é mostrada na frequência correta, mas F2 (70 Hz), F3 (160 Hz) e F4 (510 Hz) têm aliases em 30 Hz, 40 Hz e 10 Hz, respectivamente. Veja, agora, a tabela 1.
Erro de quantização
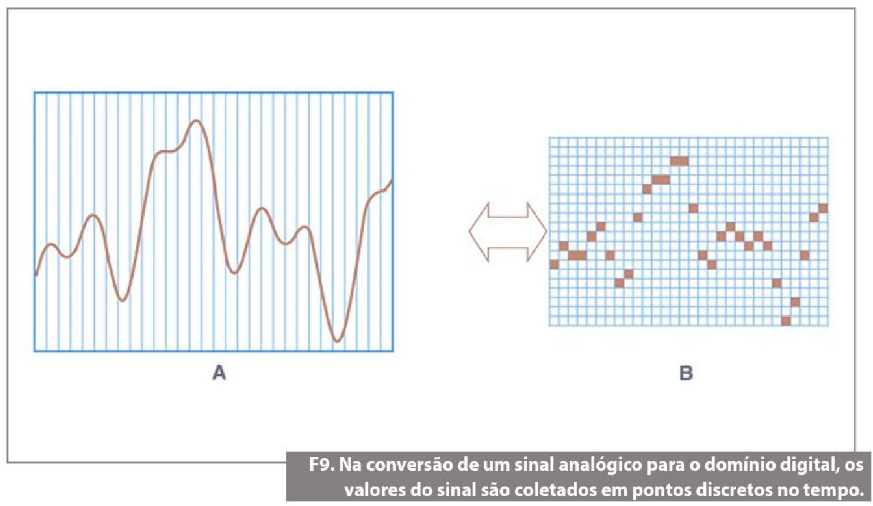
Quantização é o processo pelo qual um sinal analógico é convertido em uma representação digital. A quantização é realizada por um conversor analógico-digital (conversor A/D, ou ADC). Convertendo nossos sinais analógicos em uma sequência de dados digitais, podemos aproveitar a capacidade do computador pessoal e do software para tratar ou aplicar cálculos nos sinais. Para fazer isso, devemos amostrar nossa forma de onda analógica em momentos discretos bem definidos (mas limitados), de forma a mantermos uma relação bem próxima entre o tempo no domínio analógico e o tempo no domínio digital. Se fizermos isso, poderemos reconstruir o sinal no domínio digital, passá-lo por nosso processamento e, posteriormente, reconstruí-lo no domínio analógico, se necessário. Observe na figura 9.
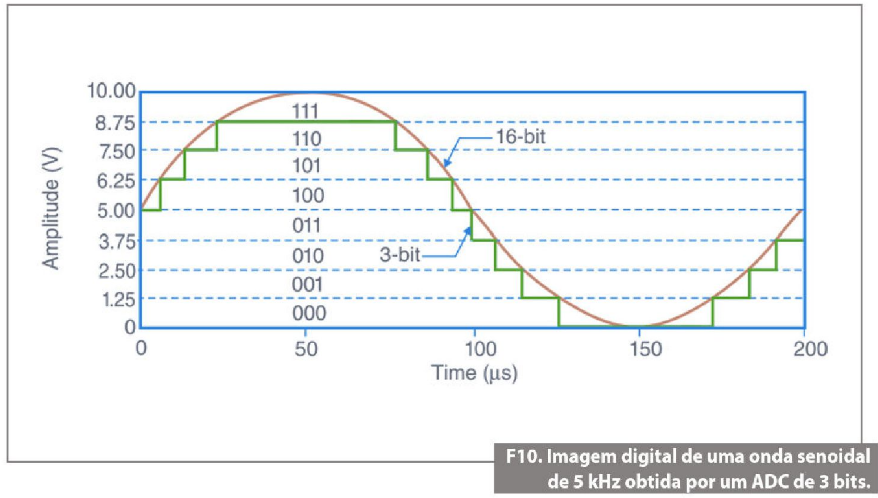
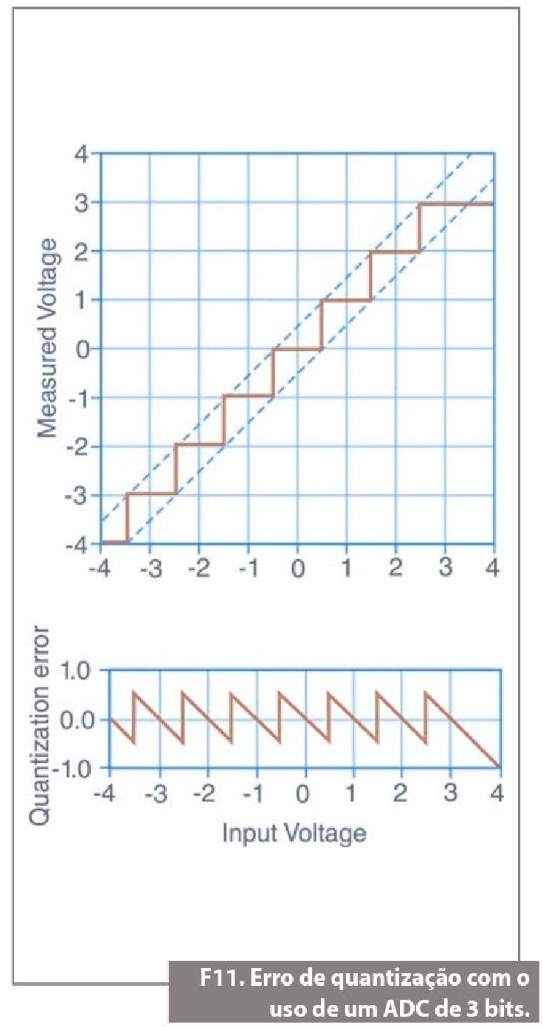
A resolução de tempo que teremos será limitada pela taxa de amostragem máxima do ADC. Mesmo se pudéssemos aumentar nossa taxa de amostragem indefinidamente, ela nunca seria totalmente um "tempo contínuo", como acontece com o sinal de entrada mostrado na figura 9. Mas para a maior parte das aplicações do mundo real, ela ainda será muito útil, apesar de sua natureza limitada. Obviamente, a utilidade de nossa representação digital será maior quanto maiores forem nossa resolução em tempo e amplitude. A resolução em amplitude é limitada pelo número de níveis de saída discretos que tiver o ADC. Por exemplo, um ADC de 3 bits divide a faixa em 23 (ou oito) divisões. Cada uma dessas divisões é representada por um código binário ou digital entre 000 e 111. O ADC traduz cada medição do sinal analógico em uma das divisões digitais. A figura 10 mostra a imagem digital de uma onda senoidal de 5 kHz obtida por um ADC de 3 bits.
Como constatado na figura 11, o sinal digital não representa adequadamente o sinal original, porque o conversor tem uma quantidade pequena demais de divisões digitais para representar as diversas tensões do sinal analógico. Entretanto, aumentando a resolução para 16 bits, para aumentar o número de divisões do ADC de oito (23) para 65.536 (216), teremos, com o ADC de 16 bits, uma representação extremamente exata do sinal analógico. Essa incerteza inerente à digitalização de um valor analógico é denominada erro de quantização. O erro de quantização depende do número de bits no conversor, juntamente com os seus erros, ruído e não linearidades.
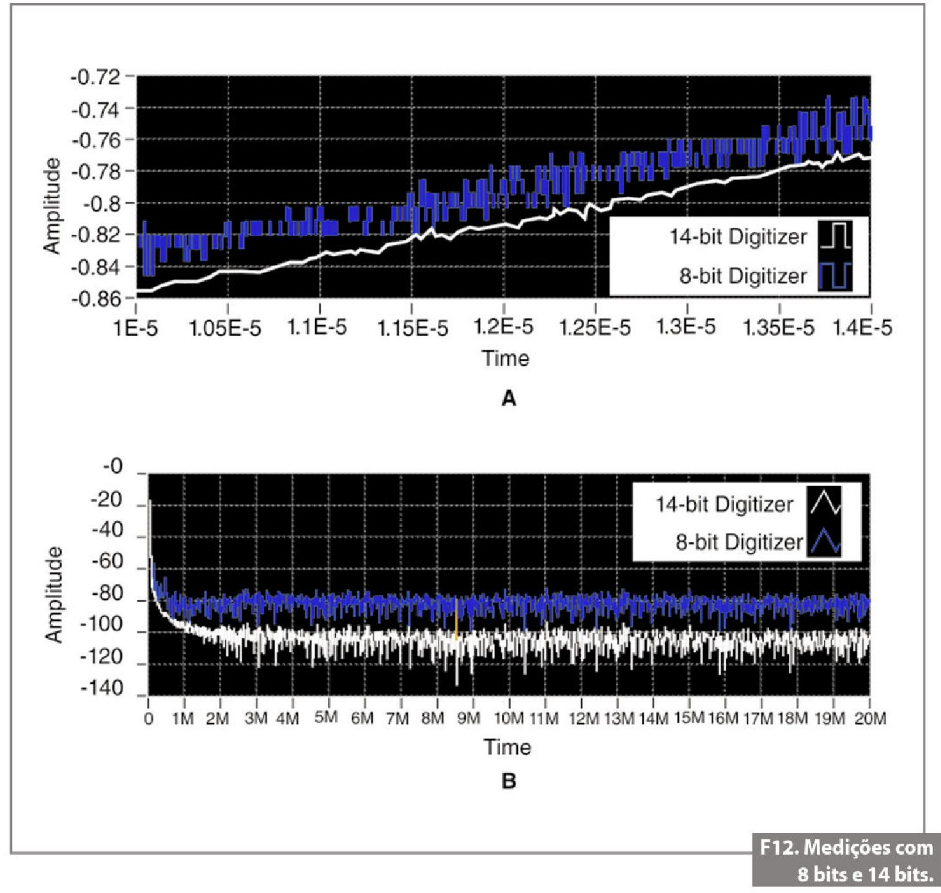
A figura 12 mostra como seria adquirir um sinal na faixa de entrada de 2,5 V usando um digitalizador de alta velocidade NI 5122 de 14 bits e um digitalizador de 8 bits NI 5112. Nesta figura, você pode ver a exatidão na representação de um sinal de entrada obtida com o digitalizador de 14 bits, com 16.384 pontos discretos de tensão, e compará-la com os 256 níveis obtidos com um digitalizador ou osciloscópio de 8 bits. Usando digitalizadores de alta resolução, você poderá também obter vários tipos de medições nos domínios do tempo e da frequência, usando um único instrumento. Esse gráfico mostra claramente as vantagens do uso de um digitalizador de alta resolução nas medições feitas nos domínios do tempo e frequência:
• 8 bits = 256 níveis discretos;
• 12 bits = 4.096 níveis discretos;
• 14 bits = 16.384 níveis discretos.
Dithering
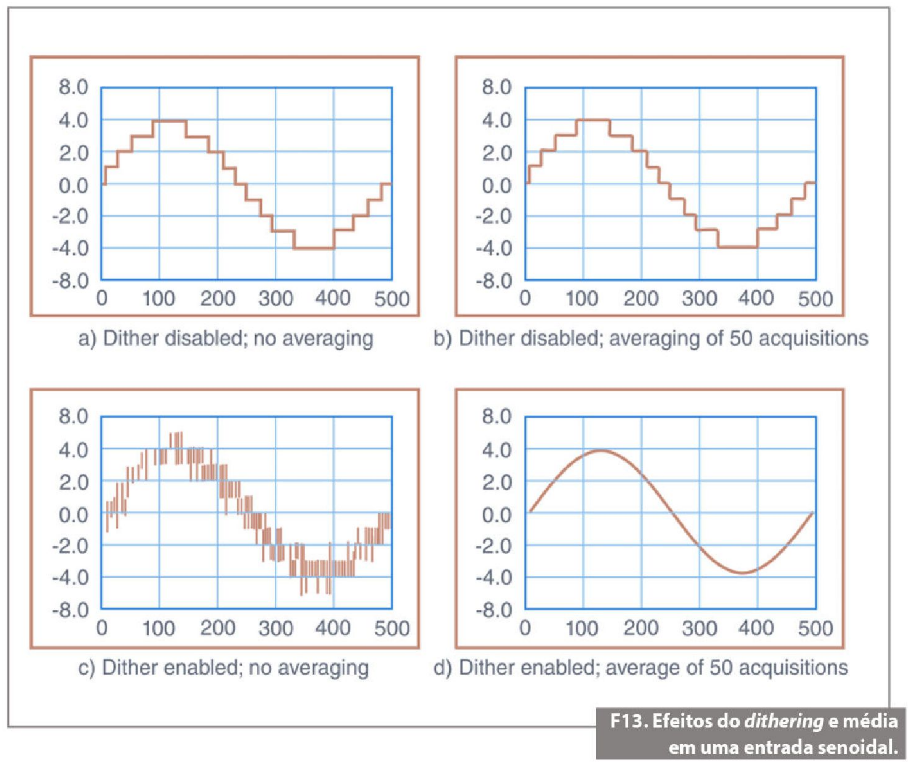
Durante a quantização, no domínio do tempo, podemos preservar quase completamente as informações da forma de onda, fazendo uma amostragem suficientemente rápida. No domínio da amplitude, podemos preservar a maior parte das informações da forma de onda pelo uso da técnica denominada dithering. Dithering é uma inclusão intencional de ruído em nosso sinal de entrada. Essa função atenua pequenas diferenças na resolução de amplitude. O princípio básico dessa função é incluir ruído aleatório de forma a fazer o sinal subir e descer repetidamente entre níveis sucessivos. Obviamente, isso por si só apenas faria o sinal ter mais ruído. Mas esse ruído será suavizado pela função de cálculo do valor médio do sinal no formato digital.
O cálculo matemático do valor médio dos sinais digitais sem o dithering não remove os degraus de quantização. Ele simplesmente os arredonda um pouco, como mostrado na figura 13b.
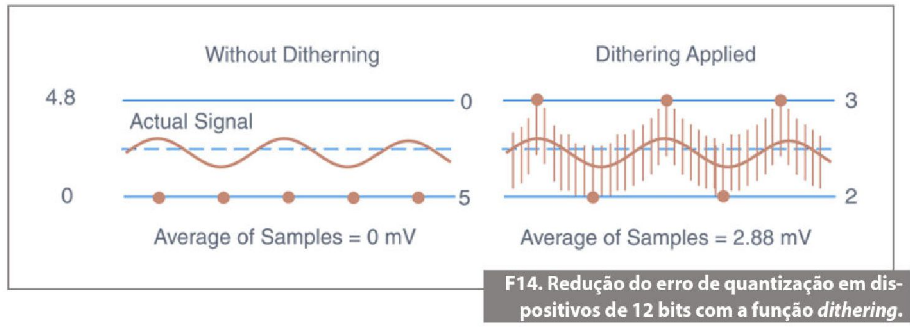
Exemplo: Em alguns produtos de aquisição de dados (DAQ) da série E da National Instruments, como o dispositivo DAQ multifuncional de alta exatidão da série M da National Instruments, o dithering é totalmente habilitado ou desabilitado por software (você não decide como a média é feita no instrumento). Quando habilitado, o software soma aproximadamente 0,5 LSB rms de ruído branco gaussiano no sinal de entrada. Esse ruído é incluído ao sinal antes da entrada no ADC. Como resultado, um sinal que está em algum ponto da menor diferença de tensão detectável pela placa (conhecida como largura de código) agora sobe e desce aleatoriamente até os limites desse código. Quando amostrados, os pontos agora serão exibidos nos limites superior e inferior, e as quantidades de pontos no limite superior ou inferior da largura de código serão proporcionais à localização do sinal. Você poderá então usar a média para aumentar a resolução especificada da placa e obter medições de maior exatidão, menos influenciadas pelo ruído de banda ampla. Por exemplo, quando o dithering estiver habilitado, uma placa de 12 bits poderá trabalhar com resolução de 14 bits. Você pode também desabilitar o dithering em aplicações de alta velocidade, que não utilizam a função de média. Atente para a figura 14.