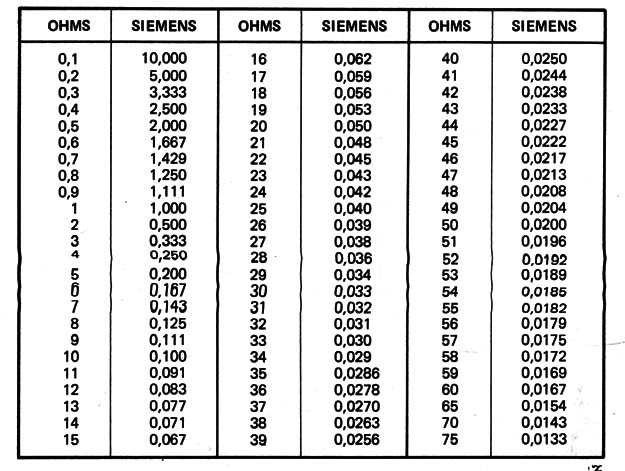
Esta tabela de conversão permite a obtenção das condutâncias associadas às resistências de modo direto podendo ser usada para as mais diversas finalidades.
Podemos definir resistência elétrica como uma oposição à passagem de uma corrente sendo essa grandeza expressa em Ω. Do mesmo modo, podemos falar em condutância como a facilidade que uma. corrente elétrica encontra na sua circulação.
A unidade de condutância é o Siemens.
Assim, podemos estabelecer que a resistência é o inverso da condutância ou em termos matemáticos:
R = 1/G
Onde:
R é a resistência (Ω)
G é a condutância (Siemens).
Muitos cálculos que aparecem projetos eletrônicos exigem a utilização de condutâncias quando o parâmetro conhecido é a resistência e vice-versa o que torna necessário a rápida conversão de uma grandeza em outra.
Se as resistências ou condutâncias trabalhadas forem expressas por números pequenos o seu cálculo é bastante simples, mas se se tratarem de números de dois ou mais algarismos e se o projeto exigir certa precisão, a operação de conversão torna-se trabalhosa principalmente se o leitor não dispuser de uma calculadora ou de uma régua de cálculo.
Evidentemente as coisas se complicam ainda mais se o leitor não for muito seguro na matemática.
Na realidade, em determinados tipos de cálculo, o serviço do projetista fica sensivelmente facilitado se trabalhar em termos de condutância, mesmo que os dados que tenha sejam em termos de resistências.
Um exemplo disso temos no cálculo da resistência equivalente a uma associação de resistores em paralelo.
Na associação em série, conforme o leitor sabe, simplesmente somamos as- resistências associadas, enquanto que numa associação em paralelo, somamos os inversos das resistências associadas para obtermos o inverso da resistência equivalente, ou, em termos matemáticos:
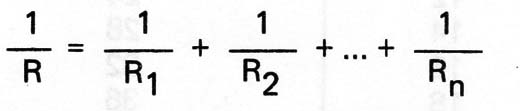
Ora, como o inverso da resistência é a condutância, podemos dizer que obtemos a condutância equivalente a uma associação em paralelo, somando as condutâncias dos resistores associados, ou seja:
G =- G1 + G2 +...+ Gn
O leitor, evidentemente, sabe que somar números inteiros ou decimais é uma operação normalmente mais rápida do que somar números fracionários, principalmente quando os denominadores das frações são diferentes.
Assim, para calcular a resistência equivalente a uma associação em paralelo podemos, pela tabela, encontrar as condutâncias associadas e simplesmente somar seus valores, com o que obteremos a condutância equivalente.
Novamente pela tabela obtemos a resistência equivalente associada.
Lembramos também que a lei de Ohm pode ser expressa em termos de condutância:
G = I/V
Damos a seguir exemplos de aplicação:
1 - Determinar a condutância de um circuito cuja resistência seja de 12 Ω.
Resolução: consultando a tabela, verificamos que na coluna das resistências pó demos encontrar diretamente o valor 12, que corresponde a uma condutância de 0,0833 Siemens.
2 - Determinar a resistência equivalente a associação de um resistor de 20 Ω em paralelo com um resistor de 30 Ω.
Resolução: pela tabela encontramos para as resistências associadas as seguintes condutâncias:
20 Ω .......... 0,05 Siemens
30 Ω .......... 0,033 Siemens
Para obtermos a condutância equivalente, somamos as condutâncias associadas:
G = G1 + G2
G = 0,05 + 0,033
G = 0,083
Novamente, pela tabela, vemos que a condutância de 0,0833 Siemens corresponde a uma resistência de 12 Ω.
Ainda em relação a tabela, vemos que valores de resistências que não se encontram diretamente na tabela podem ter sua condutância determinada facilmente.
Por exemplo: para uma resistência de 200 Ω, que é um valor de resistência 10 vezes maior que 20 Ω, corresponderá uma condutância 10 vezes menor; porque, a condutância é inversamente proporcional à resistência.
Deslocamos assim, a vírgula uma casa para a esquerda:
20 Ω .......... 0,05 Siemens
200 Ω .......... 0,005 Siemens