O que é corrente alternada
Uma corrente que flui sempre no mesmo sentido e com a mesma intensidade, como ocorre quando ligamos uma lâmpada a uma pilha, é chamada "corrente contínua". Podemos abreviar essa designação por CC, ou ainda, usando o termo americano "direct current" por DC. Na figura 172 temos o gráfico que indica a intensidade de uma corrente contínua ao longo do tempo.
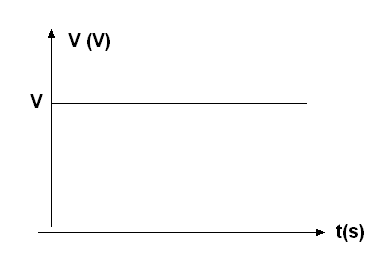
Observe que, para provocar uma corrente contínua precisamos estabelecer em seu circuito uma tensão constante, ou seja, uma tensão que também seja contínua. No entanto, existe outro tipo de corrente que é muito importante, pois é justamente a que dispomos nas nossas tomadas de energia e que as indústrias dispõem para alimentar seus equipamentos: a corrente alternada.
Para entender o que é a corrente alternada vamos partir diretamente do dispositivo ou gerador que a produz, ou seja, o alternador.
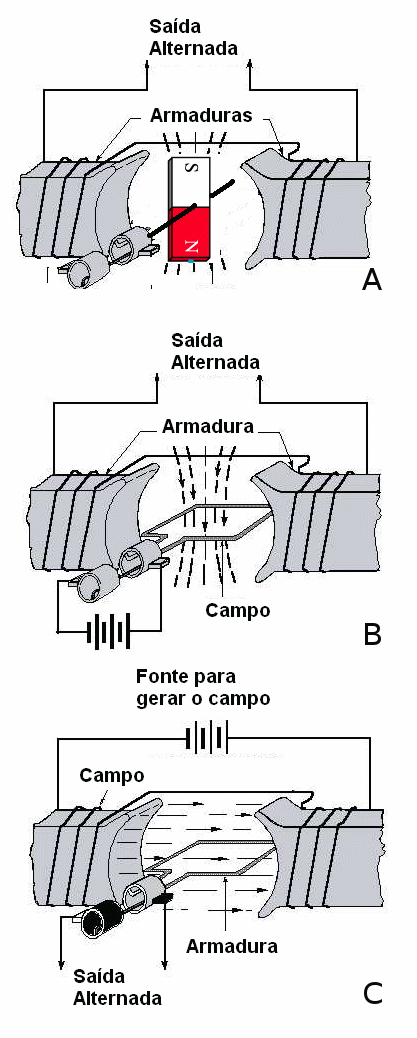
Podemos dizer que existem três tipos diferentes de alternadores mostrados na figura abaixo.
O primeiro (a) tem as armaduras (bobinas) fixas e o campo magnético é produzido por um imã que gira.
O segundo, mostrado em (b) tem a armadura fixa, e o campo magnético é criado por uma segunda bobina que gira.
O terceiro, mostrado em (c) tem uma bobina que cria um campo fixo e uma bobina que gira cortando as linhas de força para gerar a corrente alternada.
Os três tipos são mostrados na figura 173.
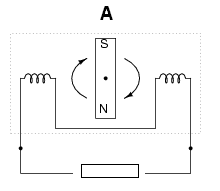
Para entender como funcionam os alternadores, vamos tomar como exemplo o mais simples que é aquele em que um imã permanente gira nas proximidades de duas bobinas.
Nesse dispositivo, um imã parte de uma posição inicial de repouso em que o polo S (sul) está na posição A. Nesse momento ele inicia uma rotação no sentido horário, conforme mostra a figura 174. Não há ainda corrente alguma circulando pela carga.
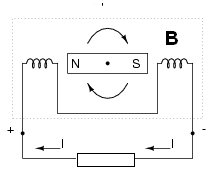
Continuando a girar, vemos que do ponto (A) até o ponto (B), o campo magnético do imã corta as espiras das bobinas criando uma corrente que aumenta de intensidade até atingir o máximo. Essa corrente circula pela carga, conforme mostra a figura 175.
No quarto de volta seguinte, entre ( B ) e (C), o imã continua a cortar as espiras das bobinas, mas de maneira cada vez menos intensa de modo que a corrente na carga se reduz até zero, conforme mostra a figura 176.
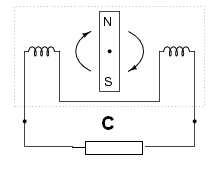
A partir do ponto (C) até o ponto (D) a tensão sobe novamente, mas com polaridade oposta, fazendo agora circular uma corrente em sentido oposto pela carga, conforme mostra a figura 177.
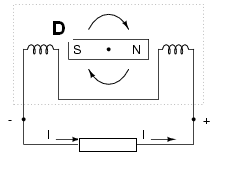
Se o imã continuar girando com certa velocidade, teremos na saída uma corrente que varia entre máximos e mínimos regularmente, ou seja, inverte constantemente de sentido de circulação, o que corresponde a uma corrente alternada.
Vemos então que, se ligarmos um receptor a um gerador desse tipo, metade do tempo de um ciclo, a corrente circula num sentido, e na outra metade ela circula no sentido oposto. A energia que recebemos em nossas casas e que é disponível para consumo geral nas cidades é desse tipo.
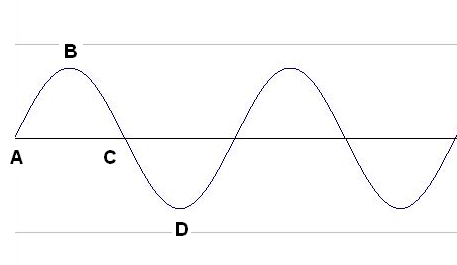
Podemos representar a corrente gerada por esse tipo de gerador por uma curva chamada senóide, conforme mostra a figura 178.
O gerador que produz a energia que consumimos dá 60 voltas por segundo, o que quer dizer que em cada segundo a corrente circula 60 vezes num sentido e 60 vezes no sentido oposto. Dizemos que a corrente que recebemos em nossas casas é alternada com uma frequência de 60 Hertz (Hz).
Existem países, como a Argentina, em que a corrente gerada tem uma frequência diferente, como 50 Hz. O interessante é que os efeitos obtidos na transmissão de energia usando corrente alternada são os mesmos que seriam obtidos com a corrente contínua, com vantagens que ficarão claras no decorrer do curso. Tomemos o seguinte exemplo:
Passando pelo filamento de uma lâmpada ou por um elemento de aquecimento, os efeitos finais são sempre os mesmos: ao serem empurradas, as cargas transferem energia em forma de calor e ao serem puxadas também, o que quer dizer que as lâmpadas acendem do mesmo jeito e os aquecedores aquecem do mesmo jeito.
Formas de onda, frequência, fase e valores
A representação gráfica de uma corrente alternada tem uma forma muito especial: dizemos que se trata de uma forma de onda "senoidal".
Isso nos leva a dizer que a corrente alternada que recebemos em nossas casas e que é distribuída em nossa cidade, é alternada com forma de onda senoidal e frequência de 60 Hz. Analisando essa forma de onda existem diversos valores importantes que o profissional da eletricidade e eletrônica deve conhecer.
O primeiro, de que já falamos, é a frequência que é o número de vezes em cada segundo em que se completa um ciclo da geração dessa energia. A frequência é medida em hertz (Hz). O tempo de duração de um ciclo completo nos dá o período da corrente alternada.
Para uma corrente alternada de 60 Hz, por exemplo, o período ou tempo de um ciclo completo é 1/60 s, conforme mostra a figura 179.
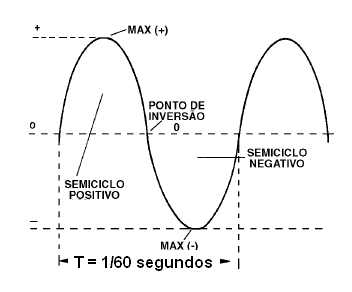
Veja que "o período é o inverso da frequência" ou, escrevendo isso como fórmula:
T = 1/f (f7.1)
Onde:
T é o período (em segundos)
f é a frequência (em hertz)
A amplitude de uma tensão alternada é expressa de diversas formas, conforme podemos observar pela figura 180.
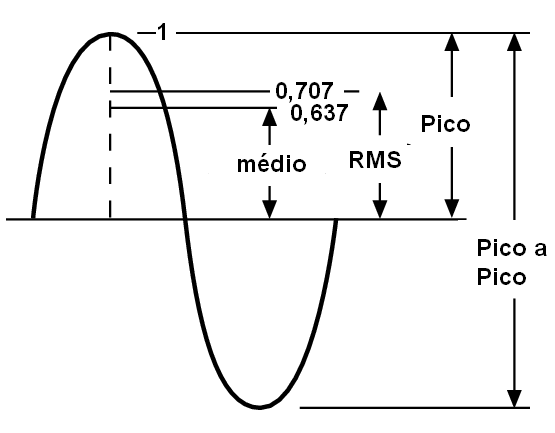
O valor máximo que uma tensão alternada atinge é o valor de pico. Indicamos esse valor por Vp. Metade do valor máximo nos dá o valor médio ou Vm.
No entanto, um valor muito importante é o "valor médio quadrático" ou "root mean square", do inglês, que nos leva a abreviação Vrms. Esse valor corresponde à raiz quadrada de 2 dividida por 2 vezes do valor máximo, ou conforme mostra a fórmula:
Vrms = 0,707 x Vp (f7.2)
Onde:
Vrms é a tensão média quadrática (em volts)
Vp é a tensão de pico
0,707 é a raiz quadrada de 2 (1,41) dividido por 2
Levando em conta que a raiz quadrada de 2 é aproximadamente 1,41, dividindo esse valor por 2, obtemos 0,707. Isso significa que obtemos a tensão rms multiplicando a tensão de pico por 0,707. Da mesma forma, conhecendo a tensão rms obtemos o valor de pico, multiplicando-o por 1,41.
A tensão de "110 V" que encontramos na nossa rede de energia tem esse valor rms. Assim, no instante em que ela se encontra no seu máximo, o pico vai a:
Vp = 1,41 x 110 = 155,1 V
O mesmo é válido para as intensidades de corrente: podemos falar em corrente de pico (Ip), corrente média (Im) e corrente rms (Irms) num circuito.
Um outro valor importante que devemos observar na representação de uma tensão ou corrente senoidal é a sua fase. A cada instante, dentro de um ciclo, a tensão alternada tem um certo valor. Este valor muda constantemente dependendo da frequência da tensão alternada.
Em certas aplicações é importante saber o valor que a tensão ou a corrente num circuito de corrente alternada assume num certo instante dentro do ciclo. Para esta finalidade o que se faz é dividir o ciclo em 360 graus (como numa circunferência) e indicar o instante por um ângulo entre 0 e 360, conforme o leitor poderá constatar pela figura 181.
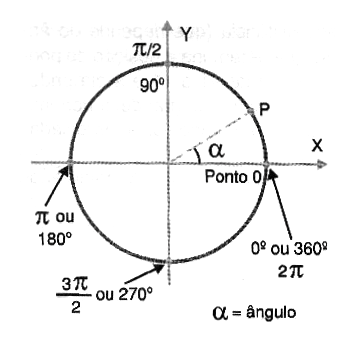
Os 360 graus são adotados lembrando que um ciclo de uma corrente alternada é gerado numa volta completa do alternador. Dessa forma pode-se indicar o instante desejado num ciclo por um ângulo de fase, dado em graus.
Podemos também usar o mesmo conceito para comparar duas correntes ou tensões alternadas que não estejam perfeitamente sincronizadas, ou seja, que não atingem os pontos de máximo e mínimo no mesmo instante. Dizemos que estas correntes estão "defasadas" e podemos indicar a diferença de fase entre elas por um ângulo, conforme pode ser observando se na figura 182.
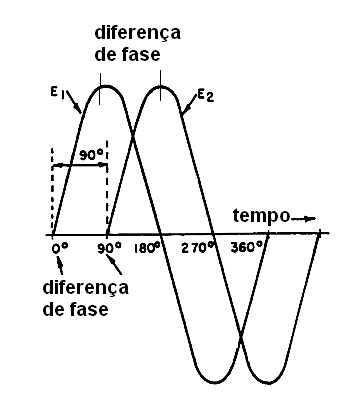
Sinal
Energia pode ser transportada de um lugar a outro, através de fios ou outros meios, utilizando-se uma corrente alternada. No entanto, as correntes alternadas também podem ser usadas para transportar informações. É o que ocorre com circuitos de rádio onde conseguimos alterar as características de uma corrente alternada de frequência muito alta de modo que ela leve informações como voz, imagem, dados, etc.
Quando a corrente alternada é usada para transportar informações, dizemos que se trata de um "sinal".
No caso da rede de energia, as correntes são de baixa frequência, assim como no caso de correntes que correspondem aos sons, cujas frequências variam de 20 Hz a 20 000 Hz (20 kHz). No entanto, correntes de altas frequências, denominadas RF (rádio frequências), podem chegar a bilhões de hertz (GHz).
Alternadores
Os alternadores são geradores que convertem energia mecânica em energia elétrica. No caso específico desses geradores, a energia se torna disponível na forma de correntes alternadas. Encontramos os alternadores em diversas aplicações como, por exemplo, nas usinas hidroelétricas e nos automóveis.
Nas usinas são produzidas grandes quantidades de energia a partir da força das águas represadas ou mesmo do vapor (usinas termoelétricas), enquanto que no automóvel, aproveita-se a força do motor, conforme poderemos ver na figura 183. Uma correia transmite a força do motor para um alternador.
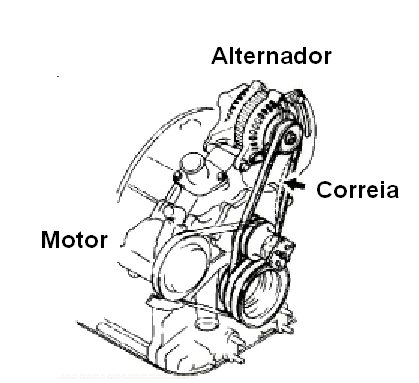
Tanto nas usinas como nos alternadores dos automóveis temos basicamente dois conjuntos de bobinas. Um conjunto rotor que gira para cortar as linhas de força do campo magnético e um conjunto estator que cria o campo magnético, mas não se movimenta.
Energia bifásica e trifásica
A energia que recebemos em nossa casa vem na forma de uma tensão alternada bifásica. Nessa modalidade existe um transformador (cujo princípio de funcionamento será estudado posteriormente) em que se dispõe de duas tensões. Na figura 184 mostramos o que explicamos.
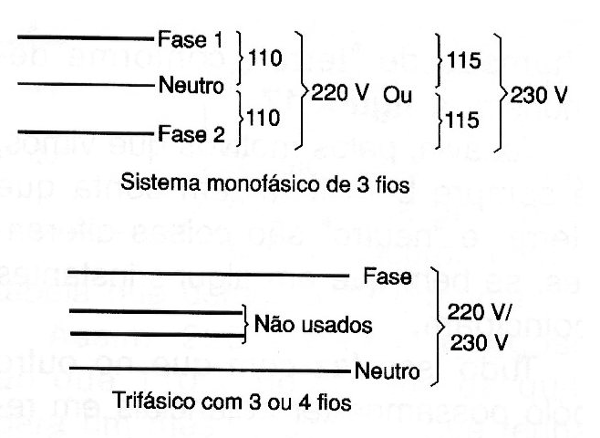
O terminal central é a referência ou polo neutro. Num dos terminais temos uma tensão alternada normal, enquanto que no outro temos uma tensão alternada com a fase invertida, conforme o leitor poderá ver na figura 185.
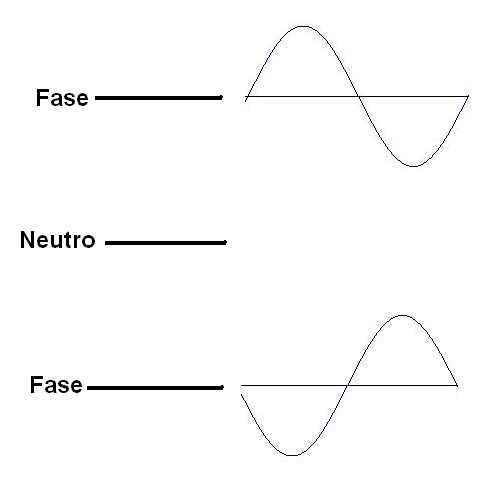
Observe então que as duas tensões têm fases invertidas de tal forma que, quando uma está no pico positivo a outra está no negativo.
Isso significa que, se ligarmos qualquer aparelho entre um dos fios e o neutro ele será alimentado com uma tensão de 110 V. No entanto, se ligarmos alguma coisa entre os fios extremos, a tensão que vai aparecer nele será de 220 V. Essa é a forma de transmissão de energia que muitas empresas usam para fornecer energia doméstica.
O polo neutro normalmente é ligado à terra e assim também é confundido como o "terra" da instalação. Essa ligação tem diversos motivos, dentre eles adicionar segurança e até economizar um dos fios na transmissão da energia.
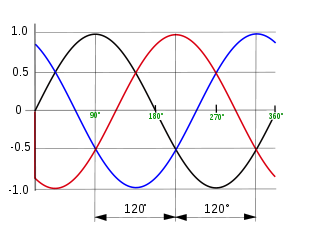
No entanto temos uma outra forma de disponibilizar energia para consumo que é a chamada trifásica. Essa forma de se gerar e distribuir energia em sistemas de corrente alternada é empregada principalmente na indústria, por motivos diversos como, por exemplo, a maior conveniência na alimentação de motores elétricos de alta potência. Veja a figura 186.
Nesses sistemas são geradas três tensões com diferenças de fase de 120 graus, conforme mostra a figura 186.
O que se faz para isso é utilizar um sistema gerador em que temos três tensões alternadas disponíveis em bobinas diferentes, conforme mostra a figura 187. Clique para ver.
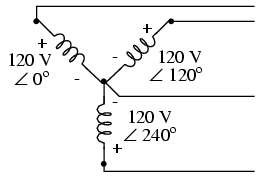
Cada uma das bobinas, que tem uma extremidade ligada a um polo neutro comum, entrega uma tensão senoidal levemente defasada em relação à outra.
Capacitores e Indutores em Corrente alternada
Conforme estudamos nas lições anteriores, quando ligamos capacitores e indutores num circuito de corrente contínua, por exemplo, através de um resistor, eles se comportam de uma maneira bem definida. Os capacitores se carregam até atingir uma carga máxima e os indutores têm sua corrente estabilizada depois de um certo tempo.
O fenômeno que ocorre com esses componentes nos circuitos de corrente contínua ficou bem caracterizado quando falamos de sua "constante de tempo". No entanto, podemos também usar capacitores e indutores em circuitos de corrente alternada.
Quando isso for feito veremos que esses componentes vão se comportar de uma forma completamente diferente que merece um estudo detalhado e muito cuidadoso.
Conforme já estudamos, numa corrente alternada o fluxo de cargas inverte-se rapidamente e de forma constante, no nosso caso à razão de 60 vezes por segundo. Isso significa que em cada segundo a corrente circula 60 vezes num sentido e 60 vezes noutro.
A inversão não se faz de maneira rápida, mas sim suave, de modo que, partindo de um instante em que a corrente é nula, ela cresce suavemente até atingir o máximo num sentido, para depois diminuir até se tornar nula novamente. Depois, ela inverte crescendo suavemente até o máximo no sentido oposto para depois diminuir, isso num processo contínuo que nos dá um gráfico conforme mostra a figura 188.
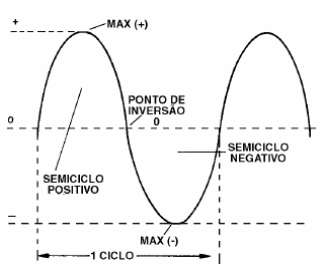
Estudamos que a curva representada neste gráfico recebe o nome de senóide, de modo que a corrente que obtemos nas tomadas de nossa casa é senoidal de 60 hertz. (Alguns países usam correntes de 50 hertz).
Vamos analisar o que acontece se ligarmos um capacitor a um circuito que forneça uma corrente desta conforme o leitor poderá ver na figura 189.
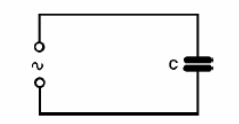
Partindo de um instante em que a tensão seja nula, à medida que ela aumenta de valor numa certa polaridade, ela “bombeia” cargas para o capacitor, que começa a se carregar com a mesma polaridade.
Quando a tensão alternada atinge o máximo num sentido, o capacitor também atinge sua carga máxima. Depois, quando a tensão diminui, as cargas se escoam do capacitor até que, quando a tensão na rede atinge zero, o capacitor também estará descarregado.
No semiciclo (metade do ciclo) seguinte, a corrente começa a aumentar, mas no sentido oposto, carregando assim as armaduras do capacitor com a polaridade oposta, tudo conforme o leitor poderá ver na sequência da figura 190.
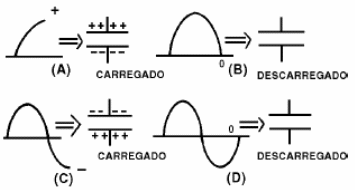
A carga e descarga acompanhando o ritmo de inversão de polaridade da rede, ocorre indefinidamente. Veja que a corrente num capacitor se atrasa em relação à tensão em 90 graus, o que quer dizer que, ela só atinge seu máximo 1/4 de ciclo depois, conforme mostra a figura 191.
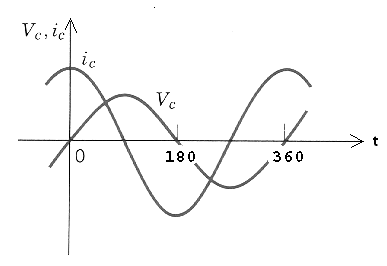
Isso significa que num capacitor, num circuito de corrente alternada, a tensão e a corrente estão defasadas de 90 graus. Dizemos que a corrente, num capacitor num circuito de corrente alternada, está adiantada em relação à tensão em 90 graus.
Veja também que, pela mesma figura 190 que em metade de um semiciclo ele armazena energia com uma polaridade e na outra metade ele a devolve ao circuito.
A quantidade de cargas que é “bombeada” e “extraída” do capacitor depende não só da tensão aplicada, mas também do próprio tamanho do capacitor, ou seja, de sua capacitância. Esta capacitância determina então a corrente média que circula por este componente no processo de carga e descarga, já que não podemos falar num valor em cada instante, pois, conforme vimos, ela varia. Podemos dizer que o capacitor se comporta como uma “resistência” neste circuito, permitindo que uma corrente variável circule.
Como o termo “resistência” não se aplica neste caso, pois o que temos é corrente de carga e descarga circulando, adota-se um outro termo para indicar o comportamento do capacitor no circuito de corrente alternada. Este termo adotado é “reatância” e no caso do capacitor temos uma “reatância capacitiva”, representada por Xc.
O valor de Xc é dado em ohms e depende basicamente de dois fatores: a frequência da corrente alternada e o valor do capacitor. Para calcular a reatância capacitiva apresentada por um capacitor utilizamos a seguinte fórmula:
Xc = [ 1 / (2 x π f x c) ] (f7.1)
Onde:
Xc é a reatância capacitiva (em ohms)
π = 3,14
f é a frequência (em hertz)
C é a capacitância (em farads)
Esta fórmula nos mostra claramente que, à medida que a frequência aumenta temos uma reatância menor, ou seja, a corrente que flui na carga e descarga de um capacitor aumenta.
Simplificando podemos dizer, quando tivermos um capacitor num circuito de corrente alternada ele oferecerá uma oposição menor à passagem das correntes de frequências mais altas, ou seja, aquelas que variarem mais rapidamente. Este comportamento dos capacitores é muito importante quando fazemos o projeto de filtros, ou seja, circuitos que sejam capazes de separar sinais de frequências diferentes.
Impedância
Nos circuitos de corrente alternada em que existem capacitores e indutores não tem sentido falarmos em resistência. Conforme vimos a oposição à passagem da corrente nos circuitos com indutores e capacitores depende de sua reatância a qual é função da frequência.
Assim, para os circuitos de corrente alternada que contém estes componentes o correto é usarmos um termo diferente para a "oposição à passagem da corrente". Este termo é a impedância que também medida em ohm (ohms).
Como um circuito que contém capacitores e indutores também afeta a fase da corrente circulante em relação à tensão, o cálculo de impedâncias envolve valores e também ângulos, ou seja, é feito de uma forma que denominamos "vetorial".
Reatância Indutiva
Do mesmo modo que os capacitores se comportam de formas diferentes nos circuitos de corrente contínua e alternada, os indutores também possuem suas características alteradas. Vamos imaginar um indutor ligado num circuito de corrente alternada, conforme mostra a figura 192.
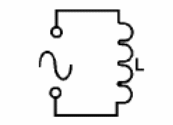
Partindo do instante em que a tensão seja nula no início do ciclo e que também não há corrente circulando, não temos campo magnético na bobina. À medida que a tensão sobe de valor no primeiro semiciclo, a corrente tende a circular num sentido pelo indutor, criando assim um campo magnético que reage ao estabelecimento da corrente. Desta forma, o crescimento da corrente no circuito acompanhando o crescimento da tensão sofre uma oposição.
Quando a tensão atinge seu valor máximo, o campo está totalmente estabelecido, mas ao cair de valor as linhas de força do campo magnético começam a se contrair induzindo uma corrente que tende a se opor a esta nova variação de corrente. No semiciclo seguinte, partindo de zero, a corrente tende a se estabelecer no sentido oposto e o mesmo comportamento do indutor se manifesta tendendo a se opor a estas variações de corrente.
Resumindo, o indutor também tende a apresentar uma oposição ao estabelecimento da corrente alternada a qual depende tanto do valor da indutância como da frequência. Esta oposição que não pode ser chamada também de “resistência”, pois temos um circuito de corrente alternada recebe o nome de reatância indutiva, sendo representada por XL. O valor XL depende tanto da indutância como da frequência podendo ser calculado pela seguinte fórmula:
XL = 2 x π x f x L (f7.2)
Onde:
XL é a reatância indutiva (em ohms)
π vale 3,14
f é a frequência (em hertz)
L é a indutância (em henry)
Observe que a fórmula nos mostra claramente que quanto maior for a frequência da corrente, maior será a oposição encontrada para ela se estabelecer num circuito que exista um indutor. Dizemos que os indutores oferecem uma oposição maior aos sinais de frequências mais altas.
Seu uso em combinação com os capacitores nos circuitos de filtros permite a separação de sinais de frequências diferentes, conforme veremos oportunamente. Na figura 193 mostramos como a corrente e a tensão num indutor estão defasadas de 90 graus.
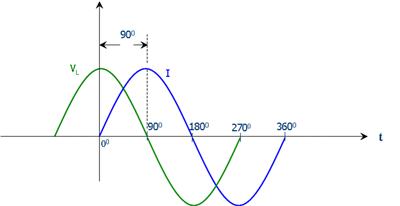
Veja que, da mesma forma que um capacitor perfeito, um indutor não consome energia. Ele simplesmente a absorve, armazenando-a no campo magnético para depois devolvê-la. Nesse processo de absorver e entregar a energia, o indutor se comporta como se apresentasse uma certa oposição à passagem da corrente alternada.
Fator de Potência
Quando um circuito possui indutores, capacitores e resistores combinados, a presença desses componentes pode fazer com que os efeitos do capacitor predominem sobre os efeitos do indutor ou vice-versa. A reatância capacitiva pode ser maior que a indutiva e vice-versa.
Isso nos permite falar em um circuito indutivo ou capacitivo, conforme a corrente e a tensão estejam defasadas segundo uma das formas indicadas. Esta defasagem tem um efeito importante na potência consumida por um aparelho, principalmente os motores de uso industrial.
Fala-se então em "fator de potência" como a diferença de fase entre tensão e corrente que um motor ou outro tipo de carga apresenta quando em funcionamento, mas medida em valores de 0 a 1.
Se a corrente estiver defasada da tensão, como a potência e, portanto, a energia consumida dependem destas duas grandezas, uma falsa indicação pode ser dada. Se este fator for muito pequeno, o consumo do motor será registrado de forma indevida causando problemas para a empresa que fornece energia.
Assim, quando temos uma carga fortemente indutiva que tem um fator de potência baixo, capacitores podem ser associados para fazer a "compensação" corrigindo este fator de modo que ele fique dentro dos limites tolerados, normalmente próximos de 1.
Potência Ativa e Potência reativa
Potência ativa é a que efetivamente realiza um trabalho sendo convertida totalmente em luz, calor, movimento, etc. Essa potência é medida em W (watt) e seus múltiplos (kW ou MW).
Um exemplo de carga que consome totalmente a potência que lhe é fornecida é uma lâmpada incandescente. Ela representa uma carga resistiva pura (ôhmica), conforme mostra a figura 194, pois nela corrente e tensão estão em fase.
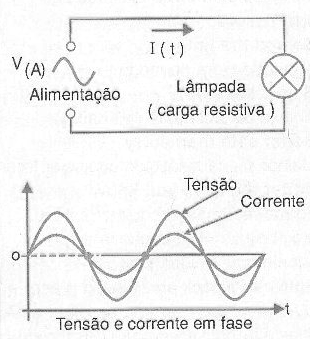
No entanto, em muitas aplicações encontramos cargas que não são resistivas puras, mas sim reativas (capacitores e indutores) como é o caso de motores.
Numa carga deste tipo, a potência é reativa e é medida em VAR (Volt-Ampères Reativos) ou seus múltiplos (kVAR e MVAR), conforme mostra a figura 195.
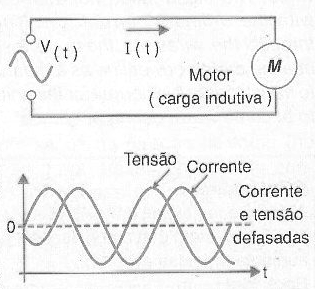
O que ocorre é que nos indutores a potência reativa não é usada na produção de trabalho, pois ela apenas tem por função estabelecer os campos magnéticos. Essa potência, não aproveitada, poderia ser usada com finalidades melhores numa instalação industrial.
A soma vetorial da potência ativa com a potência reativa nos dá a potência real, conforme mostra a figura 196.
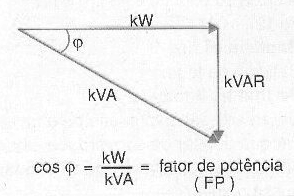
Veja que, se a potência reativa for pequena, o ângulo entre a potência real e a potência ativa diminui, indicando um uso mais eficiente da energia.
Assim, em lugar de se especificar a potência ativa ou a potência reativa, é comum indicar-se a eficiência no fornecimento e uso da energia pelo cosseno do ângulo mostrado na figura 197. Esse ângulo, denominado ? (phi), letra grega que se pronuncia “fi”, tem seu cosseno se aproximando de 1 quando ele tende a zero e ele define o fator de potência.
Desta forma, considerando-se que na figura, esse ângulo pode assumir valores entre 0 e 90 graus, seu cosseno variará entre 0 e 1, conforme mostra a figura 197.
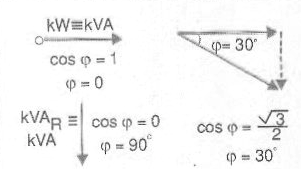
Podemos então dizer que o cosseno de ? pode variar entre 0 e 1. Tanto melhor será o aproveitamento da energia quanto mais próximo o fator de potência (FP) estiver próximo de 1, que é o valor ideal.
Obs. Em inglês usamos o termo Power Factor ou PF.
Também é possível medir o fator de potência como a relação entre a potência ativa e a reativa.
Assim, nas contas de energia temos a especificação dos kVA, mas sim os kVARh (quilowatts-reativos x hora) e os kWh (quilowatts x hora). Para se calcular o fator de potência, deve-se aplicar a seguinte fórmula:
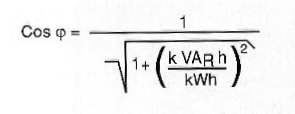
É importante observar que tudo isso é válido quando a energia está dentro dos padrões de qualidade que essas aplicações exigem.
A presença de harmônicas numa instalação altera tudo isso, e a fórmula acima não pode ser aplicada.
Transformadores
Um dispositivo importante que opera baseado no comportamento dos indutores é o transformador. Na figura 198 temos alguns tipos de transformadores, assim como seus símbolos.
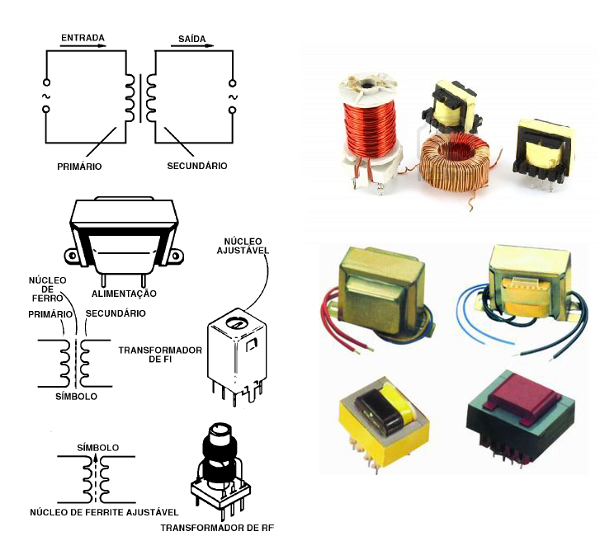
O transformador básico é constituído por duas bobinas enroladas num núcleo comum. O núcleo pode ser feito de diversos materiais como ferrite, ferro laminado, ou mesmo uma forma sem núcleo nenhum, caso em que diremos que se trata de um transformador com núcleo de ar.
Quando estabelecemos uma corrente alternada no enrolamento primário aparece em torno de sua bobina um campo magnético, cujas linhas de força se expandem e contraem na mesma frequência da corrente. O resultado é que, cada vez que estas linhas cortam as espiras do outro enrolamento é induzida uma tensão que aparece nos seus extremos.
A tensão induzida tem polaridade dada pelo movimento das linhas de força, de modo que ela também se inverte na mesma frequência da corrente do primário. Obtemos então no secundário do transformador uma tensão alternada de mesma frequência que a aplicada no enrolamento primário.
Observe então que a energia elétrica passa de um enrolamento para outro, sem contacto elétrico, unicamente através das variações do campo magnético.
Mas, o mais importante de tudo isso é o valor da tensão obtida.
Se o enrolamento primário do transformador tiver 1 000 voltas de fio e o secundário 500 voltas, a tensão obtida no secundário será metade da aplicada, conforme o leitor poderá na figura 199.
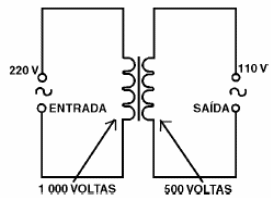
Do mesmo modo, podemos aumentar os valores de tensões alternadas se usarmos transformador cujo secundário tenha mais espiras de fio que o enrolamento primário. Veja, entretanto, que o princípio de conservação da energia se mantém: o que ganhamos em tensão perdemos em corrente, de modo que o produto, que é a potência, se mantém constante.
Assim, se ao aplicar uma tensão de 110 V num transformador, ele “absorve” 1 ampère, ao sair em 220 V, a corrente obtida no máximo só será metade, ou seja, 0,5 ampère. Na prática será um pouco menos, pois os transformadores não têm um rendimento de 100% na transformação de energia, mas sempre um pouco menos.
As "perdas" normalmente vão gerar calor, o que significa que, em funcionamento, os transformadores que trabalham com potências mais elevadas vão se aquecer.
Os grandes transformadores que são usados nas redes de distribuição e mesmo aplicações industriais, trabalhando com potências extremamente altas, podem ter sistemas de refrigeração complexos usando óleo ou mesmo água, com um sistema de circulação forçada.
Os transformadores são usados para abaixar ou elevar tensões nos circuitos ou ainda para “casar” as características dos circuitos, conforme será estudado futuramente. Entretanto, é bom lembrar que para funcionar, o transformador precisa de variações da corrente no seu enrolamento primário. A indução só ocorre quando as linhas de força se expandem ou contraem, ou seja, quando a corrente no primário varia.
Por este motivo, este tipo de componente não pode ser usado em circuitos de corrente contínua pura.
Cálculo de Transformadores
O cálculo completo de um transformador, envolvendo o número de espiras das bobinas, a espessura do fio usado e o tipo de núcleo é algo complexo. O tamanho do núcleo e o material usado, por exemplo, dependem da frequência da corrente e da potência.
Por exemplo, o material usado tem características de saturação que podem influir no modo como o campo magnético tem suas linhas expandidas e contraídas, e isso vai determinar seu rendimento, e a própria produção de calor pelo componente.
A frequência da corrente também é importante pois temos transformadores que não são projetados para operar com a corrente da rede de energia de 60 Hz, mas com correntes de outras frequências. É comum termos transformadores especiais que trabalham com correntes cuja frequência podem atingir várias centenas de quilohertz e até mesmo megahertz.
O cálculo mais simples que podemos fazer é o referente à relação entre o número de espiras e as tensões, conforme a seguinte fórmula:
V1/V2 = n1/n2 (f7.3)
Onde:
V1 é a tensão do primário (em volts)
V2 é a tensão do secundário (em volts)
n1 é o número de espiras do primário
n2 é o número de espiras do secundário
Tipos de Transformador
Na prática encontramos diversos tipos de transformadores nos equipamentos eletrônicos e mesmo em aplicações que envolvam eletricidade. Podemos separar os transformadores em duas categorias:
a) Transformadores para baixas frequências
Os transformadores para baixas frequências são principalmente os que trabalham com sinais da rede de energia de 60 Hz, ou frequências um pouco mais altas em aplicações especiais como amplificadores de som. Esses transformadores usam chapas de metal como núcleo. A finalidade das chapas é diminuir as correntes que são induzidas e que podem provocar o aquecimento do componente.
Na figura 200 temos exemplos de transformadores desse tipo.

b) Transformadores para altas frequências
Os transformadores para altas frequências têm núcleos de materiais especiais como ferrites ou então núcleos de ar. A forma do núcleo também pode variar, existindo alguns tipos que usam anéis (toroides) para essa finalidade. Veja na figura 201 alguns exemplos de transformadores dessa categoria.

Encontramos os transformadores de altas frequências em circuitos de fontes chaveadas, transmissores, receptores de rádio, etc.
O Transformador de Força
Um local em que encontramos um importante transformador para a maioria dos equipamentos eletrônicos é a fonte de alimentação.
Os circuitos eletrônicos de muitos aparelhos trabalham com baixas tensões contínuas, normalmente na faixa de 3 a 40 V e nas tomadas temos 110 V ou 220 V alternados. A finalidade da fonte de alimentação é justamente fazer conversão desta energia e um dos componentes principais envolvidos nesse processo é justamente o transformador.
Este transformador também tem uma função importante: ele isola o circuito do aparelho da rede de energia evitando assim que tomemos choques encostando em qualquer parte. A energia da rede é aplicada num enrolamento e a baixa tensão, de 3 a 40 V, é obtida no outro (não estamos considerando alguns componentes intermediários). Isso significa que os dois enrolamentos estão isolados um do outro.
Lembre-se que a tensão e corrente obtidas no secundário do transformador é alternada assim, para obtermos as tensões e correntes contínuas que os equipamentos de baixa tensão normalmente precisam para funcionar, é preciso empregar componentes adicionais que serão estudados no Curso de Eletrônica Analógica.
Impedância
Quando tratamos de circuitos que usam somente resistências puras, ou seja, componentes que se comportam como resistores, podemos aplicar a Lei de Ohm, sem problemas, para calcular seu comportamento elétrico. No entanto, se tivermos um circuito de corrente alternada, e em lugar de apenas resistores, encontrarmos também indutores e capacitores, a Lei de Ohm, como a conhecemos já não vale.
Se tivermos somente capacitores ou somente indutores, podemos utilizar as fórmulas de reatância capacitiva e indutiva, conforme estudamos, mas tudo isso muda quando combinamos esses componentes, obtendo assim circuitos RLC. Se, por um lado os capacitores têm a corrente adiantando-se em relação à tensão e os indutores atrasando, enquanto os resistores as têm em fase, como combinar tudo isso para obter os efeitos finais no comportamento desse circuito?
O efeito conjunto é denominado "impedância" e se pode dizer que corresponde, de uma forma simplificada" à "resistência" que um circuito apresenta a uma corrente alternada. Evidentemente, a impedância, apesar de medida em ohms não representa apenas uma simples oposição à passagem da corrente, pois ela leva em conta efeitos sobre a fase da corrente em relação à tensão.
Um exemplo de como a impedância pode ser calculada é dado inicialmente combinando-se um resistor e um capacitor, conforme o leitor poderá ver na figura 202.
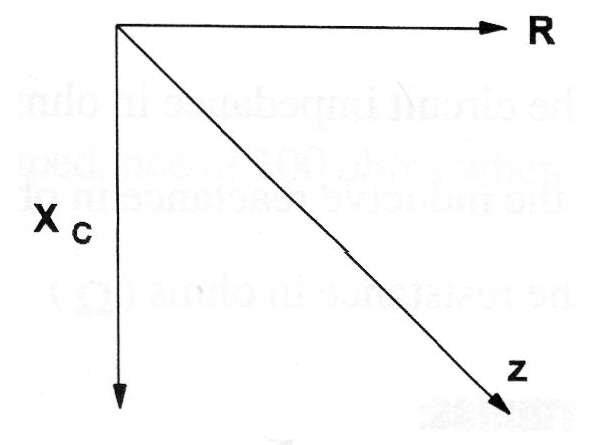
O resistor apresenta uma resistência pura (ôhmica) enquanto que o capacitor tem uma reatância capacitiva. As duas possuem efeitos diferentes no circuito que, colocados num gráfico ficam deslocados de 90 graus um do outro.
Isso significa que o resultado dos efeitos é uma soma vetorial, ou seja, uma soma que leva em conta a direção e o sentido dos efeitos no gráfico. Assim, chamando a impedância de Z, a resistência de R e a reatância capacitiva de C nesse circuito, calculamos Z pela fórmula abaixo:
f7.4
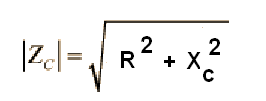
Onde:
Z é a impedância (em ohms)
R é a resistência (em ohms)
Xc é a reatância capacitiva (em ohms)
Podemos também ter o caso de um circuito formado por um indutor e um resistor, conforme mostra a figura 203.
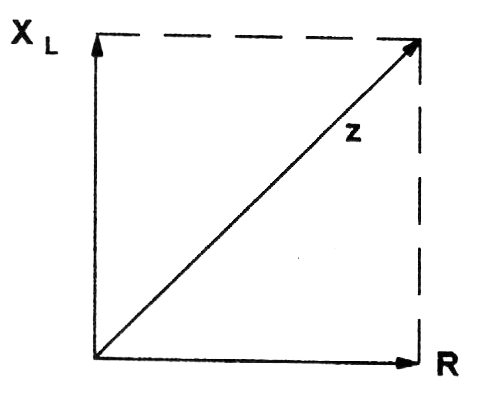
Nesse caso, a reatância indutiva será representada de forma diferente, conforme poderemos ver na mesma figura a resultante que é a impedância.
Chamando de Z a impedância, R a resistência e XL a reatância indutiva, podemos calcular a impedância pela fórmula abaixo:
f7.5
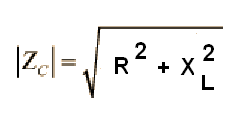
Onde:
Z é a impedância (em ohms)
R é a resistência (em ohms)
XL é a reatância indutiva (em ohms)
Finalmente, temos o caso em que o circuito é formado por um resistor, um indutor e um capacitor como poderá ser visto na figura 204.
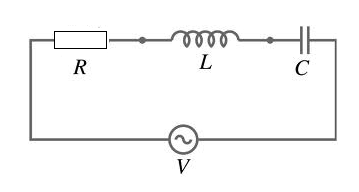
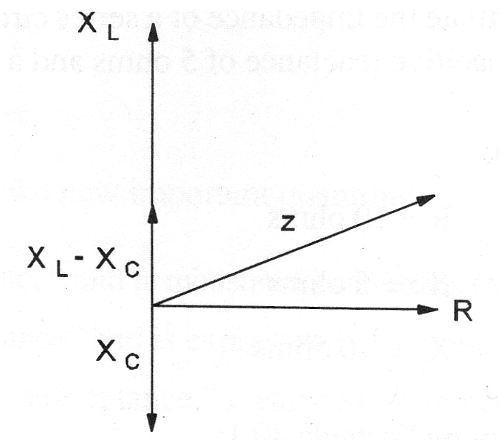
Trata-se de um circuito RLC em que os efeitos das reatâncias e da resistência são colocados na forma gráfica conforme mostra a figura 205.
A impedância desse circuito pode ser calculada pela seguinte fórmula:
f7.6
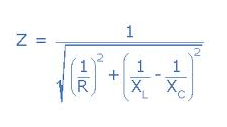
Onde:
Z é a impedância (em ohms)
R é a resistência (em ohms)
Xc é a reatância capacitiva (em ohms)
XL é a reatância indutiva (em ohms)
Observe que a soma da reatância capacitiva com a indutiva é uma soma vetorial, ou seja, devem ser considerados os sinais das grandezas.
As lições deste curso são:
Lição 1 – Matéria e energia, a natureza da eletricidade, eletricidade estática
Lição 2 – Energia elétrica, corrente e tensão. O circuito elétrico
Lição 3 – Resistência elétrica, resistores, Lei de Ohm, Lei de Joule
Lição 4 – Tipos de geradores, rendimento e equação do gerador
Lição 6 – Magnetismo e eletromagnetismo
Lição 7 – Corrente alternada
Lição 9 – Ondas eletromagnéticas



















