Resistividade
Conforme estudamos na primeira lição, não existe um material condutor perfeito. Isso significa que ao forçar a passagem através de qualquer meio, a corrente elétrica encontra uma oposição que denominamos "resistência elétrica". Todos os materiais, por melhores que sejam, sempre representam certo grau de dificuldade para a passagem da corrente, ou seja, para a mobilidade das cargas.
Quanto "de resistência” vai encontrar a corrente para passar através do material dependerá de diversos fatores como, por exemplo, as dimensões do objeto através do qual ela passa,(por exemplo, a espessura e comprimento de um fio) e se o material de que ele é feito é ou não um bom condutor de eletricidade.
A qualidade do material que nos diz se ele é ou não um bom condutor é associada a uma grandeza denominada "resistividade".
Cada material possui, portanto, uma resistividade que é a "quantidade" de resistência que ele pode oferecer a corrente quando o usamos.
Veja, entretanto, a facilidade que a corrente tem para passar pelos materiais não depende apenas de sua natureza, mas também de seu formato. Assim, um fio mais grosso deixa passar com mais facilidade a corrente do que um mais fino.
Isso nos leva a necessidade de enunciar uma segunda grandeza elétrica que é a "resistência". A resistência é o grau de dificuldade que o corpo, dependendo agora do material e da forma, apresenta à passagem de uma corrente.
Assim, devemos falar que a prata tem menor resistividade do que o cobre no sentido de que os fios de prata são melhores condutores de eletricidade. Da mesma forma devemos falar que um fio de 1 metro de comprimento e 1 mm de diâmetro de prata tem menor resistência do que um fio de mesmas dimensões feito de cobre, conforme mostra a figura 47.
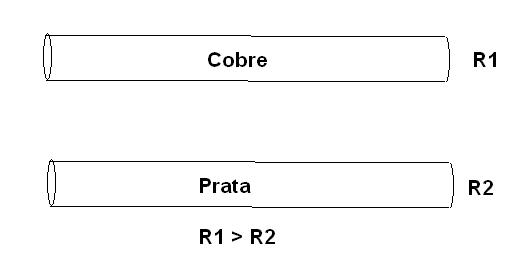
A resistividade é medida em ohm/m.cm2. Damos a seguir uma tabela com a resistividade de alguns materiais comuns:
| Material | Resistividade (Ohm/m.cm2) |
| Alumínio | 0,0292 |
| Antimônio | 0,417 |
| Bismuto | 1,17 |
| Bronze | 0,067 |
| Cádmio | 0,076 |
| Cobre (puro) | 0,0162 |
| Cobre (duro) | 0,0178 |
| Constantan | 0,5 |
| Grafite | 13 |
| Ouro | 0,024 |
| Ferro (puro) | 0,096 |
| Chumbo | 0,22 |
| Mercúrio | 0,96 |
| Níquel | 0,087 |
| Platina | 0,106 |
| Prata | 0,0158 |
| Estanho | 0,115 |
| Tungstênio | 0,055 |
| Zinco | 0,056 |
Nos circuitos elétricos e eletrônicos podemos ter a necessidade de inserir propositalmente uma resistência num ponto, dificultando a passagem da corrente quer seja para limitar sua intensidade, quer seja para obter algum outro tipo de efeito. A redução proposital de correntes e mesmo de tensões num circuito usando componentes que ofereçam uma resistência é algo muito comum nos circuitos eletrônicos de todos os tipos.
Isso nos leva a uma categoria especial de componentes cuja finalidade é apresentar uma resistência elétrica: os resistores.
Resistores
Para reduzir, de maneira controlada, a intensidade da corrente elétrica, oferecendo-lhe uma oposição ou resistência, ou então para fazer cair a tensão num circuito a um valor mais conveniente para uma determinada aplicação, usamos componentes denominados resistores.
Houve tempo em que esses componentes eram chamados “resistências”, confundindo-se com a sua função. Até hoje, alguns profissionais de formação mais antiga e mesmo os que são ligados à área de eletrotécnica chamam os resistores de “resistências”. Os resistores mais comuns são os de película ou filme de carbono ou metálico que têm o aspecto mostrado na figura 48.

Nos diagramas, os resistores são representados por símbolos havendo duas normas básicas, a americana e a europeia, conforme mostra a figura 49.
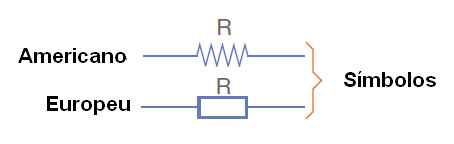
Os resistores possuem três especificações importantes: resistência, tolerância e dissipação. Existem outras especificações que, no entanto, só são levadas em conta em aplicações muito especiais.
A “quantidade” de resistência que um resistor oferece à corrente elétrica, ou seja, sua "resistência" nominal é medida em ohm ( ohms ) podendo variar entre 0,01 ohm e mais de 22 000 000 ohms.
Também usamos nas especificações de resistência os múltiplos do ohm, no caso o quilohm (kohms) e o megohm (Mohms).
Assim, em lugar de falarmos que um resistor tem 4700 ohms é comum dizermos 4,7 k ou simplesmente 4k7, onde o “k” substitui a vírgula (veja nota do autor).
Para um resistor de 2 700 000 ohms falamos simplesmente 2,7 M ou então 2M7.
Como os resistores, em geral, são componentes muito pequenos, os seus valores não são marcados com números e letras, mas sim através de um código especial que todos os praticantes de eletrônica devem conhecer.
Neste código são usadas faixas coloridas conforme explicamos a partir da seguinte tabela:
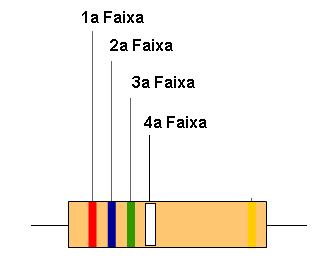
| Cor | Valores Significativos (1a e 2a Faixas) | Multiplicador (3a Faixa) | Tolerância (4a Faixa) | Coeficiente de temperatura (ppm/oC) |
| Preto | 0 | 1 | - | - |
| Marrom | 1 | 10 | 1% | 100 |
| Vermelho | 2 | 100 | 2% | 50 |
| Laranja | 3 | 1 000 | - | 15 |
| Amarelo | 4 | 10 000 | - | 25 |
| Verde | 5 | 100 000 | 0,5% | - |
| Azul | 6 | 1 000 000 | 0,25% | 10 |
| Violeta | 7 | 10 000 000 | 0,1% | 5 |
| Cinza | 8 | 100 000 000 | 0,05% | - |
| Branco | 9 | 1 000 000 000 | - | 1 |
| Dourado | -/td> | 0.1 | 5% | - |
| Prateado | - | 0.01 | 10% | -/td> |
Partindo dessa tabela, podemos determinar não só a resistência de um resistor comum pelas suas faixas, como outras características importantes que serão estudadas nessa lição. A leitura do valor (resistência) é feita considerando-se as faixas coloridas que são lidas da ponta para o centro, conforme mostra a figura 50.
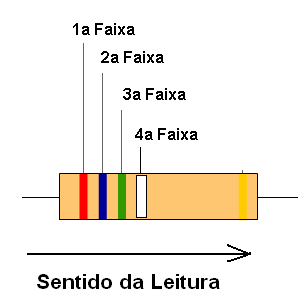
Vamos supor que estejamos de posse de um resistor cujas cores, na ordem de leitura, são: amarelo, violeta, vermelho e dourado (figura 48). Qual será o seu valor (resistência)?
A primeira e a segunda faixa fornecem os dois algarismos da resistência, ou seja:
amarelo = 4
violeta = 7
Formamos assim, a dezena 47.
A terceira faixa nos dá o fator de multiplicação, ou quantos zeros devemos acrescentar ao valor já lido. No caso temos:
vermelho = 00 ou x 100
Temos então 47 com 00 = 4700 ohms ou 4k7.
A quarta faixa nos diz qual é a tolerância no valor do componente, quando ela existe. Se esta faixa não existe, temos um resistor de 20%, ou seja, que pode ter até 20% de diferença entre o valor real da resistência que ele apresenta e o valor que temos na marcação.
Isso significa que na praticam quando compramos um resistor de 1 k x 10% de tolerância, na realidade ele pode apresentar valores entre 900 ohms e 1 100 ohms, sem que isso signifique que ele esteja com problemas.
Veja que essa tolerância é perfeitamente admitida em muitos projetos, onde não é necessário ter uma resistência exata num ponto do circuito. Assim, os resistores (como muitos outros componentes), sempre têm uma certa tolerância.
No nosso caso, a faixa dourada diz que se trata de um resistor com 5% de tolerância.
Todos os profissionais da eletrônica devem memorizar esse código de cores, mesmo porque ele também é usado em outros componentes.
Assim, o marrom = 1 também será usado em outros tipos de componentes para especificar esse valor quer seja na unidade correspondente ou simplesmente para indicar um número de tipo.
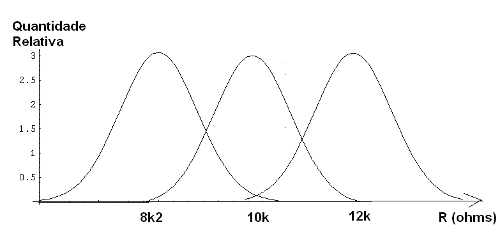
Com isso, um resistor de 10 k cobre a faixa de 9000 ohms a 11000 ohms. Não precisamos fabricar resistores de 9500 ohms, pois usando um de 10 k, com sua tolerância ele funcionará.
Por esse motivo, os resistores (e outros componentes) seguem um padrão de valores que permite cobrir todos os valores possíveis. Assim, com 20% de tolerância precisamos apenas de 6 valores, o que nos leva à série E6 e com 10% precisamos de 12 valores, o que nos leva à série E12 e E24 de 5%, conforme mostra a tabela.
| Valor | E24 | E12 | E6 |
| 1,0 | 5% | 10% | 20% |
| 1,1 | 5% | - | |
| 1,2 | 5% | 10% | - |
| 1,3 | 5% | - | |
| 1,5 | 5% | 10% | 20% |
| 1,6 | 5% | - | |
| 1,8 | 5% | 10% | - |
| 2,0 | 5% | - | |
| 2,2 | 5% | 10% | 20% |
| 2,4 | 5% | - | |
| 2,7 | 5% | 10% | - |
| 3,0 | 5% | - | |
| 3,3 | 5% | 10% | 20% |
| 3,6 | 5% | - | |
| 3,9 | 5% | 10% | - |
| 4,3 | 5% | - | |
| 4,7 | 5% | 10% | 20% |
| 5,1 | 5% | - | |
| 5,6 | 5% | 10% | - |
| 6,2 | 5% | - | |
| 6,8 | 5% | 10% | 20% |
| 7,5 | 5% | - | |
| 8,2 | 5% | 10% | - |
| 9,1 | 5% |
Por exemplo, podemos encontrar um resistor de 8,2 k ohms com 5% ou 10% de tolerância mas não de 20%.Para um resistor de 62 k ohms, só podemos encontrar esse valor com 5% de tolerância.
Existem resistores “de fio” que por serem maiores, têm a marcação de resistência feita diretamente com números e marcações escritas. Na figura 51 temos exemplos de resistores de fio.

Também existem resistores de um tipo denominado SMD (Surface Mounting Device) ou para Montagem em Superfície que são extremamente pequenos e usam um código de diferente. Os resistores SMD são componentes extremamente pequenos, ficando difícil até mesmo a utilização do código de cores na sua marcação.
Na figura em que demos os diversos tipos de resistores, incluímos os do tipo SMD para que o leitor tenha uma ideia de suas dimensões.
Nesse código temos 3 dígitos: os dois primeiros dígitos formam os dois primeiros algarismos da resistência e o terceiro o número de zeros ou fator de multiplicação.
Por exemplo, na figura 52, 103 significa 10 e 000 ou 1 000 ohms.

Vimos nas lições anteriores que quando uma corrente elétrica força a passagem por um meio que lhe ofereça oposição, ela dispende energia na forma de calor. No caso do resistor, se o componente não for capaz de transferir este calor para o meio ambiente, ele acaba por se aquecer demais e queima.
A capacidade que um resistor tem de transferir calor para o meio ambiente está diretamente ligada ao seu tamanho (superfície de contato com o ar). Essa capacidade é dada pela potência (dissipação) do resistor a qual é expressa em watts (W).
Assim, os menores resistores são de 1/8 ou 1/4 W enquanto que os maiores podem chegar a 20 ou mais watts (alguns fabricantes especificam as potências em valores decimais como 0,125 W, 0,25 W, etc.).
Os resistores de grandes potências são de material resistente à altas temperaturas e, em lugar do carbono ou filme metálico, são usados fios de nicromo (uma liga de níquel com cromo). Esses resistores também são chamados resistores de fio.
Fusistores
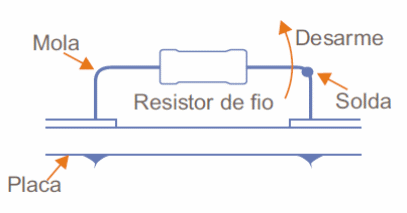
Um tipo de proteção interessante encontrada em alguns aparelhos de consumo, como televisores, consiste na colocação de um resistor de valor baixo (que não altera a corrente no circuito) em série com as principais linhas de alimentação. Quando a corrente excede certo valor, este resistor aquece demais e o calor gerado que se propaga pelo terminal derrete a solda que o prende num sistema de mola, conforme mostra a figura 53. Esse componente é chamado fusistor (de fusível + resistor).
Lei de Ohm
Estudamos na segunda lição de nosso curso que existe uma relação bem definida entre a corrente num resistor e a tensão que a provoca. A intensidade da corrente num determinado meio depende não só da resistência desse meio, mas também da causa dessa corrente, ou seja, da tensão.
Tensão, corrente e resistência são relacionadas de uma forma muito bem definida através da Lei de Ohm.
Essa Lei afirma que a intensidade da corrente num determinado meio que apresente uma resistência é diretamente proporcional à tensão aplicada, conforme sugere a figura 54.
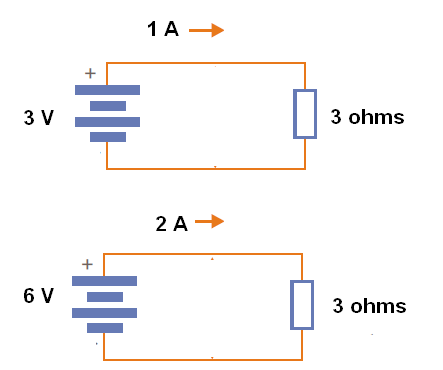
Em outras palavras, a relação entre a tensão e a corrente num determinado meio que apresente certa resistência é uma constante e tem justamente o valor dessa resistência:
Podemos indicar isso através de uma fórmula básica:
R = V/I (f3.1)
Onde:
R é a resistência dada em ohms (Ω)
V é a tensão dada em volts (V)
I é a corrente dada em ampères (A)
Dessa fórmula podemos obter duas outras:
V = R x I (f3.2)
I = V/R (f3.3)
Veja então que usamos a primeira (f3.1) para calcular a resistência quando conhecemos a corrente e a tensão; usamos a segunda (f3.2) para calcular a tensão quando conhecemos a resistência e a corrente e usamos a terceira (f3.3) para calcular a corrente quando conhecemos a tensão e a resistência.
Os dispositivos, tais como os resistores, que seguem a lei de Ohm, ou seja, em que a resistência é uma constante, são denominados dipolos ôhmicos. A palavra dipolo serve para designar componentes ou circuitos que tenham dois polos.
Se colocarmos num gráfico os valores das correntes e tensões correspondentes obtidas num resistor, veremos que a "curva" resultante é uma reta conforme mostra a figura 55.
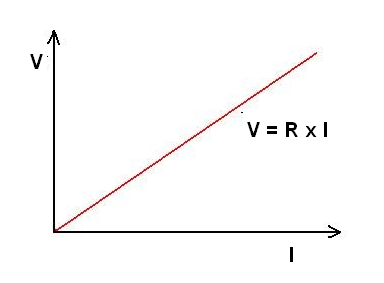
Dizemos então que a "curva" característica de um resistor é linear.
Curva Característica de uma Lâmpada
Conforme estudamos, se num condutor ou outro dispositivo a corrente for diretamente proporcional à tensão aplicada, ou seja, a corrente aumenta na mesma proporção em que aumentamos a tensão temos um dispositivo ou dipolo que segue a Lei de Ohm. Trata-se, portanto, de um dipolo linear (pois tem dois polos).
No entanto, o filamento de uma lâmpada incandescente não segue esta característica. O que ocorre é que, quando o filamento está frio (contraído) sua resistência é menor. Assim, ao aplicarmos uma tensão, a corrente será intensa inicialmente, mas quando ele se dilatar, a corrente se reduz. Se fizermos um gráfico em que a corrente é mostrada em função da tensão, ele não será uma reta, como no caso de um resistor. Ele terá a aparência mostrada na figura 56.
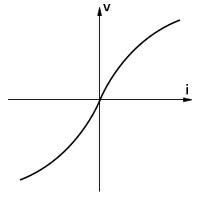
Este fato é muito importante em certas aplicações, onde devemos prever que ao ligar uma lâmpada, a corrente inicial é muito maior do que a corrente quando em funcionamento normal, ou seja, a corrente nominal.
O Conceito de Calor e Temperatura
Os conceitos de calor e temperatura são confundidos pela própria maneira como os usamos no dia a dia. Assim, é comum dizermos que está calor quando na verdade, o que ocorre é que a temperatura está elevada.
Quando tocamos em dois objetos percebemos facilmente pelo nosso tato que as suas temperaturas são diferentes. Esses objetos têm temperaturas diferentes porque seus átomos se agitam com intensidades diferentes. A temperatura nada mais é do que o grau de agitação dos átomos de um corpo.
Quando então constatamos que um corpo está com uma temperatura mais elevada do que outro é porque seus átomos se agitam com intensidades diferentes, conforme mostra a figura 57.
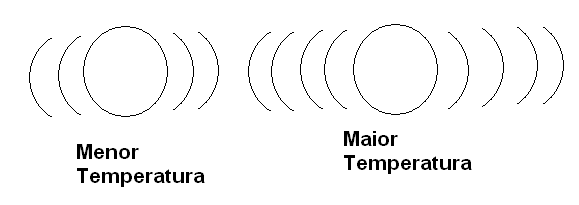
A agitação dos átomos se deve ao fato de que eles possuem energia cinética.
A quantidade de energia armazenada pelos átomos de um corpo nos permite associar outra grandeza que é o calor. Isso significa que precisamos entregar calor (energia) a um corpo para que seus átomos se agitem mais e, com isso, sua temperatura se eleve.
Veja que se entregarmos a mesma quantidade de energia a um corpo pequeno e a um corpo grande, a energia se distribui pelas partículas pelos dois e o menor vai se aquecer mais do que o maior, conforme mostra a figura 58.
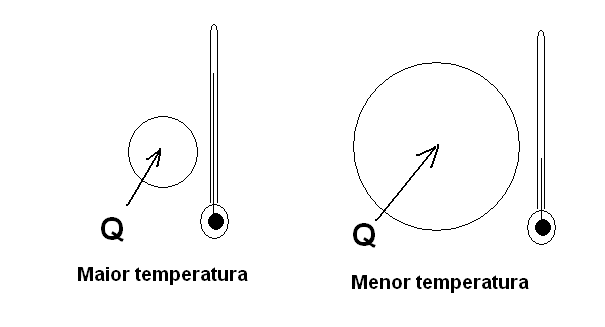
O leitor deve então entender que o calor é a energia que faz com que a temperatura de um corpo suba ou desça.
Quando um corpo recebe calor sua temperatura sobe. Quando ele perde calor sua temperatura baixa.
Em eletrônica a transferência de calor entre os corpos é muito importante, pois existem os casos em que aproveitamos o calor gerado pela energia elétrica, por exemplo, em sistemas de aquecimento, como casos em que precisamos nos livrar desse calor de modo que a temperatura de um componente não suba excessivamente e ele se queime.
Na prática o calor pode ser transferido de um corpo para outro de três formas.
a) Contato
Quando dois corpos são colocados em contacto, o choque das partículas de um com partículas do outro transfere a energia responsável pela agitação. Assim, se um corpo estiver com uma temperatura mais elevada (maior agitação e outro com temperatura menor (menos agitação), os choques tendem a equilibrar a agitação e com o tempo a temperatura dos dois se equilibra, conforme mostra a figura 59.
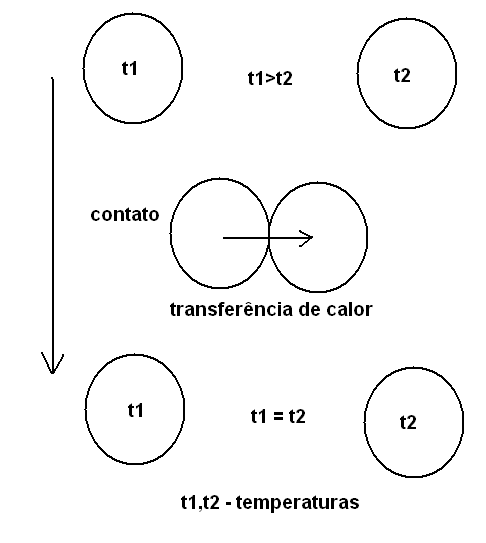
Convecção
O contato de um corpo aquecido com o ar faz com que ele transfira a energia de suas partículas na forma de agitação para ele. Dessa forma, com maior grau de agitação (maior temperatura) o ar se dilata, torna-se mais leve tendendo a subir. Forma-se então uma corrente de ar que sobe “levando” o calor gerado pelo corpo, conforme mostra a figura 60.
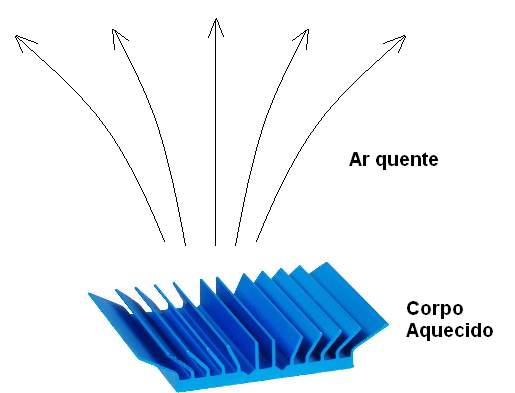
Radiação
A energia da agitação das partículas de um corpo pode ser irradiada na forma de ondas eletromagnéticas. Se for pequeno o grau de agitação, ela ocorre na forma de infravermelho, mas se a temperatura subir muito, ela ocorre na forma de luz visível, indo do vermelho, passando pelo branco e indo até a predominância do azul. É o que ocorre com um ferro em brasa ou o filamento de uma lâmpada.
Radiadores de calor
Conforme estudamos, todo dispositivo eletrônico, que não apresente uma resistência nula, gera certa quantidade de calor ao ser percorrido por uma corrente elétrica. Como o dispositivo de resistência nula é ideal, não existindo na prática, podemos dizer que todos os dispositivos percorridos por corrente num circuito real geram calor.
Para os casos em que o calor gerado é maior, precisando ser transferido para o meio ambiente, de modo que o componente não tenha sua temperatura elevada acima dos limites que ele tolera, devem ser usados meios auxiliares.
Assim, além de recursos que permitem espalhar o calor pela própria placa de circuito impresso, através dos materiais, a ventilação forçada, o principal meio, sem dúvida é o que faz uso dos radiadores ou dissipadores de calor.
Esses dispositivos são presos aos componentes que geram calor e por condução transferem esse calor para os elementos que devem passar o calor para o meio ambiente, conforme mostra a figura 61.
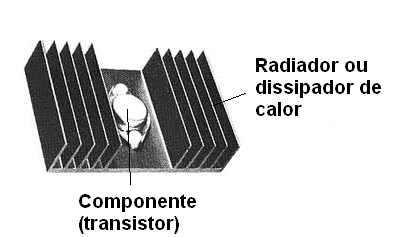
Essa transferência pode ser feita de duas formas basicamente: irradiação e convecção.
Parte do calor é irradiada na forma de ondas eletromagnéticas, concentrando-se principalmente na faixa dos infravermelhos. Parte-se das propriedades dos corpos negros que são irradiadores ideais, para se escolher materiais que possam ser usados de modo eficiente nesta forma de se livrar do calor gerado pelos componentes.
A outra parte do calor gerado é transferida para o ar em contacto com as aletas que os radiadores possuem, o qual aquecido torna-se mais leve tendendo a subir e se afastar do local, levando o calor absorvido. Neste caso, é muito importante que o dissipador tenha a maior área possível de contacto com o ar e que exista um caminho livre para sua circulação.
Na figura 62 mostramos os dois modos segundos os quais o calor é transferido para o ambiente através dos radiadores ou dissipadores de calor.
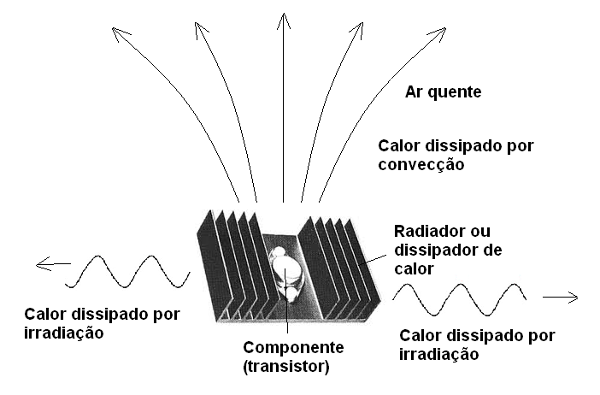
Veja que poderíamos falar numa terceira forma de se transferir o calor gerado, acoplando o próprio dissipador a uma superfície sólida que pudesse absorver o calor, mas neste caso, essa superfície é que deveria ser considerada como dissipador. Neste caso teremos a transferência de calor por contato.
Também devemos lembrar os casos em que a quantidade de ar em contacto com as aletas que devem transferir o calor pode ser sensivelmente aumentada com o uso de ventilação forçada, como ocorre no caso do uso dos “fans” (ventiladores ou ventoinhas), muito comuns em dispositivos que exigem uma grande taxa de transferência de calor, caso dos microprocessadores.
Zero Absoluto
Estudamos que a temperatura nada mais é do que a medida do grau de agitação das partículas de um corpo. Se partimos da temperatura ambiente, vemos que todos os corpos que nos cercam e que estão numa mesma temperatura têm suas partículas agitando-se da mesma forma.
Vamos agora supor que peguemos um objeto qualquer e o esfriemos gradualmente. Verificamos então que suas partículas vão vibrar cada vez mais intensamente até que chega um momento em que elas param.
Teremos então chegado à temperatura mínima possível, porque não existe movimento mais lento do que o parado. Esta paralisação, ou mínimo absoluto, ocorre com uma temperatura de -273º C, conforme mostra a figura 63.
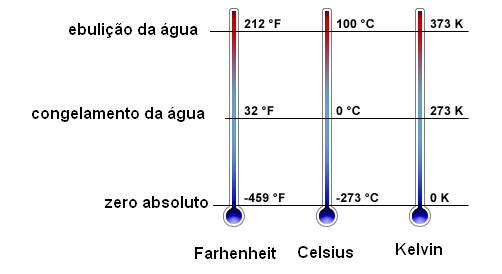
Uma forma mais correta de se medir a temperatura seria então colocar o zero grau neste ponto. Isso é feito na escala Kelvin (oK) ou de graus absolutos que é mostrada na figura 60. Ela parte o ponto em que temos a temperatura mínima possível e nos 273º K temos o correspondente ao 0o C.
Em muitas especificações eletrônicas e mesmo cálculos utiliza-se a temperatura em graus Kelvin (oK).
Lei de Joule
A quantidade de calor que um resistor produz quando percorrido por uma corrente é calculada pela Lei de Joule.
O que esta lei estabelece é que a quantidade de calor gerado, ou potência dissipada (medida em watts), é proporcional ao produto da corrente pela tensão no resistor, conforme a fórmula:
P = V x I (f3.4)
Onde:
P é a potência em watts (W)
V é a tensão em volts (V)
I é a corrente em ampères (A)
Levando em conta, pela Lei de Ohm, que a corrente num resistor é proporcional à tensão em seus terminais ou R = V/I , também podemos escrever para a Lei de Joule que:
P = R x I2 (f3.5)
P= V2/R (f3.6)
Exemplo de cálculo:
Calcular a potência dissipada por um resistor de 10 ohms quando ligado a um gerador de 12 volts.
Resolução: como temos dadas a tensão e a resistência, usamos a fórmula f3.6.
P = (12 x 12)/10
P = 144/10
P = 14,4 watts
Associação de Resistores
Os resistores podem ser ligados de diversas formas para ter seus efeitos combinados. Um conjunto de resistores ligados de determinada forma é denominado uma "associação de resistores".
Para o profissional da eletrônica (de outras ciências ligadas à eletricidade) é muito importante saber prever qual será o efeito final, ou seja, a resistência apresentada por um conjunto de resistores ligados de determinada forma.
Conforme o leitor verá, isso também é válido quando associamos outros tipos de componentes. Temos então os seguintes tipos de associações de resistores:
Associação de Resistores em Série
Quando ligamos resistores em série, conforme mostra a figura 64, a resistência resultante que obtemos equivale à soma das resistências dos resistores associados. Veja que ligar “em série” é fazer com que a mesma corrente passe por um após outro.
Nesse exemplo tomamos a associação de resistores de 10, 20 e 30 ohms, o que resulta numa resistência total de 60 ohms.
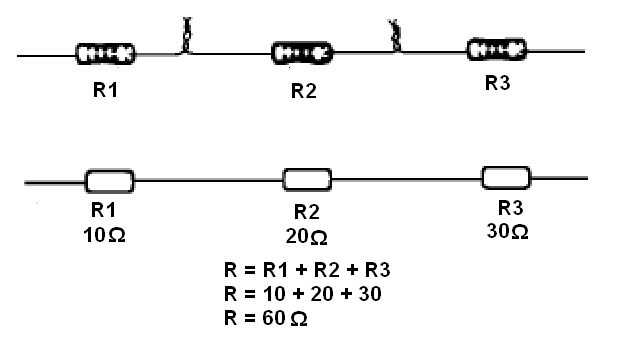
Podemos escrever a seguinte fórmula para o cálculo da resistência equivalente a uma associação de resistores em série:
R = R1 + R2 + R3 +......+ Rn (f3.7)
Onde: R é a resistência equivalente (em ohms)
R1, R2, R3....Rn são as resistências dos resistores associados (em ohms)
Propriedades da Associação Série:
1. Todos os resistores são percorridos pela mesma intensidade de corrente
2. O maior resistor dissipa mais calor
3. A resistência equivalente é maior do que a resistência do maior resistor associado
4. O maior resistor está submetido à maior tensão
Observe que para a última propriedade, se ligamos uma associação de resistores a uma fonte de tensão, a tensão dessa fonte ficará dividida proporcionalmente entre os resistores, conforme você pode na figura 65.
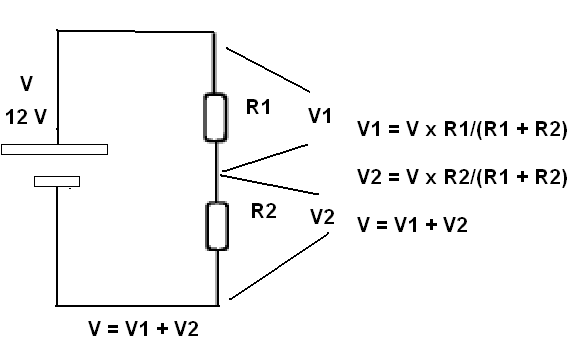
Essa propriedade é importante, pois nos permite usar resistores ligados em série como "divisores de tensão". Podemos obter tensões menores de um circuito, simplesmente escolhendo de forma apropriada os valores dos resistores que vamos ligar em série.
Na figura 66 temos um exemplo em que obtemos uma tensão de 8 V a partir de uma fonte de 12 V usando resistores.
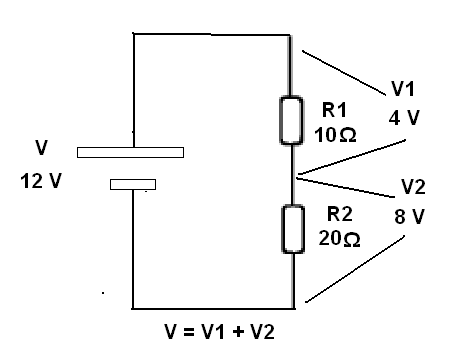
Evidentemente, o cálculo de um divisor pode ser um muito mais complicado na prática do que a simples divisão proporcional, pois temos de levar em conta a corrente que deve ser fornecida ao circuito que vai ser alimentado pelo divisor.
Associação de Resistores em paralelo
Numa associação de resistores em paralelo, os resistores são ligados conforme mostra a figura 67, um ao lado do outro. A corrente se divide através dos resistores na mesma figura.
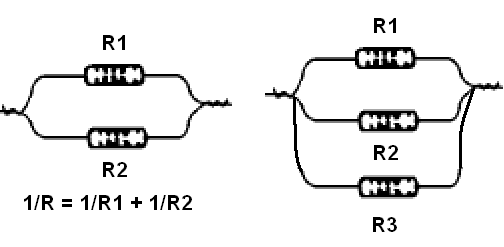
Na associação (ou ligação) em paralelo, a resistência equivalente é dada pela fórmula:
1 / R = 1 / R1 + 1 / R2 + 1/R3 + ........ + 1/Rn (f3.8)
Onde:
R é a resistência equivalente (em ohms)
R1, R2, R3 .... Rn são as resistências associadas ( em ohms)
Podemos dizer que "o inverso da resistência equivalente à associação de resistores em paralelo, é igual à soma dos inversos das resistências dos resistores associados".
Para o caso da figura 68, à resistência equivalente á ligação de um resistor de 20 ohms com um de 30 em paralelo é de 12 ohms.
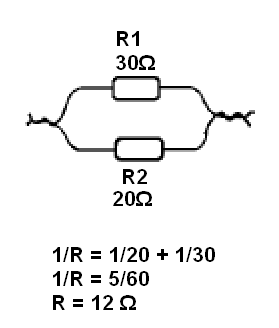
Caso especial:
Quando temos apenas dois resistores em paralelo, o cálculo da resistência equivalente pode ser simplificado pela fórmula:
R = (R1 x R2)/(R1 + R2)
Basta então multiplicar um resistor pelo outro e dividir pela soma. Por exemplo, 20 ohms com 30 ohms em paralelo resultam em:
a) 20 x 30 = 600
b) 600/ 50 = 12 ohms (50 = 20 + 30)
Propriedades da Associação Paralelo de Resistores
1 A corrente em cada resistor é inversamente proporcional ao seu valor. O menor resistor é percorrido pela maior corrente.
2 Todos os resistores estão submetidos à mesma tensão
3 O menor resistor é percorrido pela maior corrente e dissipa a maior potência
4 A resistência equivalente é menor do que a resistência do menor resistor associado.
Associação Série-Paralelo de Resistores
Existem associações de resistores mais complexas em que podemos encontrar alguns resistores ligados em série e outros em paralelos, de uma forma que não nos permite classificar o circuito num ou noutro grupo.
Assim, clicando na figura 69 vemos uma associação série-paralelo de resistores.
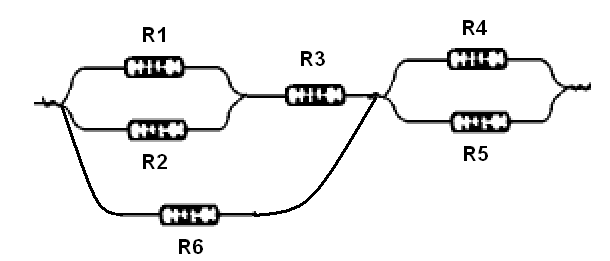
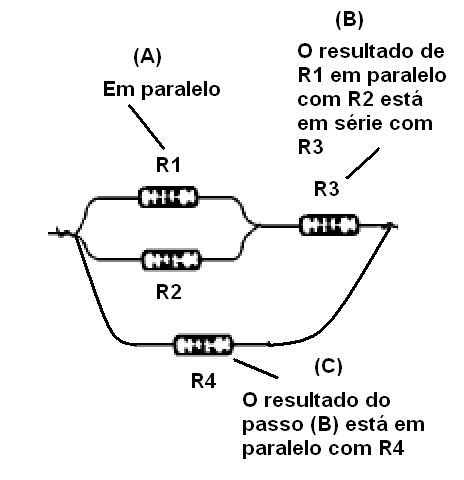
Para calcular a resistência equivalente trabalhamos por partes, calculando os grupos de resistores que podemos identificar como estando em paralelo ou série, conforme mostra a figura 70.
Potenciômetros e Trimpots
Existem aplicações em que é preciso contar com um componente que possa ter sua resistência modificada ou ajustada depois de instalado num circuito.
Esses componentes se enquadram no grupo dos resistores variáveis e os dois tipos mais encontrados são os potenciômetros e os trimpots. A palavra trimpot deriva de trimmer potentiometer ou potenciômetro ajustável.
Os potenciômetros e trimpots são dispositivos que podemos usar para variar a resistência apresentada à circulação de uma corrente elétrica.
Na figura 71 temos os aspectos mais comuns com que encontramos esses componentes, assim como seus símbolos.

Eles são constituídos por um elemento de resistência, que pode ser de carbono ou fio de nicromo, sobre o qual corre uma lingueta denominada cursor. Conforme a posição deste cursor temos a resistência apresentada pelo componente.
Veja que, tomando o potenciômetro ou trimpot da figura 72, à medida que o cursor vai de A para B, aumenta a resistência entre A e X ao mesmo tempo em que diminui a resistência entre X e B.
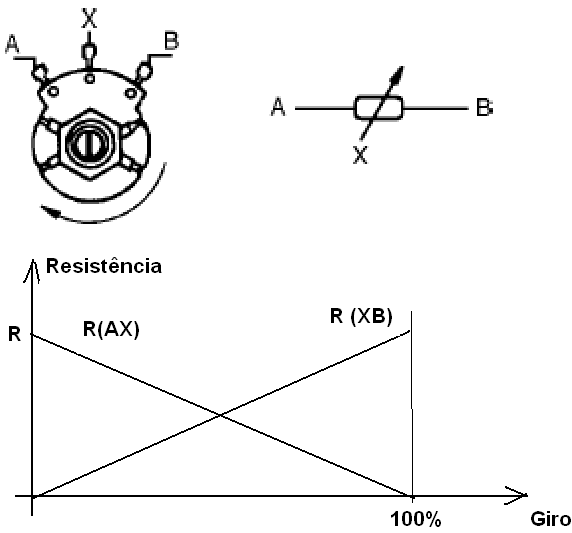
Se a resistência varia de forma proporcional ao movimento do cursor, temos um potenciômetro linear. Se a variação segue uma lei logarítmica, temos um potenciômetro logarítmico.
Essas características podem ser observadas pelas curvas dos dois tipos de potenciômetros mostradas na figura 73.
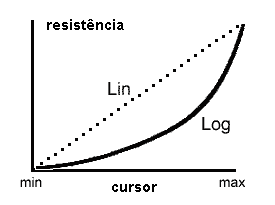
Observe que a resistência total, entre A e B é a resistência nominal do componente, ou seja, o valor máximo que podemos obter.
Na prática, podemos encontrar potenciômetros e trimpots com valores na faixa de fração de ohms até milhões de ohms. Se o mesmo eixo controlar dois potenciômetros, diremos que se trata de um potenciômetro duplo.
Alguns potenciômetros incorporam um interruptor que é controlado pelo mesmo eixo, como acontece com os controles de volume de rádios e amplificadores. No mesmo controle podemos aumentar e diminuir o volume e ainda ligar e desligar o aparelho, conforme mostrado na figura 74.
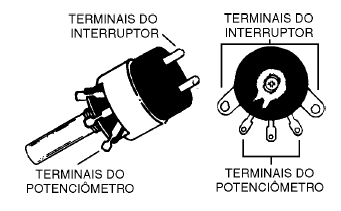
Os potenciômetros são usados em diversas funções como, por exemplo, controles de volume, controles de tonalidade, sensibilidade, brilho de uma lâmpada ou velocidade de um motor, já que permitem o ajuste, a qualquer momento, das características desejadas.
Já os trimpots são usados quando se deseja um ajuste único, ou seja, somente num determinado momento, levando o aparelho a um comportamento que deve ser definitivo (é claro que o ajuste pode ser refeito sempre que necessário, mas o trimpot normalmente fica dentro do aparelho, que nesse caso precisa ser aberto).
Na figura 75 mostramos trimpots de precisão, do tipo multivoltas, muito usados em instrumentos, equipamentos sensíveis e outros.

Transdutores e sensores
Os circuitos eletrônicos só podem trabalhar com sinais elétricos, ou seja, com correntes e tensões.
Assim, se precisarmos medir temperaturas, pressões, ou outras grandezas físicas que nada tenham a ver com eletricidade, precisamos convertê-las.
Da mesma forma, não vemos nem ouvimos a eletricidade, o que significa que existem aplicações em que precisamos converter energia elétrica em outras formas de energia como som, luz, etc.
Os dispositivos que convertem uma forma de energia em outra são denominados "transdutores". Como eles são usados para sensoriar determinadas grandezas, eles também são chamados sensores. Na figura 76 temos exemplos desses componentes.

Um tipo importante de transdutor é o que converte uma grandeza física qualquer numa resistência correspondente. Dizemos que se trata de um transdutor ou sensor resistivo, existindo diversos deles que são usados em equipamentos eletrônicos.
No próximo item vamos estudar diversos desses transdutores, que nada mais são do que resistores especiais, cuja resistência varia conforme uma determinada grandeza física.
LDR
Os LDRs ou Light Dependent Resistors são componentes cuja resistência depende da quantidade de luz que incide numa superfície sensível que possuem. O componente apresenta uma resistência muito alta no escuro (da ordem de milhões de ohms) e muito baixa no claro (da ordem de dezenas ou centenas de ohms). Os LDRs são usados em sensores de luz. Na figura A temos o aspecto de um LDR. A figura 77 mostra o símbolo adotado para representar esse componente e os aspectos mais comuns.
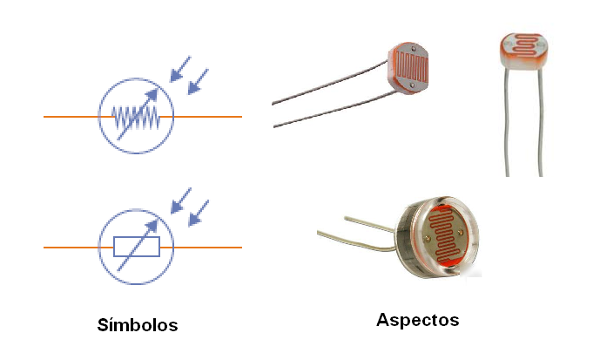
NTC/PTC
Os Negative Temperature Coefficient Resistors ou NTCs são componentes cuja resistência diminui com o aumento da temperatura. Por outro lado, os PTCs ou Positive Temperature Coefficient Resistors são componentes cuja resistência aumenta com o aumento da temperatura. Os dois podem ser usados como estabilizadores em circuitos sensíveis à variações de temperatura ou ainda como sensores de temperatura. Na figura 78 podemos ver esses componentes, seus aspectos e as curvas características.
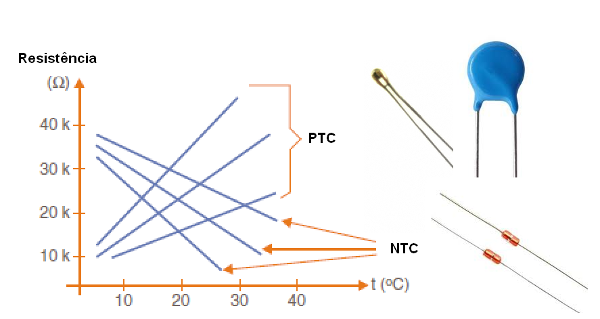
VDR
VDRs ou Voltage Dependent Resistors são resistores cuja resistência depende da tensão aplicada aos seus terminais. Os VDRs são usados basicamente como protetores contra surtos e transientes em circuitos eletrônicos, desviando pulsos de alta tensão que poderiam danificar os equipamentos. Na figura 79 temos o símbolo e os aspectos desse componente.

Além desses transdutores existem outros que serão estudados oportunamente dadas suas importâncias apenas em aplicações específicas.
Em muitos equipamentos das últimas gerações, que fazem uso de tecnologia digital, o tradicional potenciômetro de carvão ou fio está sendo substituído pelo potenciômetro digital. Esses potenciômetros não possuem partes móveis. A resistência apresentada entre dois terminais depende de uma programação digital aplicada a pinos de controle.
As lições deste curso são:
Lição 1 – Matéria e energia, a natureza da eletricidade, eletricidade estática
Lição 2 – Energia elétrica, corrente e tensão. O circuito elétrico
Lição 3 – Resistência elétrica, resistores, Lei de Ohm, Lei de Joule
Lição 4 – Tipos de geradores, rendimento e equação do gerador
Lição 6 – Magnetismo e eletromagnetismo
Lição 9 – Ondas eletromagnéticas



















