A unidade decibel, ainda que importante no campo da eletricidade, é pouco conhecida, teoricamente, por todos àqueles que, de uma ou outra forma lidam com eletrônica e/ou telecomunicações. Não se pretende com este trabalho por um término às dificuldades nem tampouco expor toda a complexa teoria do decibel e sim, fornecer elementos básicos para um justo e perfeito entendimento desta unidade.
Aquilino R. Leal
A maioria dos dispositivos em eletricidade podem ser considerados como quadripolos que nada mais são do que redes com dois acessos de entrada e outros dois de saída; normalmente, um acesso é comum tanto à entrada como à saída — figura 1 (B) — é o caso do transistor por exemplo — figura 2.
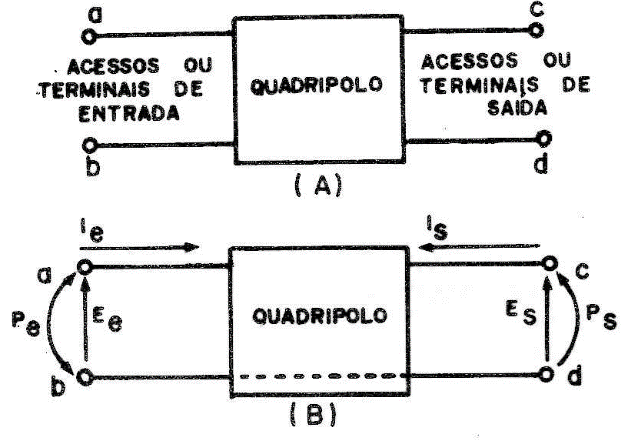
Ie - CORRENTE DE ENTRADA;
Is - CORRENTE DE SAÍDA;
Ee - TENSÃO DE ENTRADA;
Es - TENSÃO DE SAÍDA;
Pe - POTÊNCIA DE ENTRADA;
Ps - POTÊNCIA DE SAÍDA.
Os quadripolos são constituídos por circuitos elétricos tanto ativos como passivos. Os quadripolos ativos fazem com que a potência de saída Ps seja maior que a de entrada Pe enquanto nos passivos ocorre o contrário, isto é: Ps Pe.
Os quadripolos que aumentam a intensidade de potência produzem o que se denomina de ganho enquanto a perda de potência, característica dos quadripolos passivos, é chamada atenuação.
Consideremos o quadripolo mostrado na figura 1(A). Suponhamos diferentes quantidades de potência de sinal aplicadas aos terminais de entrada a e b desse quadripolo e que as potências correspondentes que surgem nos terminais de saída c e d sejam medidas, fornecendo os resultados mostrados na tabela I seguinte.

Dessas quantidades, as perdas absolutas de potência no quadripolo podem ser determinadas como a diferença entre as potências de entrada e as potências de saída, como mostrado na tabela II.

É evidente que a característica de atenuação do quadripolo não pode ser definida univocamente em termos de perda absoluta de potência porque a quantidade de potência perdida depende da quantidade de potência introduzida nos terminais de entrada; para um dado valor de potência de entrada, digamos, de 15 mW será trabalhoso determinar a perda de potência bem como calcular a potência de saída do quadripolo. Observamos, no entanto, que a relação entre a potência de saída e a potência de entrada permanece constante, como se pode verificar na tabela II.
Observa-se que o fator de atenuação do sistema como um todo pode ser determinado multiplicando-se os fatores de atenuação dos quadripolos individuais que constituem o sistema, isto é:
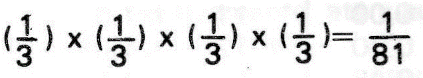
Portanto, o favor de atenuação de qualquer sistema, ainda que complexo, poderá ser determinado multiplicando-se os fatores de atenuação dos componentes individuais que compreendem o sistema, ou seja
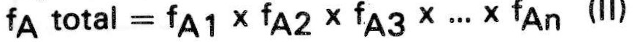
A relação entre a potência de saída e a potência de entrada (Ps/Pe) proporciona, portanto, uma caracterização da atenuação do quadripolo; podemos dizer então que o fator de atenuação (fA) no nosso caso é 1/3, representando que o valor da potência de saída é sempre a terça parte do valor da potência de entrada. Para o caso anterior dos 15 mW de entrada, poderemos garantir que a potência de saída será de 15 mW 4- 3 = 5 mW enquanto a perda de potência será de 15 mW - 5 mW = 10 mW.
O fator de atenuação de qualquer quadripolo pode ser definido como:
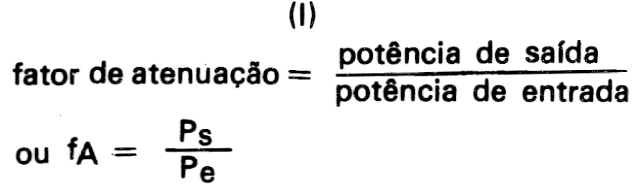
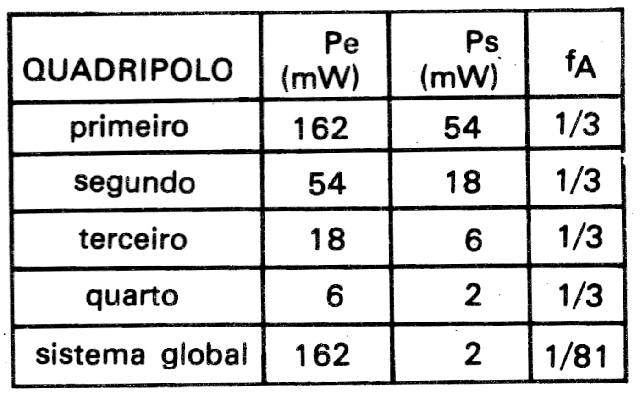
Caso tivéssemos quatro desses quadripolos ligados conforme mostra a figura 3 e, se forem aplicados aos terminais de entrada a1 b1 uma potência de 162 mW, os níveis de potência nos vários pontos do sistema assim constituído, seriam os mostrados na tabela IV.

É óbvio que o fator de atenuação é uma grandeza adimensional sempre menor que a unidade, como vimos nos exemplos anteriores; tratando-se de ganhos, o fator, que no caso é de ganho, é sempre maior que a unidade. Quando não houver nem ganho nem atenuação propriamente ditos, isto é, quando o valor da potência de saída for igual ao da entrada, o fator de atenuação é unitário.
O procedimento acima para determinar o fator de atenuação do sistema global pode tornar-se enfadonho se um grande número de componentes (quadripolos) estiver envolvido. Por esta razão, a definição dada acima é modificada usando uma ferramenta matemática denominada logaritmo. Algumas propriedades mais importantes dessa ferramenta matemática serão recordadas antes de passarmos ao estudo da unidade decibel propriamente dita.
O logaritmo nada mais é do que uma função matemática por meio da qual um dado conjunto de números positivos é transformado num outro conjunto numérico relacionado com o primeiro, ou seja: para todo número positivo N existe um outro número n, positivo, negativo ou nulo, tal que n é o logaritmo de N na base 10, que se escreve:
Usualmente a base 10 é omitida, ou seja:
n = log N (IV)
Das propriedades mais importantes para dos logaritmos as mais importantes para o nosso estudo são:
log 1 = 0 (V)
log 10 = 1 (VI)
log 10m = m (VII)
log Nb = b.log N (VIII)
log (A/B ) = log A - log B (IX)
log (A x B) = log A + log B (X)
Pois bem, o fator de atenuação definido I é agora redefinido como:
fator de atenuação = log (potência de saída / potência de entrada) ou
fa = log (P1/Pe) (XI)
O fator de atenuação para cada um dos quadripolos do exemplo anterior torna-se, então:
fa = log (1/3)
e o do sistema global torna-se:
fa = log (1/81) ou, o que é a mesma coisa:
fa=log (1/3 x 1/3 x 1/3 x 1/3)
de acordo com a expressão X vê-se que
fa = log 1/3 + log 1/3 + log 1/3 + log 1/3
Então, temos agora um método pelo qual o fator de atenuação global de um sistema complexo pode ser determinado somando--se os fatores de atenuação (fa) individuais em vez de multiplicá-los como sucedia para os fatores de atenuação designados por fa. Isto acarreta uma simplificação nos procedimentos de cálculo.
Tendo em mente que a relação de potências é um número positivo, o fator de atenuação é, portanto, um número fixo definido por
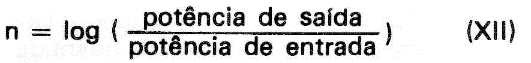
A unidade associada a n é o "Bel". Na maioria das aplicações o Bel é uma unidade muito grande para representar atenuações ou ganhos e, por isto, é dividida em dez partes iguais; cada uma dessas partes denomina-se "decibel" sendo abreviada por dB, então, empregando a letra grega alfa, simbolizada por x , para designar o fator de atenuação, temos:

As tabelas dos logaritmos encontram-se em qualquer bom livro de matemática ou podem ser obtidos através de uma das minicalculadoras eletrônicas modernas. A título de ilustração foram tabelados os logaritmos de alguns números inteiros — tabela V.
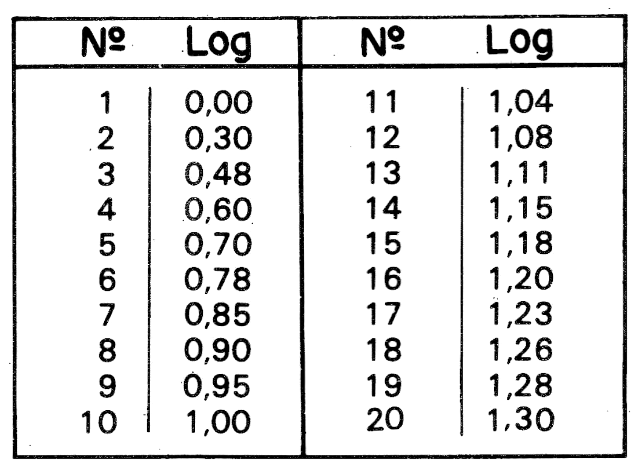
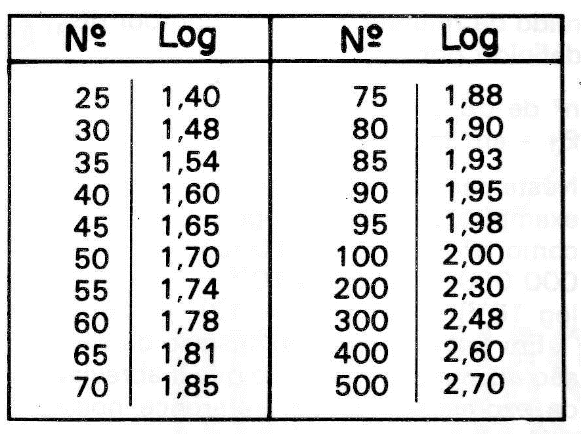
Para o exemplo dado, a atenuação dos quadripolos componentes da figura 3 e, de acordo com a tabela V é:
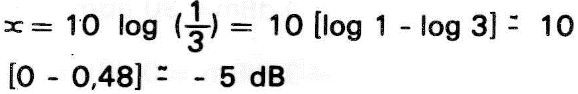
Do mesmo modo, a atenuação global do sistema é:
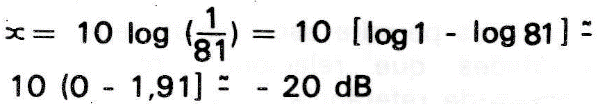
Observamos que se somando as atenuações dos componentes individuais encontramos a atenuação global do sistema. Outra particularidade é a que, quando, a potência de saída for menor que a de entrada o resultado, em dB, é negativo; isto indica uma perda de potência. Quando a potência de saída for maior que a de entrada o resultado calculado é positivo, indicando um ganho de potência, no entanto é evidente que duas quantidades fixas de potência formam sempre o mesmo valor absoluto em dB em virtude da propriedade IX dos logaritmos, apenas o sinal negativo é omitido, sendo substituído pela expressão "atenuação". Nos dois casos anteriores, por exemplo, costuma-se dizer, respectivamente, atenuação de 5dB e atenuação de 20dB.
Outra vantagem de se usar a unidade decibel é a de reduzira incômoda faixa de números associados a relações de potência a números muito mais convenientes, portanto, mais fáceis de serem manuseados. Por exemplo, os níveis de potência típicos dos sinais transmitidos através de uma rede telefônica são da ordem de 0,001W enquanto as potências de ruído que tendem a interferir com os sinais telefônicos são da ordem de 0,000 000 000 001 W; a relação entre essas duas quantidades (relação sinal-ruído) de potências é:
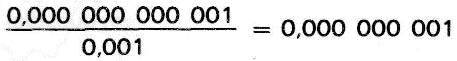
usando no entanto a unidade decibel vem:
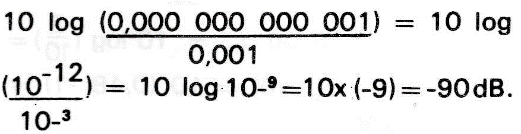
Convenhamos que é muito mais cômodo a manipulação do número -90 (dB) do que 0,000 000 001.
O decibel foi definido como uma relação entre potências e por esta razão o mesmo não mede potências e sim fornece a relação entre duas potências quaisquer, isto é, a relação decibel é simplesmente uma declaração de quanto a potência de um ponto de circuito excede a potência de um outro ponto.
As aplicações de transmissão telefônica, entre outras, geralmente não se preocupam com a diferença entre dois níveis arbitrários de potência, mas sim com a diferença entre um dado nível de potência e alguma potência de referência fixa.
A diferença a que nos referimos pode ser determinada pela generalização da equação XIII: a diferença entre dois níveis de potência P1 e P2, em dB, é:
n° de dB = 10 log (P1/P2) (XIV)
em que P1 e P2 são potências expressas numa mesma unidade.
Fixando convenientemente o valor de P2 poderemos expressar a potência P1, em termos de decibéis, por intermédio da relação anterior. Este valor nos dirá quantas vezes, logarítmicamente, P1 será maior que P2 pré-fixada.
O valor de P2 como dissemos, irá depender da aplicação. Para aplicações que empregam níveis altos de potência faremos a potência de referência — P2 — ser igual a 1W; neste caso a potência P1 é dita estar "tantos dB acima de um watt", abreviado dbW, isto é:
n° de dBW = 10 log P1 (XV)
P1 — em watts.
Assim, se num dado ponto de um dispositivo tivermos uma potência de, digamos, 4W, vem: n° de dBW= 10 log 4 =10 x 0,60 = 6dbW ou seja: a potência no ponto em pauta está 6dB acima de um watt ou, o que é a mesma coisa: a potência do ponto em questão é de 6dBW.
Se no mesmo ponto tivéssemos uma potência de 0,3W, teríamos:
n° de dBW = 10 log 0,3 = 10 log (3/10 ) = = 10 [log 3- log 10] = 10 (0,48 -1) = - 5,2 dBW.
O sinal negativo indica que a potência no ponto é menor que um watt e que a mesma se encontra a 5,2 dB abaixo de um watt ou, ainda, a potência no ponto em questão é de - 5,2 dBW.
Outra unidade comum relacionada com o decibel é obtida ao se fazer com que a potência de referência — P2 — assuma o valor de 10-3 watts (um miliwatt). Neste caso, a potência P1 é dita ser "tantos dB acima de um miliwatt",, abreviado dBm; isto é:
n° de dBm = 10 Iog P1
P1 — em miliwatts. J
Exemplificando: se P1 = 4W, esta potência pode ser expressa como:
n° de dBm = 10 log 4000 = 10 x 3,60 = 36 dBm
lembrar que 4W = 4000 mW.
Outra unidade que é aplicada em transmissão é obtida assumindo-se uma potência de referência de 10-8 watts (um microwatt). Uma potência P1 é dita, então, "tantos dB acima de um microwatt", abreviando-se por dBmw e dada por: n° de
dBmw = 10 logo (XVII)
P1 – em microwatts
Para o exemplo acima teremos:
P1 = 4 W = 4000 miliwatts = 4000 000 microwatts então:
n° de dBmw = 10 log 4 000 000 = 10 log 4.106 = 10 [log 4 + log106]= 10 (0,60 + 6) = 66 dBmw.
Como geralmente as potências de ruído ("noise" em inglês) são da ordem de 10-12 watts (um picowatt) se torna isto como referência para potências de ruídos então, P1 pode ser expressa em "dB acima do ruído de referência", abreviado por dBnr e definido por:
n° de dBnr = 10 log P1 (XVIII)
P1 - em microwatts.
Neste caso o nível de potência de 4W dos exemplos precedentes pode ser expresso como n° de dBrn = 10 logo 4 000 000 000 000= 10 Iog 4.1012 = 10 [ log 4 + Iog 1012] = 10 (0,60 + 12) = 126 dBrn
Em tempo: o "rn" minúsculo da expressão dBrn nada mais é do que a abreviatura da expressão inglesa "reference noise" -ruído de referência.
De acordo com as expressões XV e XVIII têm-se as seguintes correspondências:
1 W ?O dBW = 30 dBm 60 dBmw = 120 dBrn
1mW ? -30dBW = O dBm= 30 dBmw 60 dBrn
1µW ? -6OdBW = -30dBm = O dBmw = 30 dBrn
1 pW ? -120dBW = -60dBm = -30dBmw = OdB rn
Isto nos permite escrever as seguintes igualdades que relacionam os quatro decibéis de referência definidos anteriormente.
xdBW = (x+ 30 dBm)= (x+ 60) dBmw= (x +120) dBnr (XIX)
A corrente e a tensão também podem ser relacionadas logarítmicamente da mesma forma que as potências. Considerando um quadripolo cujas impedâncias de entrada e saída sejam iguáis tanto em módulo como em ângulo de fase, poderemos escrever, a partir da expressão XIII, levando em consideração que:

As duas expressões acima mostram claramente que o ganho em tensão ou em corrente é numericamente igual ao dobro do ganho de potência do quadripolo em questão....




















