São dezenas os tipos de capacitores que encontramos nos circuitos eletrônicos, com as mais diversas finalidades. Os técnicos quase mecanicamente sabem como um capacitor funciona em determinada aplicação e quando devem substituí-los, mas certamente poucos são os que pararam para analisar como estes peque-nos dispositivos armazenam energia. Neste artigo abordaremos este interessante assunto de interesse para os principiantes, estudantes e técnicos.
Nota: Este artigo dos anos 80 saiu em publicação. Usei meu pseudônimo J. Martin nele.
Duas armaduras (condutores) separados por um meio isolante formam um capacitor (figura 1). O tipo de material usado como isolante dá nome a um capacitor, assim podemos ter capacitores de mica, papel, poliéster, cerâmica quando são estes os materiais usados como isolantes.
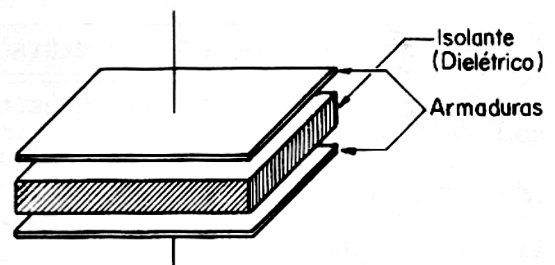
Na prática da eletrônica, o técnico encontrará diversos tipos de capacitores com formatos e capacitâncias numa ampla faixa de valores. Para cada aplicação, temos tipos recomendados em vista das propriedades tanto dos materiais usados como isolantes, denominados dielétricos, como também da própria construção.
Mesmo com características diferentes nos circuitos eletrônicos, a finalidade de um capacitor é sempre a mesma: armazenar cargas elétricas.
Como um capacitor faz isso, é o que veremos a seguir. Um capacitor tubular, ou seja, feito com as armaduras enroladas, como mostra a figura 2 de modo a se obter maior capacitância num volume reduzido, não se presta para aplicações que envolvem sinais de frequências elevadas. Isso ocorre porque, enrolando o material que forma as armaduras, normalmente tiras de alumínio, formamos uma bobina que passa a manifestar uma certa indutância. Se a frequência for alta esta indutância chega a predominar sobre a capacitância, e o componente que deveria ser um simples capacitor comporta-se na realidade como um misto de capacitor e indutor.
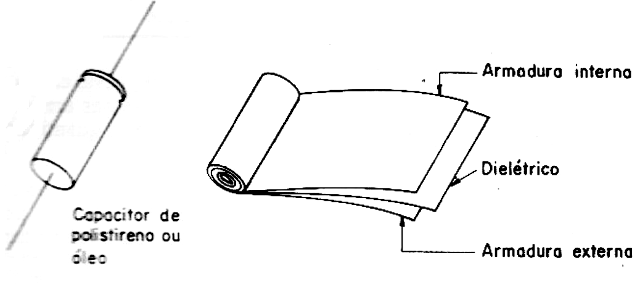
Os capacitores de poliéster metalizado, mesmo que de construção plana, também não servem para aplicações de frequências elevadas (circuitos de RF), pois o material isolante é que no caso não apresenta propriedades próprias para isso.
Já os capacitores cerâmicos tipo plate, disco ou mesmo tubulares já têm uma série de características que permitem sua utilização sem problemas em circuitos de frequências elevadas.
Armazenamento de energia
Se ligarmos um gerador às duas armaduras de um capacitor, conforme mostra a figura 3, uma certa quantidade de cargas fluirá e ficará nas armaduras em questão, carregando o capacitor.
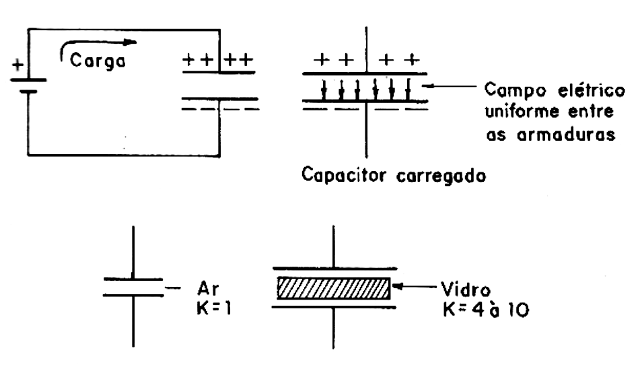
A quantidade de cargas positivas de uma armadura será exatamente a mesma quantidade de cargas negativas da outra armadura.
Se desligarmos o gerador, estas cargas serão mantidas na armadura pelas forças de atração eletrostática que se manifestam. A intensidade destas forças depende não só da separação das armaduras como também da natureza do material que existe entre elas, ou seja, o dielétrico.
Existem materiais em que as linhas de força podem atuar de uma maneira mais forte, polarizando suas moléculas e, com isso, a intensidade do campo será mais forte. Se usarmos um material deste tipo num capacitor, poderemos multiplicar a quantidade de cargas armazenadas. (figura 3).
Colocando uma folha de vidro entre as armaduras de um capacitor podemos aumentar em 4 a 10 vezes a sua capacitância, ou seja, a quantidade de cargas que ele pode armazenar.
Cada material possui uma "constante dielétrica" que justamente diz de que modo ele pode ser usado para multiplicar a capacitância de um capacitor em relação ao vácuo cuja constante é 1.
Damos a seguir uma tabela de constantes dielétricas de materiais comuns:
Baquelite - 4
Betume - 93
Celuloide - 3,5
Ebonite - 4
Vidro - 4 a 10
Mica - 4,5 a 8
Parafina - 2,2
Porcelana - 6,5
Poliestireno - 2,5
Borracha-2,6
O importante é que, neste campo elétrico que retém as cargas nas armaduras, está armazenada uma certa quantidade de energia.
Podemos comparar este campo a uma mola contraída que retém energia potencial e pode ser usada para alimentar um circuito externo.
De fato, quando ligamos um capacitor carregado a um circuito externo, um resistor, por exemplo, conforme mostra a figura 4, fluem as cargas com a diminuição gradual das linhas do campo (que se enfraquece). A corrente produz então calor que é a energia armazenada no capacitor que se dissipa.
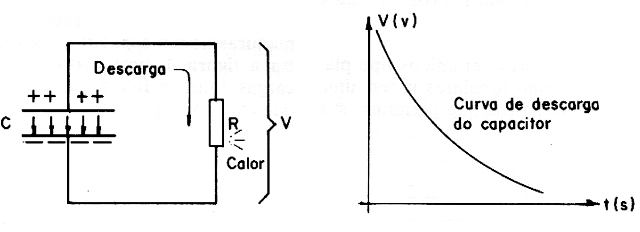
Podemos calcular exatamente as quantidades de energia envolvidas neste processo de uma maneira relativamente simples:
A capacitância (C) de um capacitor pode ser definida como a relação carga (Q)/tensão (V), que deve ser constante.
Se um capacitor armazena uma carga de 1 coulomb sob tensão de 1 volt, dizemos que ele tem uma capacitância de 1 farad.
C = Q/V (1)
Na prática, trabalhamos com capacitâncias muito menores que 1 Farad, preferimos usar os submúltiplos como o mIcrofarads (milionésima parte de 1 farad abreviado por µF), o nanofarad (bilionésima parte de 1 farad, abreviado por nF) e o picofarad (trilionésima parte de 1 farad, abreviado por pF).
O gráfico da figura 5 nos mostra que a relação Q/V se mantém constante na carga de um capacitor. Assim, se fizermos um gráfico que representa o aumento da quantidade de cargas nas armaduras de um capacitor em função da tensão que as "bombeia" veremos que ele corresponde a uma reta.
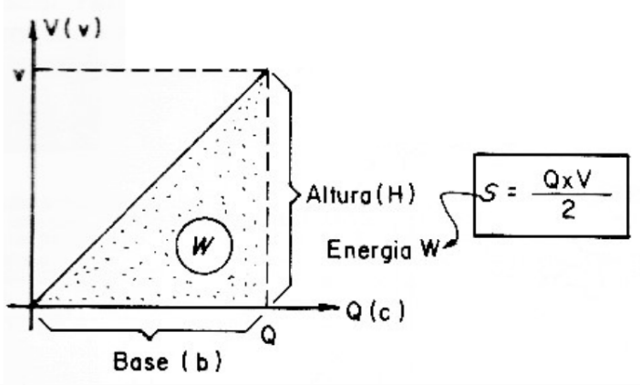
A área sobre esta reta representa a quantidade de energia que temos de gastar para --bombear" as cargas para as armaduras e, portanto, a energia "W" que o capacitor armazena.
Como a figura que temos, que corresponde à energia é um triângulo, sua área pode ser calculada pela fórmula:
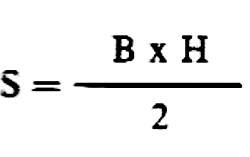
Onde S é a área; B a base e H a altura.
No nosso caso, a base é Q, ou seja, a quantidade de cargas armazenadas; V é a fia, ou seja, a tensão aplicada em volts.
Nossa fórmula ficará então como:
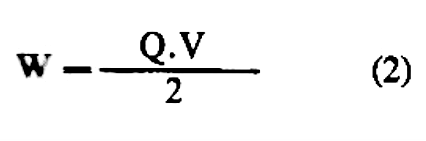
Em suma, para calcular a energia armazenada (em joules —J) multiplicamos a carga pela tensão e dividimos o valor encontrado por 2.
Na prática seria melhor trabalhar com a capacitância e não com a carga, já que esta é um valor que normalmente não nos é disponível de imediato num capacitor.
Como a relação C=Q/V é constante, podemos usá-la para substituir na fórmula (2).
Assim: Q = C x V
Substituindo em (2)
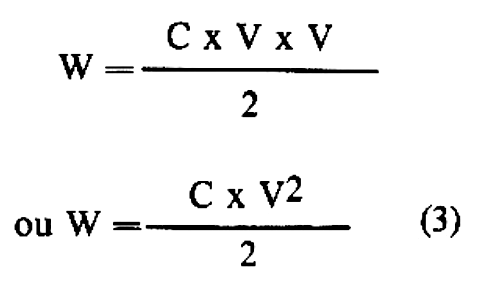
Sem dúvida, esta fórmula é bem melhor para calcular na prática quanto de energia armazena um capacitor. Tomemos um exemplo:
Exemplo de cálculo
Vamos supor que desejamos calcular a energia armazenada num capacitor de 100 µF quando o submetemos a uma tensão de 250V.
Neste caso:
C = 100 µF = 100 x 10-6 F
V = 250 V
Aplicando a fórmula (3):
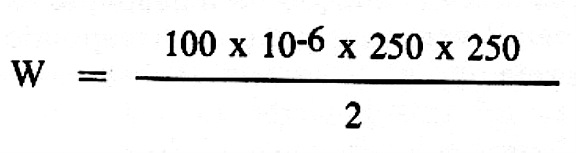
W = 6,25 Joules.
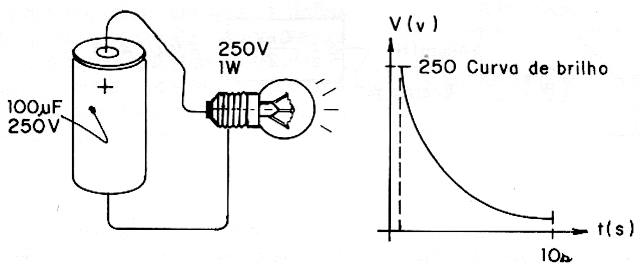
Se o leitor levar em consideração que 1 joule por segundo corresponde a 1 watt, a "enorme" carga armazenada neste capacitor acenderá uma lâmpada de 1 watt por apenas 6,25 segundos! Sem dúvida, os capacitores realmente armazenam energia, mas uma quantidade que não nos permite usá-los como fontes de energia de larga escala! Os capacitores armazenam pequenas quantidades de energia apenas, mas com muito proveito para os circuitos eletrônicos. (figura 6).
Conclusões
Veja que, na fórmula, a tensão aparece com o expoente 2 enquanto a capacitância não. Isso significa que podemos obter mais energia com tensões mais altas e não com capacitâncias mais altas. Assim, obtemos muito mais energia armazenada de um capacitor de 10 µF carregado com 100 volts do que de um capacitor de 100 µF carregado com 10 volts!
É claro que a tensão máxima que podemos aplicar a um capacitor tem limite, dado pelas características do dielétrico.
Concluímos então que, mesmo que na prática o capacitor não seja um dispositivo indicado para funcionar como reservatório em grande escala de "eletricidade", na eletrônica, onde fenômenos transitórios de curta duração precisam ser trabalhados, as pequenas energias envolvidas podem perfeitamente estar dentro daquilo que capacitores relativamente pequenos podem manusear, daí sua ampla gama de aplicações práticas.




















