MSc. Eng. Antonio Carlos Gasparetti.
 Este artigo foi escolhido e publicado na edição de número 4 da Revista INCB Eletrônica - Clique aqui e leia a revista completa
Este artigo foi escolhido e publicado na edição de número 4 da Revista INCB Eletrônica - Clique aqui e leia a revista completa1. O que é computação analógica
Computação analógica recebe este nome por trabalhar por analogia ou relação sistemática, entre os processos físicos no computador e aqueles no sistema que se pretende para modelar ou simular (o sistema primário). Por exemplo, as grandezas elétricas tensão, corrente e condutância podem ser usados como análogos da pressão do fluido, taxa de fluxo e diâmetro do tubo. Mais especificamente, na computação analógica tradicional, os valores resultantes do cálculo obedecem às mesmas leis matemáticas que as quantidades físicas no sistema primário. Assim, as quantidades computacionais são proporcionais às quantidades modeladas. [2]
O computador analógico é baseado em circuitos os quais podem calcular ou processar medidas, grandezas ou funções contínuas no tempo. Dentre tais circuitos analógicos, os baseados em amplificadores operacionais podem ser usados ??para implementar funções matemáticas sendo também úteis em muitas aplicações devido às suas características técnicas e funcionais.
Ao entrarmos em contato com as palavras "computador" ou "computação", normalmente associamos a sistemas digitais. Atualmente faz sentido, uma vez que a grande maioria dos sistemas computacionais operam baseados em estrutura binária e discreta. No primeiro momento, dada a grande vantagem dos sistemas digitais em vários quesitos, a computação analógica acabou sendo esquecida.
Porém, antes da computação digital se tornar algo comum, a computação analógica era largamente usada para aplicações em cálculos e solução de funções bem definidas, como soma, subtração, multiplicação, divisão, valor absoluto, máximo / mínimo, RMS, pico, raízes quadradas, quadratura, derivadas, exponenciais e integrais. [1]
Verificou-se ao longo do tempo que a computação analógica ainda tinha seu espaço no meio acadêmico e em pesquisas científicas específicas, onde suas características ainda tinham espaço para contribuir, uma vez que ela pode escapar de limitações da computação digital.[2]
Recentemente, pesquisas sobre computação não tradicional (também referenciada como não convencional ou exótica) estão ocorrendo em física de materiais, química, em ramos mais “exóticos” como biologia e ciências da vida.[3]
Estes aspectos tornam muito interessante revisitar os fundamentos e as origens da computação analógica e a participação em suas realizações. Basta lembrar que a régua de cálculo (slide rule) é um exemplo de computador analógico, a qual participou de inúmeros projetos de engenharia, aeroespaciais e até mesmo participando da missão Apollo 11 no pouso do homem na Lua. Nas páginas do Instituto Newton C. Braga, sobre computação analógica [4], o leitor poderá encontrar muitas informações sobre este tema. A figura 1 mostra um computador analógico.

2. História da computação analógica da era eletrônica
Computadores eletrônicos analógicos tornaram-se viáveis ??após a invenção do amplificador operacional DC. Cientistas da década de 1930 da Bell Telephone Laboratories (BTL) desenvolveram o amplificador de acoplamento DC, estabilizado por feedback, que é a base do amplificador operacional. Logo os engenheiros das décadas de 1940 viram aplicações da computação analógica eletrônica para aplicações militares e para a aplicação em pesquisa e ciência, dando origem ao GPAC – General Purpose Analog Computer ou Computador Analógico para Aplicações Gerais, também chamado de "Gypsy", concluído em 1949. Com base no design do amplificador operacional da BTL, trabalhos nesta plataforma computacional foram conduzidos na Universidade de Columbia na década de 1940. Em particular, esta pesquisa mostrou como a computação analógica poderia ser aplicada à simulação de sistemas dinâmicos e à solução de equações não lineares.[2]
3. Como funciona um computador analógico baseado em amplificadores operacionais.
Um computador analógico consiste em um conjunto de circuitos modulares capazes de individualmente realizar operações tais como soma, escalonamento, integração ou multiplicação de tensões. Estes conjuntos são interligados a módulos geradores de funções. Tais circuitos são compostos de amplificadores operacionais os quais podem ser arranjados com suas configurações em dezenas ou centenas de módulos formando um grande computador analógico.
Para resolver um determinado problema onde as quantidades físicas variam com o tempo, podemos representar tal problema através de equações diferenciais. A solução destas equações é realizada através da interconexão de módulos de circuitos analógicos com as suas entradas e saídas interconectadas de forma apropriada, incorporando escala, realimentação e definição das condições iniciais conforme necessário, com tensões representando as variáveis do modelo físico [5].
Assim, equações simples ou simultâneas podem ser resolvidas em tais aplicações em engenharia e cálculo científico, modelagem e simulação. A interconexão e definição de coeficientes e condições iniciais necessários são normalmente feitos por meio de um painel de interligações (patch panel) e potenciômetros. Como entrada utilizam-se geradores de função. Como saída, utiliza-se osciloscópios e/ou um gravador de dados.
Ao se utilizar o computador analógico para a pesquisa ou desenvolvimento, o projetista pode optar em observar imediatamente o efeito ao se modificar as tensões correspondentes aos parâmetros matemáticos através dos respectivos potenciômetros ou chaves. Em simulações as saídas do computador analógico podem ser usadas como tensões de entrada para outro sistema eletrônico o qual pretende-se controlar.[5]
3.1 Operadores aritméticos e de funções matemáticas
Os blocos básicos dos operadores matemáticos em um computador analógico são: Somadores, Inversores, Multiplicadores, Divisores, Integradores e diferenciadores. (Figura 2)
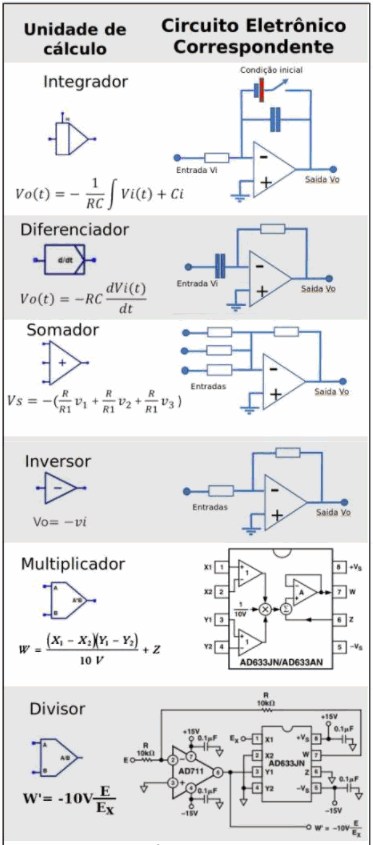
Cada bloco, ao receber sinais em suas entradas, processa tais sinais de forma a gerar sinais de saída correspondentes à operação matemática. Estes sinais, no caso tensões, deverão representar em seus valores às grandezas previamente identificadas e pertencentes ao modelo físico. Na figura 3 temos os equivalentes eletrônicos aos blocos de um computador analógico.
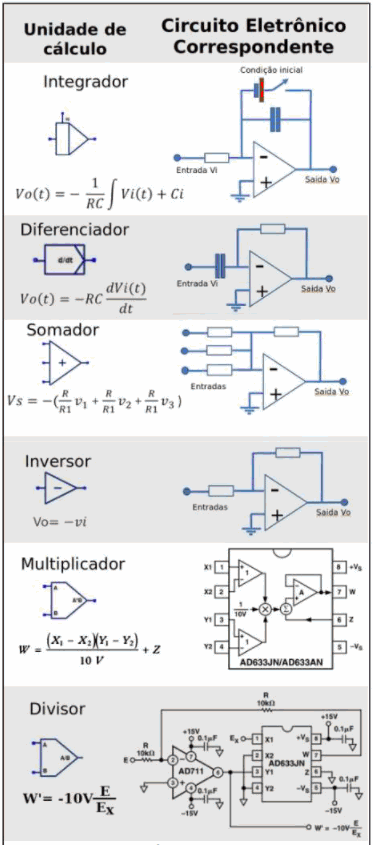
4. Exemplo de um computador analógico e a aplicação em um sistema dinâmico
O comportamento de fenômenos físicos, químicos, biológicos que variam no tempo podem ser descritos através de modelos matemáticos os quais ligam o estado presente aos estados passados, representados por sistemas dinâmicos.
Ao se projetar sistemas mecânicos e mecatrônicos, além de considerar os graus de liberdade do sistema, temos que considerar o comportamento dinâmico, de forma que o sistema cumpra seus movimentos com os parâmetros adequados de força, torque, velocidade e posição de forma a executá-los de forma rápida e precisa. Vibrações, erros de posicionamento, perda de força com a velocidade entre outros fatores, são parâmetros considerados na engenharia desses sistemas.
Como exemplo de aplicação de um computador analógico eletrônico, vamos exemplificar a simulação de um sistema mecânico representando ¼ de uma suspensão de um carro representado na figura 3.O objetivo é obter a melhor resposta do sistema físico, quando submetido a variações as quais simulam condições de um terreno ou pista.
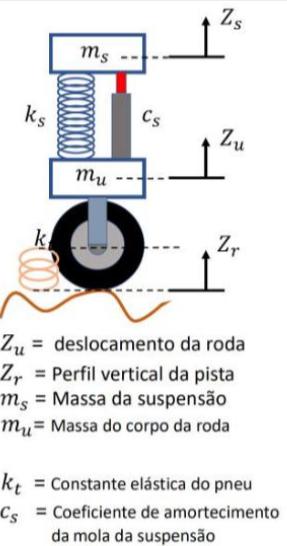
Considerando as melhores condições deste sistema mecânico, devemos evitar oscilações indesejadas ou mesmo ressonância, efeitos que podem tornar instável o funcionamento com consequências catastróficas. De forma oposta, um sistema demasiadamente lento na resposta às variações do terreno poderá ser igualmente prejudicial ao desempenho. Portanto, para que o sistema possa ser projetado de forma satisfatória, um modelo matemático que representa este sistema deve ser elaborado para que, através de simulações, os coeficientes paramétricos possam ser ajustados.
Neste ponto são aplicados métodos computacionais de simulação digitais ou analógicos. No nosso exemplo o sistema será simulado através da computação analógica [8].
Primeiramente o sistema é modelado através de análise dos seus componentes e o comportamento físico de cada um. Em seguida, ao comporem o sistema, os modelos físicos são representados por equações diferenciais, as quais quando submetidas a funções de entrada, respondem com sinais de saída correspondentes. No nosso exemplo, as equações que representam o modelo físico estão na figura abaixo


Partindo destes modelos, podemos montar um sistema de equações as quais serão utilizadas para “programar” nosso computador analógico conforme a figura abaixo.
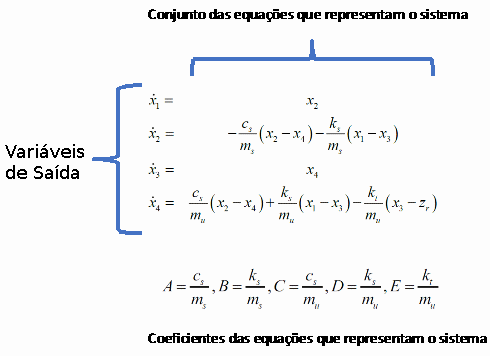
Agora, através dos blocos configuráveis, interligamo-los de forma a representar o conjunto de equações como mostra a figura abaixo.
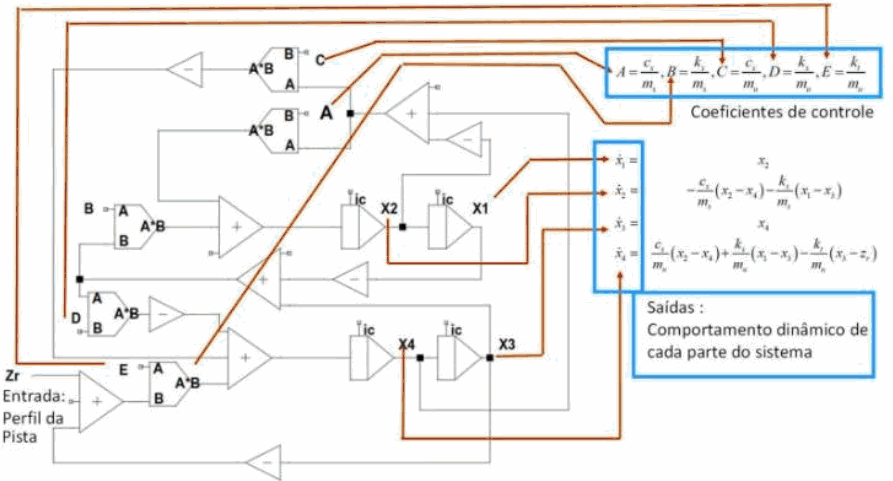
Observando o computador analógico devidamente estruturado, na entrada Zr, submetemos o sistema a oscilações semelhantes às encontradas em uma estrada, uma pista, ou uma estrada de terra etc. Supondo que a suspensão seja submetida a uma variação brusca, através de um impulso tipo degrau, representando por exemplo uma elevação, uma pedra ou um buraco. Para controlar e ajustar os parâmetros do sistema para que a resposta seja a mais rápida e suave possível, alteramos os coeficientes A,B,C,D,E os quais estão relacionados às grandezas físicas envolvidas (Força, Velocidade, Viscosidade, Constantes Elásticas etc..). A resposta a esse degrau poderá ser vista e registrada e os parâmetros serem ajustados por equivalência entre o coeficiente e a tensão, a serem colocados nas entradas.
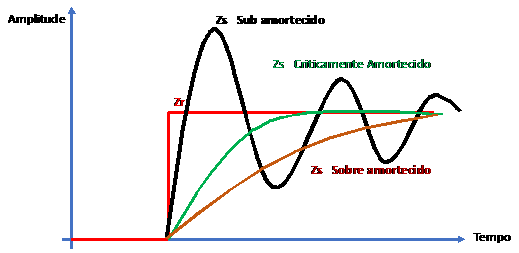
A computação analógica irá simular o sistema mecânico e suas respostas aos impactos simulados, gerando sinais elétricos equivalentes às grandezas. Alterando e ajustando os coeficientes A, B, C, D, E podemos alterar as respostas da simulação até obter os parâmetros de resposta desejado. Como exemplo, o degrau Zr simula um impacto gerado pela estrada ou pista. As respostas mecânicas a este impacto são representadas pelas curvas Zs mostradas na figura 7. Em termos práticos a suspensão pode oscilar de forma sub amortecida gerando instabilidade no veículo ou de forma criticamente amortecida, amortecer o impacto de forma rápida e eficiente ou sobre amortecida onde o impacto é aplicado, mas o sistema é mais lento para recompor-se da excitação em Zr, podendo também instabilizar o veículo. Observe que o computador analógico responde de forma elétrica, gerando sinais que correspondem às grandezas ensaiadas.
5. Fusão entre a computação analógica, processamento de sinais e computação digital
Os computadores atuais, aplicados a sistemas de controle e computação de sinais são baseados em sistemas de alto desempenho com processadores tipo DSP (Digital Signal Processors), os quais são extremamente rápidos e sua arquitetura foi projetada para processamento de sinais em frequências cada vez mais altas. Um dos exemplos atuais são os osciloscópios digitais, os quais tem como base os DSP´s. Ao processar sinais eles precisam converter sinais analógicos em digitais (A/D), através de técnicas as quais preservam as características do sinal analógico após o processo. Uma vez convertidos em dados, o processador aplica os algoritmos matemáticos desejados, obtendo em sua saída o resultado deste processamento armazenando em memória. O passo seguinte é realizar a conversão digital para analógica (D/A) e/ou utilizar os dados digitalizados para operações matemáticas, plotar sinais em displays etc. com precisão. Graças a tais características, os computadores analógicos perderam espaço uma vez que as variáveis analógicas necessitam ser muito bem controladas para obtenção de resultados precisos, além dos enormes benefícios que os DSP´s trouxeram na aplicação de muitos aparelhos e instrumentos eletrônicos. Assim os computadores analógicos ficaram restritos a aplicações científicas específicas em universidades.
Perspectivas da Computação Analógica
Com o avanço tecnológico nas áreas de circuitos analógicos, a viabilidade da composição de sistemas híbridos entre computadores analógicos e digitais, avança, uma vez que a uma boa parte dos problemas dos computadores analógicos referentes ao controle de variáveis e erros estão sendo resolvidos através de integração e novas tecnologias em amplificadores operacionais. Assim, os benefícios da computação analógica ao trabalhar de forma contínua no tempo, complementam as etapas utilizadas pelos sistemas digitais, podendo executar o trabalho de processar sinais que posteriormente serão digitalizados e de forma mais simples processados por DSP´s. Portanto, ao trabalharem em conjunto, a capacidade e desempenho de sistemas híbridos se mostram muito promissores.[9][10]
Referências.
[1] Scheber Bill Analog computation, Part 1: What and why jan 14, 2019 – Article https://www.analogictips.com 28/05/2021
[2] MacLennan Bruce J. A Review of Analog Computing Technical Report UT-CS-07-601 * Department of Electrical Engineering & Computer Science University of Tennessee, Knoxville September 13, 2007
[3] Köppel S. Ulmann B, Heimann L. Killat D, About using analog computers in today’s largest computational challenges GmbH, Am Stadtpark 3, 12167 Berlin, Germany Microelectronics Department, Brandenburg University of Technology
[4] https://www.newtoncbraga.com.br/index.php/computacao-analogica/16420-computacao-analogica-licao-1-os-computadores-analogicos-cur6001.html - 28/05/2021
[6] AD 633 Low-Cost Analog Multiplier Analog Devices datasheet Analog Devices, Inc., 2002
[7] Kluever, Craig A. Sistemas dinâmicos: Modelagem, simulação e controle. São Paulo: LTC, 2017.
[8] Introduction to analog computing - Article https://www.elettroamici.org/en/ 31/05/2021
[9] Huang, Yipeng Hybrid Analog-Digital Co-Processing for Scientific Computation –Rutgers University 08/05/2021
[10] Crane, L Back to analog computing: merging analog and digital computing on a single chip Article COLUMBIA UNIVERSITY IN THE CITY OF NEW YORK Electrical Engineering December 04, 2016
Rev4



















