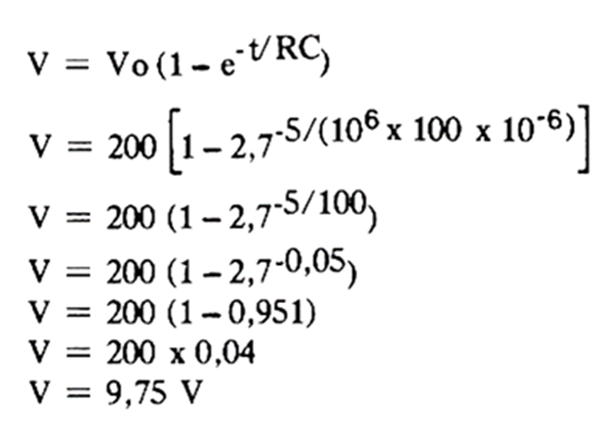O que é constante de tempo? O que acontece com um capacitor e um resistor, quando são ligados em série, por exemplo? Os leitores certamente já ouviram falar muitas vezes dos denominados circuitos RC, mas será que sabem exatamente como funcionam? Neste artigo teórico faremos algumas considerações importantes sobre estes circuitos que certamente ajudarão os leitores a fazer seus próprios projetos que envolvam constante de tempo.
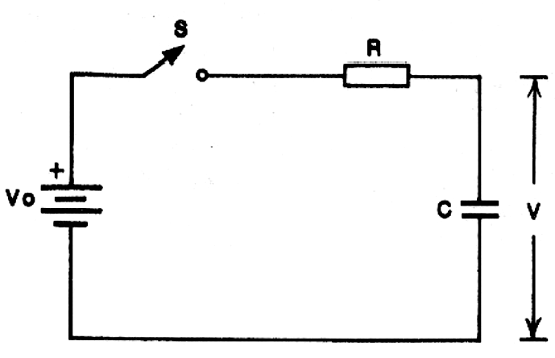
Podemos partir em nossas considerações de um circuito muito simples, que é mostrado na figura 1.
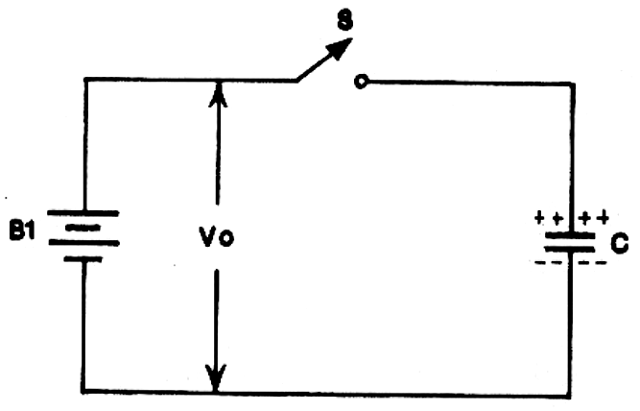
Neste circuito temos um gerador (bateria) ideal, um interruptor (também ideal) e um capacitor (ideal). Lembramos apenas que o capacitor ideal não deve ter resistência alguma de terminais e isolamento infinito, ao mesmo tempo em que o interruptor com estas características deve ter resistência nula quando fechado. Já a bateria ideal deve ter resistência interna nula, o que significa uma capacidade ilimitada de fornecimento de corrente.
É claro que na prática tais dispositivos não existem, mas servem como exemplo para nossas explicações, para facilitar a compreensão dos fenômenos que queremos descrever.
Nas condições indicadas, supondo que o capacitor esteja completamente descarregado, quando a tensão entre as suas armaduras é nula, ligamos o interruptor estabelecendo uma corrente de carga.
Como a resistência interna do gerador é nula e a resistência do interruptor é nula também, a carga será praticamente instantânea, atingindo logo as armaduras a tensão do gerador, conforme ilustra o gráfico da figura 2.
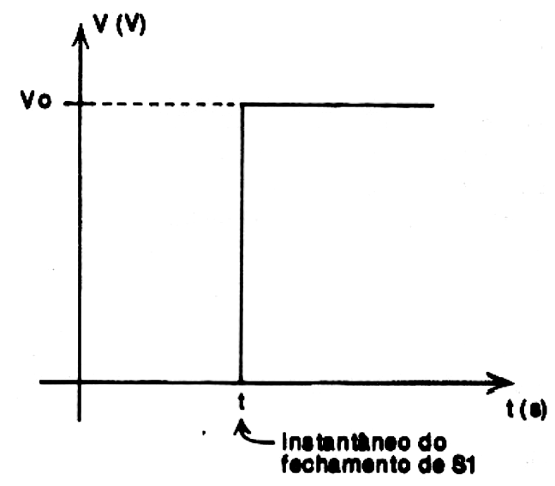
É claro que na prática esta carga não é instantânea. Resistências diversas associadas ao gerador, ao interruptor e ao próprio capacitor tornam a carga mais lenta, mas, mesmo assim relativamente rápida.
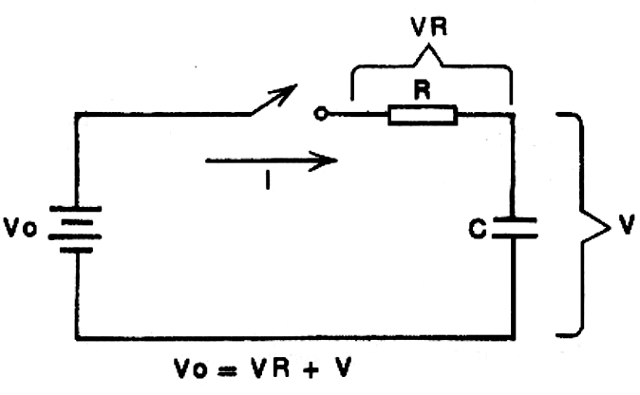
Se fosse ligada em série com o capacitor uma resistência de valor que não pudesse ser desprezado, o que aconteceria ao ligarmos o interruptor? Partindo então do circuito da figura 3, vamos tentar explicar o que aconteceria a partir do momento em que o interruptor fosse fechado.
Na condição de completamente descarregado, a tensão nas armaduras do capacitor é nula.
No instante em que ligarmos o interruptor, estabelecendo uma corrente de carga, esta começa a fluir para as armaduras do capacitor, elevando assim seu potencial gradualmente, no sentido de alcançar um equilíbrio. Neste ponto a tensão entre as armaduras deveria ser teoricamente igual à existente entre os polos do gerador.
O comportamento desta corrente, entretanto, deve ser analisado com cuidado.
De início, quando completamente descarregado, o capacitor "aceita" com facilidade a carga, pois a diferença de potencial existente entre o gerador e o capacitor é a maior possível (o gerador com + V e o capacitor a zero). Mas, à medida que o capacitor se carrega, a tensão nas suas armaduras vai subindo, de modo que se reduz a diferença de potencial que "empurra" mais carga.
Em suma, a carga não se faz com uma corrente constante, mas sim com uma corrente que vai reduzindo de valor gradualmente.
Quanto mais nos aproximamos da carga total, menor se torna a diferença de potencial que "empurra" mais cargas, e, portanto, mais difícil se torna a chegar a este ponto.
Temos então uma curva que é mostrada na figura 4.
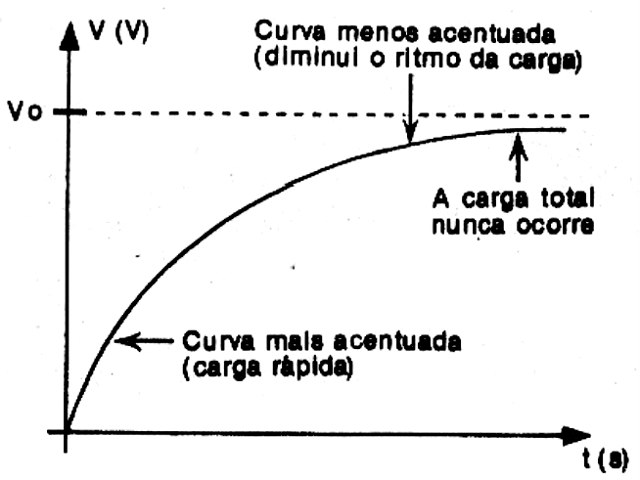
De início a corrente é maior e a tensão nas armaduras do capacitor sobe rapidamente. Mas, à medida que alcançamos pontos de maior carga, a corrente se reduz e qualquer crescimento posterior da tensão torna-se mais lento (menos acentuado pela curva).
Veja que a curva nunca atinge o ponto máximo, que corresponde à carga total do capacitor, mas sim tende a ele. O capacitor, por mais que tentemos carregá-lo, nunca chegará a uma carga que permita obter entre suas armaduras a tensão do gerador.
No gráfico que representa esta carga existe um ponto muito importante que nos chama a atenção. Trata-se do ponto em que é atingido 63,2% da carga máxima do capacitor ou 63,2% da tensão do gerador (fig.5).
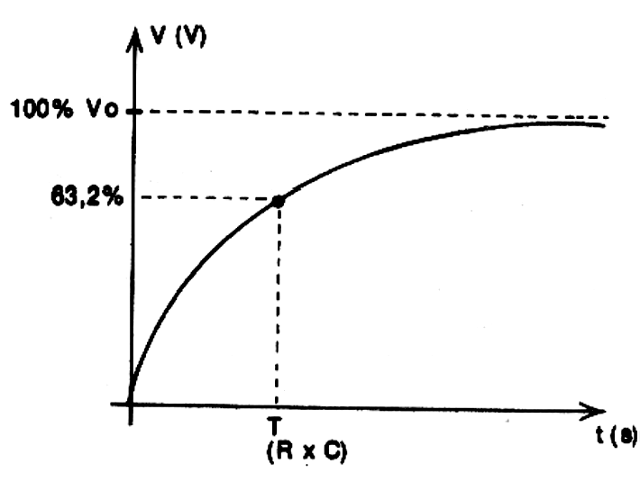
O tempo em que o capacitor chega a esta carga corresponde numericamente ao produto de seu valor (em farads) pela resistência ligada em série.
Supondo que T seja o tempo que ocorre desde o instante em que estabelecemos a tensão no circuito, que R seja a resistência em ohms ligada em série, e que C seja a capacitância do capacitor em farads, podemos escrever.
T= R x C
Este "tempo" é uma constante, pois independe da tensão de alimentação. Qualquer que seja a tensão aplicada no circuito RC, aquela porcentagem de 63,2% será atingida decorrido o mesmo intervalo.
Denominamos então este "T" de constante de tempo do circuito RC, ou simplesmente constante de tempo RC.
Do mesmo modo que obtemos uma constante RC para a carga do capacitor, também temos uma constante para a descarga, conforme o circuito mostrado na figura 6.
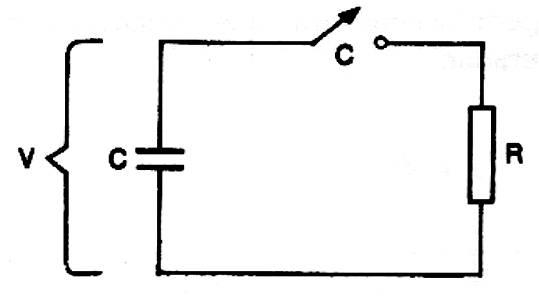
Se um capacitor carregado totalmente, de modo a manter entre suas armaduras uma certa tensão V, for ligado a um resistor, conforme mostra a figura 7, a descarga também não será constante, ou seja, com uma corrente sempre de mesma intensidade.
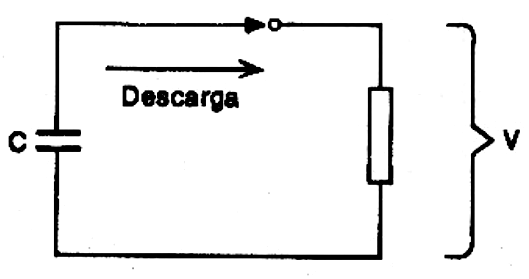
Inicialmente a corrente fluirá com maior intensidade, pois teremos uma tensão maior para "empurrá-la" através do resistor. Mas, à medida que a descarga for ocorrendo, a tensão irá caindo nas armaduras do capacitor de modo que a "causa" para a circulação da corrente também será menor. A medida que a tensão nas armaduras cai, a corrente também reduz sua intensidade, reduzindo o "ritmo' da descarga. Obtemos então uma curva de descarga conforme mostra a figura 8.
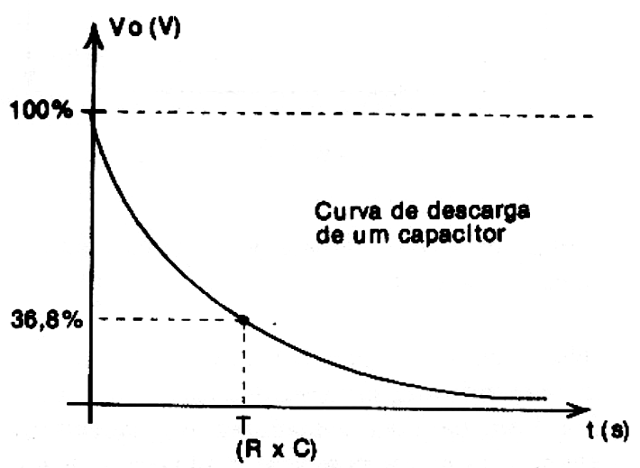
Do mesmo modo que no caso da carga, a curva também tangencia no infinito a reta que corresponde à descarga completa. Isso quer R dizer que, na teoria, a descarga completa nunca ocorre.
Neste gráfico temos um ponto igualmente importante, que corresponde a 36,8% da tensão inicial. Este ponto corresponde ao tempo que obtemos multiplicando numericamente o valor do capacitor em farads pelo valor do resistor em ohms.
Temos então a constante de tempo RC do circuito de descarga dada pela fórmula:
T= R x C
Nas aplicações práticas é importante o conhecimento da constante de tempo de um circuito, pois ela está relacionada com a sua frequência de operação, como por exemplo no multivibrador da figura 9.
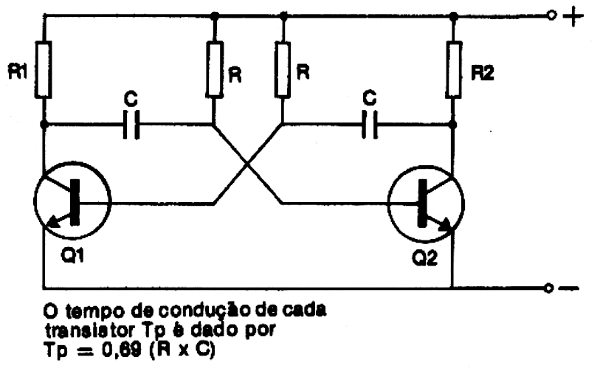
Entretanto, em alguns casos não é propriamente a constante de tempo que nos dá a frequência, mas sim valores que não correspondem propriamente à carga indicada.
Assim, num oscilador como o 555, conforme a figura 10, o disparo ocorre com 2/3 e 1/3 da tensão do capacitor, conforme mostram as curvas associadas, o que nos leva a valores diferentes das constantes de tempo.
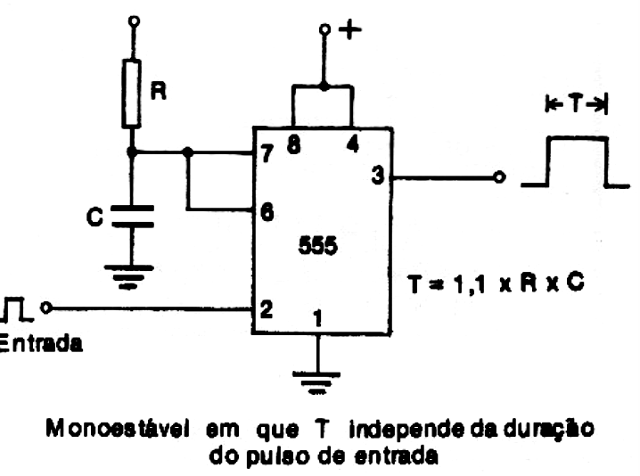
Na verdade, 2/3 correspondem a 66,6% da carga do capacitor, um valor um pouco maior que 63,2% da constante RC. Daí o tempo de um monoestável como o 555 ser dado não por RC, mas sim por 1,1 x R x C.
Para calcular a tensão atingida no capacitor em cada instante devemos partir para uma fórmula mais complexa.
De fato, como a causa da corrente, que é diretamente proporcional à tensão, depende também do fator tempo, uma fórmula que nos dê a tensão em cada instante deve obrigatoriamente ser uma função exponencial do tempo.
Podemos deduzir a fórmula da seguinte maneira:
Partindo da carga de um capacitor em função de sua capacitância e tensão, escrevemos:
Q = V x C
Diferenciando cada membro desta equação, temos:
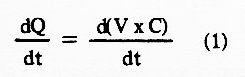
Mas, sendo C constante temos que dC /dt = O.
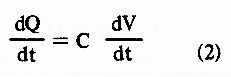
A relação dQ/dt nada mais é do que a corrente que flui no circuito 1. Podemos então escrever:
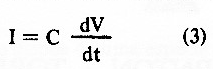
Pelo circuito, vemos que a tensão no resistor VR é dada por Vo - V, e segundo a Lei de Ohm (fig.11):
(Vo - V)/R = I
Substituindo em (3):
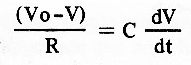
Passando R para o segundo membro:
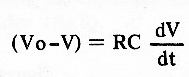
Resolvendo matematicamente esta equação V = 200 (1 - 2,7-0,05) diferencial, obtemos:
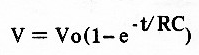
onde e é uma constante que vale 2,7182818. Este valor pode ser aproximado para 2,7 nos cálculos mais simples.
Um exemplo de como usar esta fórmula:
Ex: Qual é a tensão num capacitor de 100 µF em série com um resistor de 1 M ohm ligados a um gerador de 200 V depois de 5 segundos?
Neste caso temos:
R = 106 ohms
C = 100 x 10-6 farads
Vo = 200 volts
s = 5 segundos