A maioria dos circuitos eletrônicos trabalha com sinais que correspondem a correntes alternadas de diversas frequenc1as. Por um sinal entendemos uma corrente que varie periodicamente de intensidade mudando, por exemplo, de polaridade em intervalos regulares.
Se abrirmos e fecharmos um interruptor rapidamente, de modo a termos tensões produzidas em intervalos regulares num circuito de carga, conforme ilustra a figura 1, estaremos gerando um sinal.
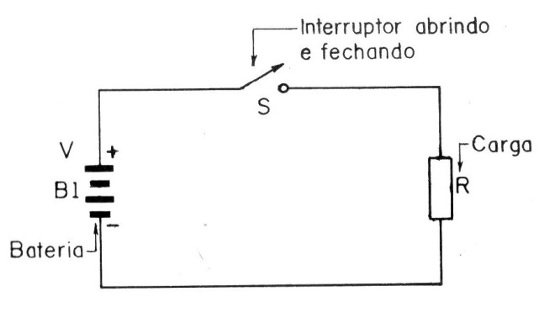
As características de um sinal podem ser dadas de diversas formas:
a) A frequência, que é o número de vezes em cada segundo em que os valores de tensão ou corrente se repetem. No caso da chave tomada como exemplo, a frequência será dada pelo número de vezes em cada segundo que a fechamos (ou abrimos).
b) A forma de onda que é mais importante, no nosso caso, pois diz de que modo a corrente ou a tensão variam num determinado intervalo de tempo considerado.
Para entender melhor o que vem a ser a forma de onda, será interessante também definirmos o que vem a ser período e um ciclo do sinal.
No caso de um interruptor que abre e fecha, se partimos do instante inicial em que ele está aberto, e depois o fecharmos, quando o abrirmos novamente teremos completado um c1clo de sua operação.
Fechando novamente este interruptor o ciclo se repete e assim indefinidamente enquanto atuarmos sobre ele.
Representando por um gráfico o que ocorre com a tensão aplicada no circuito de carga formado por um resistor R, vemos que num ciclo temos duas situações:
Fase inicial em que a tensão na carga é nula.
Fase final em que a tensão é máxima.
A subida da tensão na carga de zero para o valor máximo pode ser considerada instantânea. Veja a figura 2.
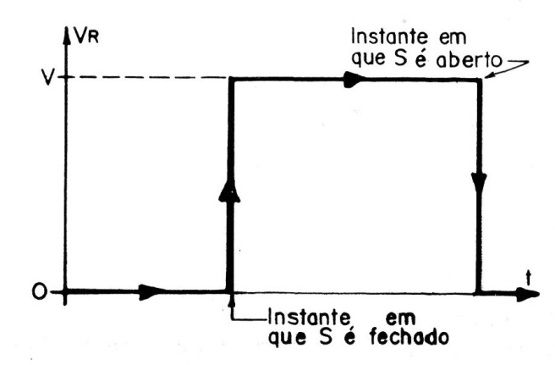
Observando a figura que o gráfico forma vemos que ela se assemelha ao degrau de uma escada com uma transição rápida de o até o máximo.
Se representarmos diversos ciclos em seguida, conforme mostra a figura 3, teremos um “retrato” desta forma de onda peculiar que representa variações rápidas da corrente ou tensão em R.
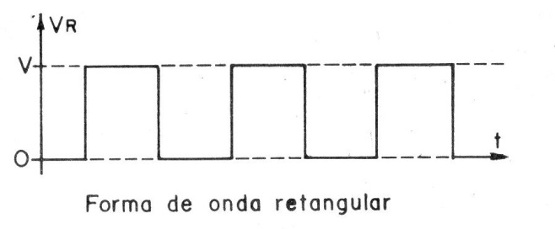
Esta forma de onda é denominada “retangular", pois os ciclos têm este formato geométrico na sua representação.
E interessante observar que a corrente que corresponde a um sinal deste tipo fisicamente não tem nada de retangular, pois nem sequer tem forma definida. Trata-se de um fluxo de elétrons que não tem massa perceptível e nem pode ser visto, daí não poder ser definida a forma.
O nome dado a este tipo de corrente que tem variações bruscas vem da sua representação gráfica que, conforme vimos, é correspondente a retângulos.
Na figura 4 temos um tipo de forma em que os intervalos são maiores que os pulsos em sua duração.
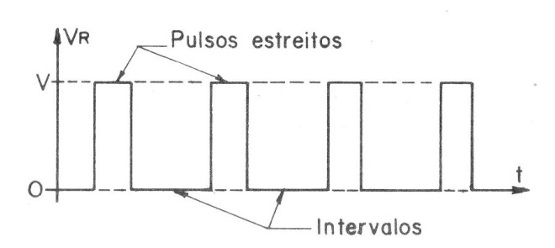
Esta também é uma forma de onda retangular.
Vamos supor agora um outro tipo de corrente que também corresponde a um sinal.
Imaginemos uma espira de fio condutor que corta num movimento circular as linhas de força de um campo magnético, conforme mostra a figura 5.
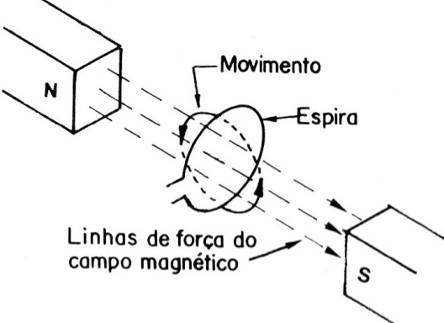
O que temos nesta estrutura é um gerador de corrente alternada que gera um tipo de sinal muito especial. Quando a espira gira e entra no campo magnético, cortando as linhas de força, é induzida uma tensão que cresce suavemente de valor até atingir o máximo a 1/4 da volta completa.
A partir deste ponto, a tensão gerada em suavemente até atingir novamente o ponto mínimo (zero) em 1/2 volta.
Continuando com o movimento, a tensão novamente aumenta suavemente de valor, mas como o movimento agora corta as linhas de força no sentido contrário, a tensão é negativa. A 3/4 de volta a tensão negativa atinge seu ponto máximo, para cair novamente a zero na volta completa.
Se representarmos a tensão gerada por este movimento da espira num gráfico, teremos uma curva suave, conforme mostra a figura 6.
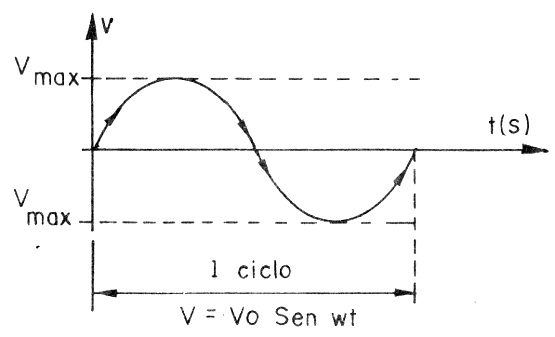
Esta curva pode ser expressa por uma função matemática denominada senóide que atribui um valor a cada ângulo da volta. Dizemos então que a forma de onda desta corrente é senoidal.
A corrente alternada que obtemos na tomada de força de nossas casas tem forma de onda senoidal, pois os geradores que as produzem operam segundo o mesmo princípio da espira que tomamos como exemplo.
É claro que a corrente em sí, nada tem de senoidal, pois ela não pode ser vista, mas sua representação leva a uma figura que é uma senóide, daí dizermos que a forma de onda corresponde à senóide.
A frequência da corrente alternada da rede é 60 hertz (60 ciclos em cada segundo) mas os circuitos eletrônicos trabalham com frequências de sinais senoidais que podem chegar a centenas de milhões de hertz.
Para gerar formas de ondas senoidais ou retangulares não precisamos ter obrigatoriamente chaves ou espirais cortando campos magnéticos. Circu1tos eletrônicos podem fazê-lo com facilidade.
Finalmente, temos uma terceira forma de onda que corresponde a variações de tensão que sobem e descem linearmente, conforme mostra a representação gráfica da figura 7.
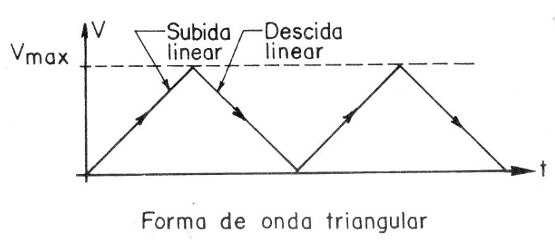
Esta forma de onda é denominada triangular, também pelo fato de sua representação lembrar a superposição de triângulos de diversos tipos.
Quando aplicamos sinais de formas de ondas diferentes nos circuitos, dependendo de sua natureza eles não reagem do mesmo modo. Cada tipo de sinal tem suas características próprias em relação a um circuito, o que faz com que devamos escolher de modo apropriado qual usar, quando utilizarmos, por exemplo, um gerador de funções.
O que caracteriza cada tipo de sinal será visto a seguir:
Sinal senoidal
O sinal senoidal corresponde a uma oscilação pura, ou seja, uma oscilação que ocorre naturalmente. Se fizermos um corpo vibrar, um pêndulo balançar ou um circuito eletrônico formado por uma bobina e um capacitor entrar em oscilação, a representação desta oscilação será um senóide, conforme a figura 8.
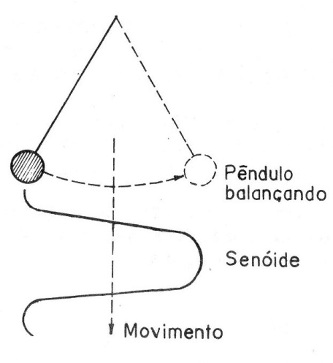
A senóide corresponde ao tipo de oscilação que ocorre da maneira mais suave possível, ou seja, àquela que tende a ocorrer naturalmente. Os sons puros, têm formas de ondas senoidais como, por exemplo, o produzido por um diapasão, usado na afinação de instrumentos.
Na figura 9 damos um exemplo de circuito eletrônico que pode produzir um sinal senoidal.
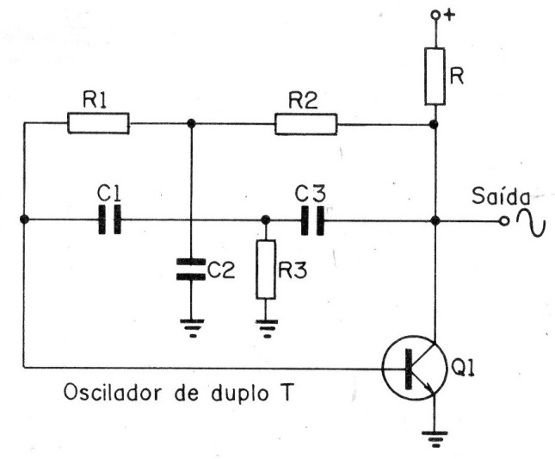
Uma característica importante de um sinal senoidal puro é que ele está presente numa única frequência, ou seja, na forma fundamental.
O que ocorre é que, quando um sinal não puro é produzido, frequências de valores múltiplos também aparecem, conforme ilustra a figura 10.
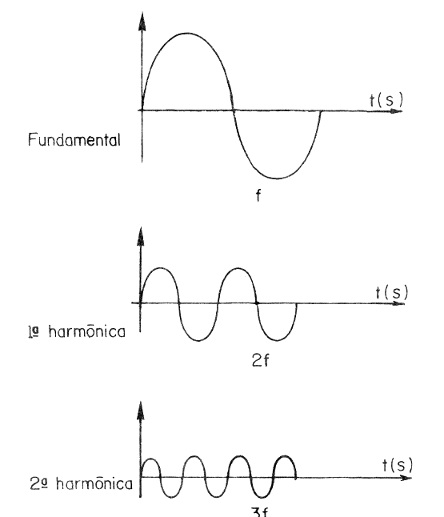
Estas frequências são denominadas “harmônicas” e correspondem ao dobro, ao triplo, ao quádruplo da frequência fundamental.
Quando queremos trabalhar com filtros, circuitos que devam operar numa única frequência, a forma de onda utilizada é a senoidal.
Assim, na prova de circuitos deste tipo devemos usar sinais senoidais, o mesmo ocorrendo com um amplificador quando quisermos verificar sua reprodução de um sinal de uma única frequência.
Sinal retangular
Segundo Fourier, podemos produzir qualquer tipo de sinal a partir da combinação em proporções adequadas de sinais senoidais e suas harmônicas.
Assim, um sinal retangular pode ser conseguido pela superposição de um sinal senoidal com diversas de suas harmônicas, conforme sugere a figura 11.
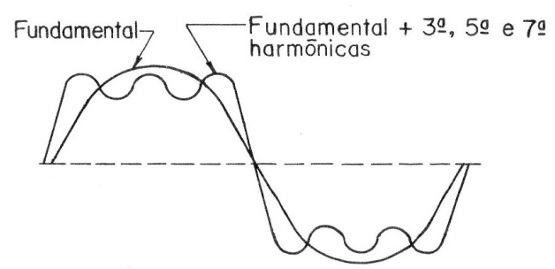
Tanto isso é válido que a recíproca é verdadeira: um sinal retangular possui grande quantidade de harmônicas que se estendem em uma faixa infinita de valores.
Assim, um sinal retangular não é puro, mas composto de uma grande quantidade de harmônicas que cobrem um espectro relativamente amplo. Intensidade relativa
Na prática, por exemplo, gerando um sinal retangular de 1 kHz podemos ter tantas harmônicas que sua presença se fará sensível mesmo em frequências tão altas como 10 ou 20 MHz.
Na figura 12 temos uma ideia do espectro coberto por um sinal retangular de 1 kHz.
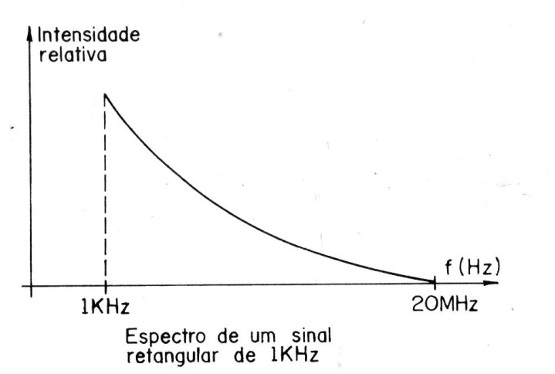
Esta grande quantidade de harmônicas é que faz com que os circuitos de injetores de sinais operem com formas de ondas retangulares preferivelmente.
Na figura 13 temos um circuito de injetor de sinais bastante simples que o leitor pode montar para suas provas de bancada.
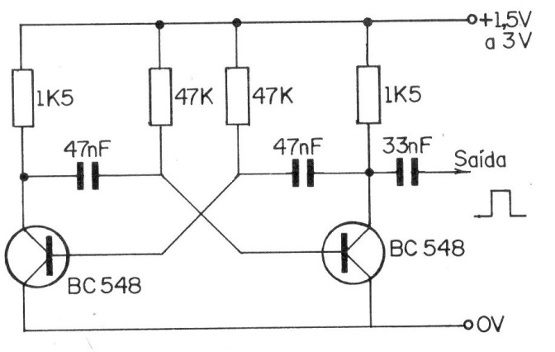
Os transistores são de uso geral (BC548 ou equivalentes) e os resistores são de 1/8 ou 1/4 de watts, conforme sua disponibilidade.
Os capacitores determinam a frequência fundamental do sinal produzido que pode estar em torno de 1 kHz para maioria das aplicações práticas.
Instalado num tubo de PVC e alimentado por uma única pilha este circuito serve não só para provas em circuitos de áudio (quando se aproveita a frequência fundamental) como também para provas em circuitos de RF quando se aproveitam as frequências harmônicas, veja a figura 14.
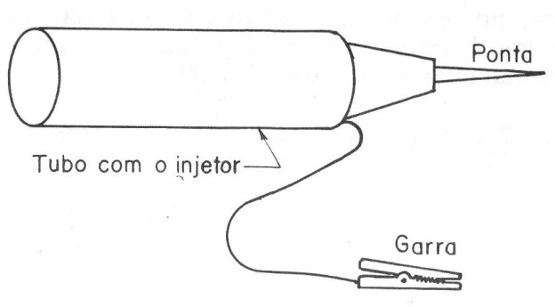
O nosso gerador de sinais pode ser usado na forma de onda retangular com a mesma finalidade que um injetor.
Usaremos esta forma de onda para excitar circuitos de RF, com frequências bem acima dos limites previstos para o oscilador. A presença de grande quantidade de harmônicas permite que até circuitos de FM seja analisados com o gerador que fundamentalmente opere numa faixa de áudio.
Para usar o gerador como injetor, é bastante simples: basta aplicar o sinal na entrada da etapa que se deseja analisar, sempre lembrando que a intensidade do sinal para as harmônicas decai à medida que sua frequência aumenta. Assim, se temos alguns volts no fundamental, nas harmônicas os sinais podem ter apenas alguns milivolts ou mesmo microvolts.
Outra aplicação para os sinais retangulares é na prova de circuitos lógicos digitais.
Estes circuitos operam com dois níveis de tensão 0 e 5 V para os TTL e , O e Vcc onde Vcc é a tensão de alimentação, para os CMOS.
A velocidade de operação destes circuitos pode superar os 10 MHz, o que implica na produção ou recepção de sinais retangulares destas frequências.
Um gerador de sinais retangulares pode, pois, ser usado para provar estes circuitos.
Entretanto, para a utilização de um gerador nestas condições é preciso que o nível de sinal de saída seja perfeitamente conhecido.
Se o sinal estiver abaixo de certo limite de valor, não haverá excitação do circuito em prova e se for superior a tensão de alimentação corre-se o risco de danificar o circuito em prova.
A utilização de um sinal retangular na prova de amplificadores de. áudio e. circuitos semelhantes,.exige a presença de um osciloscópio.
Deformações na forma de onda, como as mostradas na figura 15 indicam diversos tipos de problemas.
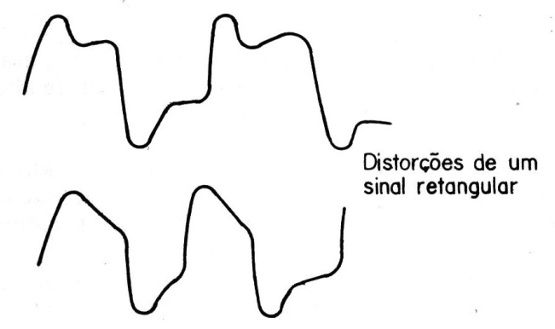
A ligação do gerador e do osciloscópio é feita como mostra a figura 16.
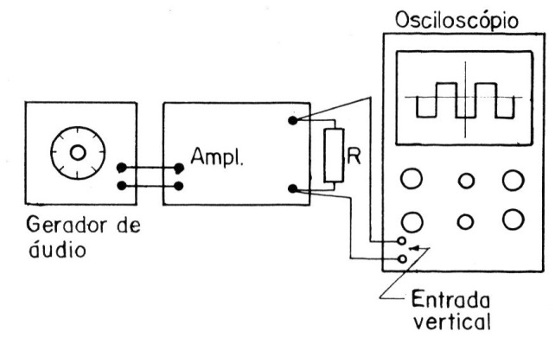
Observe que a carga do amplificador deve ser puramente resistiva sendo então o alto-falante trocado por um resistor de alta dissipação (de acordo com a potência do amplificador).
O nível de sinal de excitação deve ser ajustado de modo a ter excitação à plena potência. Excesso de sinal de excitação também pode provocar distorções que serão verificadas no osciloscópio.
É importante observar que o sinal retangular gerado por um aparelho já pode ser dotado de certa taxa de distorção que deve ser previamente verificada.
Sinais triangulares
Até há, algum tempo atrás havia muita controvérsia quanto ao uso de sinais triangulares em diversos tipos de provas de equipamentos eletrônicos. Tanto é assim, que instrumentos de excelente qualidade de algum tempo atrás não dispunham de sinais com esta forma de onda.
Na figura 17 temos um exemplo de sinal triangular gerado por um instrumento de prova comum.
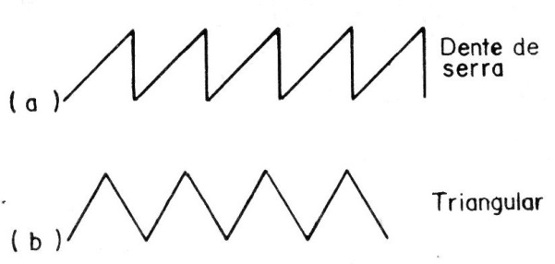
Novamente notamos que a forma triangular refere-se à representação gráfica das variações, nada tendo a ver com o sinal em si.
Um dos argumentos a favor da utilização de sinais triangulares na prova de equipamentos de áudio refere-se à maior facilidade com que podem ser detectadas as distorções.
Enquanto que, com um sinal senoidal, só se pode perceber uma distorção num osciloscópio de pelo menos 5%, utilizando um sinal triangular, qualquer distorção em torno de 2% já pode ser percebida.
Isso significa que, se você provar um amplificador que apresente uma distorção, digamos de 3%, usando sinal senoidal e o osciloscópio, você não vai perceber nada. No entanto, provando o mesmo amplificador com sinal triangular, esta distorção já será facilmente verificada.
Outro fator que aparece a favor da utilização deste tipo de sinal é que as mudanças de traçado de uma forma de onda senoidal, verificadas num osciloscópio são de difícil interpretação.
Temos que analisar uma distorção de função que segue lei trigonométrica, o que não ocorre com o sinal triangular em que os trechos são funções mais simples, segundo leis lineares, conforme a figura 18.
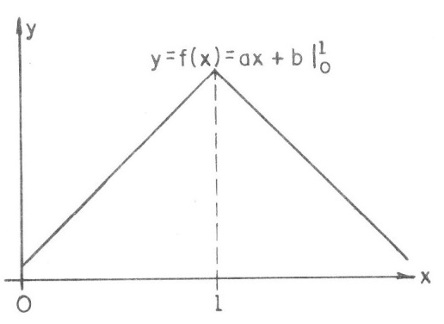
A produção de um sinal triangular é relativamente simples a partir de um sinal retangular. O que se faz é usar um integrador, um circuito RC, conforme mostra a figura 19.
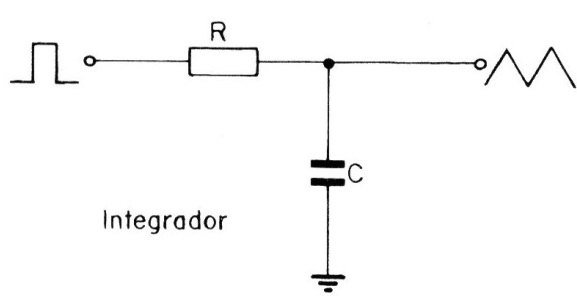
Os valores de R e C são calculados para resultar nos trechos lineares da forma triangular de saída, nas frequências de operação do circuito.
Um integrador mais complexo, usando amplificador operacional é mostrado na figura 20.
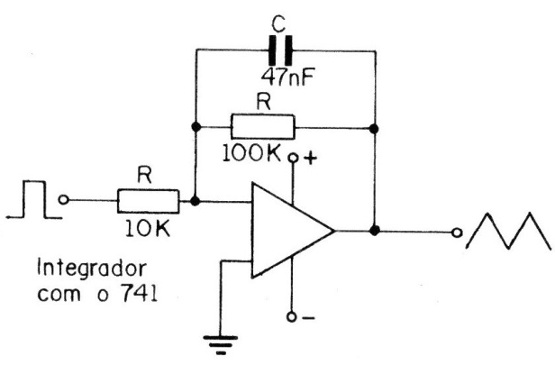
Enfim, os sinais triangulares podem ser usados com as mesmas finalidades dos demais, observando-se que também são ricos em harmônicas que se estendem até as faixas de RF.


















