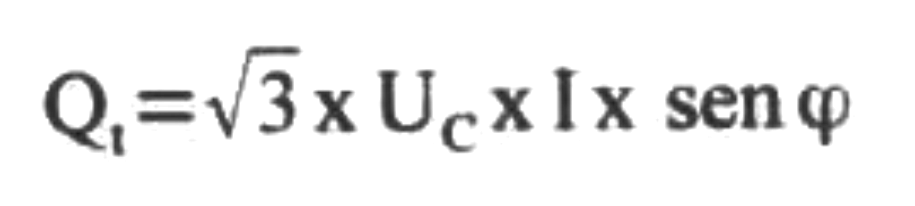A maior parte dos aparelhos eletrodomésticos e industriais de pequena potência são alimentados com tensão monofásica; pelo contrário os aparelhos de maior potência são alimentados com tensão trifásica, porque este sistema oferece as seguintes vantagens:
Nota: Artigo publicado na revista Eletrônica Total 155 de 2013
• Ao nível da produção um alternador trifásico é muito menos volumoso, com melhor funcionamento e mais econômico que um monofásico da mesma potência. Com efeito um gerador trifásico tem uma potência superior de aproximadamente 50%, relativamente à de um alternador monofásico do mesmo volume;
• Ao nível do transporte, se a secção dos cabos fosse feita em monofásico, seria duas vezes superior à secção dos cabos no transporte em trifásico;
• Ao nível da utilização uma linha trifásica oferece aos usuários duas tensões diferentes, tanto a monofásica como a trifásica. Para além disso, os motores assíncronos trifásicos são os mais utilizados na indústria.
Obtenção das tensões trifásicas
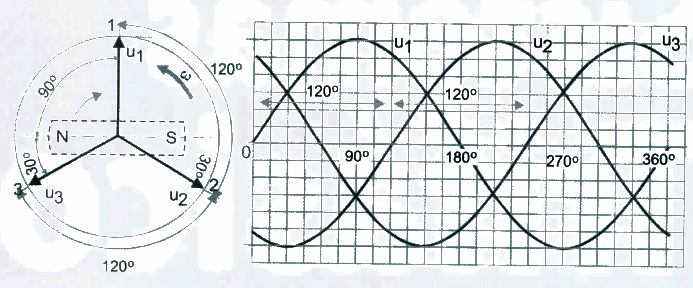
A figura 1 representa um alternador trifásico, a sua construção é idêntica à do alternador monofásico, mas o estator tem três enrolamentos ou fases, todos com a mesma quantidade de espiras.
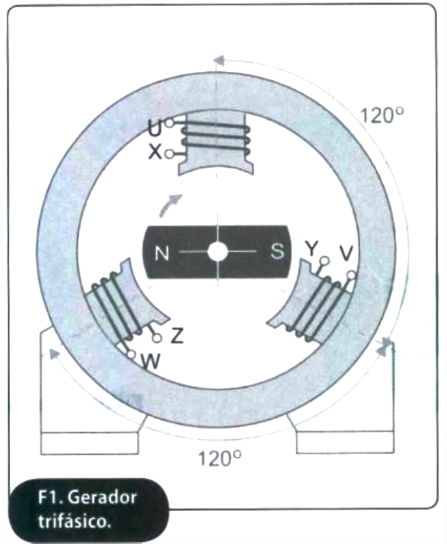
Os eixos destes enrolamentos fazem entre si ângulos de 120°, isto quer dizer que estão deslocados no estator de um terço de circunferência interior.
Como se sabe da indução eletromagnética, sempre que um condutor fica sujeito a um campo magnético variável, induz-se nele um f.e.m.; assim, ao rodar o ímã segundo um eixo perpendicular ao seu plano, constituindo o indutor ou rotor, haverá um campo magnético variável e nos condutores dos enrolamentos uma f.e.m. induzida. O ímã permanente rodando a uma velocidade constante, produzirá três f.e.m. desfasadas entre si de 120°. Com efeito quando se verifica a indução máxima num enrolamento, só passado algum tempo é que o enrolamento seguinte toma o mesmo valor, querendo isto dizer que em cada 120' rodados, temos uma f.e.m. no valor máximo.
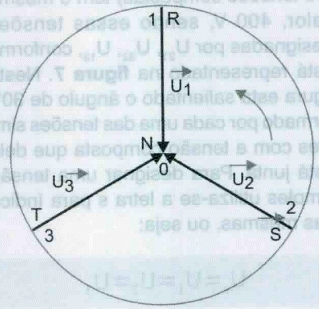
Estas f.e.m. originam três tensões simultâneas nos terminais dos enrolamentos, que podem ser representadas num sistema de eixos cartesianos, marcando-se nas ordenadas os valores das tensões obtidas em cada par de terminais e nas abcissas os ângulos descritos pelo ímã ou o tempo gasto. Para a posição do ímã, figura 2, a tensão U1 está passando pelo zero, U2 está aumentando, atingindo o valor máximo negativo com mais de 30°, e U3 está diminuindo, anulando-se quando o ímã rodar 60°.
O mesmo sistema trifásico pode ser representado vetorialmente através de três vetores girantes que façam entre si um ângulo de 120°, a amplitude de cada vetor corresponde ao valor eficaz da grandeza considerada. A ordem de sucessão das fases 1-2-3, diz-nos que vai aparecer em primeiro lugar a fase U1, em seguida U2 e por último U3.
Podemos considerar cada enrolamento como gerador de uma tensão monofásica e, como temos três enrolamentos, obtemos um sistema trifásico. Um sistema trifásico de tensões é constituído por três tensões monofásicas desfasadas entre si de 120°.
Ligações trifásicas de receptores
Certos receptores apresentam dois terminais de ligação (lâmpadas, aquecedores, etc.), sendo por isso denominados receptores ou cargas monofásicas. O agrupamento de três receptores monofásicos ligados por um sistema de tensões trifásicos, constitui um receptor trifásico. A ligação dos três receptores monofásicos para dar um trifásico pode ser feita de duas formas diferentes:
• Ligação em estrela;
• Ligação em triângulo.
Ligação em estrela
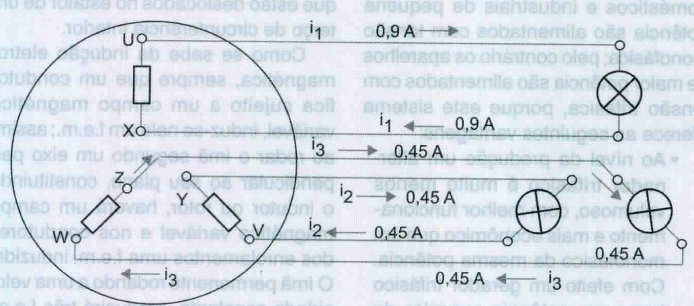
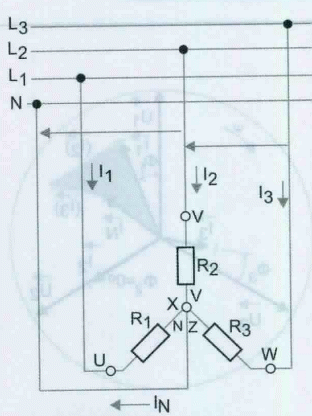
Consideremos três lâmpadas iguais ligadas aos enrolamentos do gerador, por condutores de cobre iguais, designando os terminais de cada um dos enrolamentos por UX,VY e WZ, como se indica na figura 3.
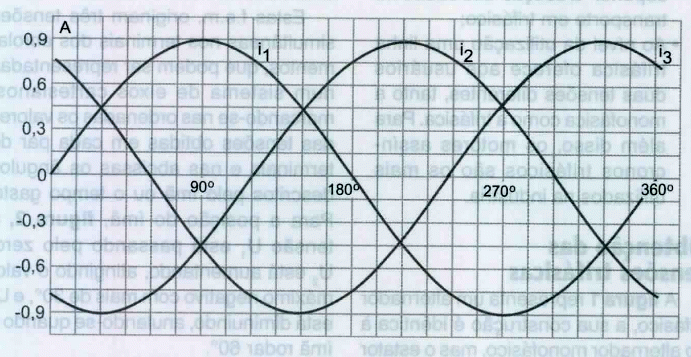
Devido às cargas nos três circuitos serem iguais, temos três intensidades de corrente com formas análogas à das tensões, isto é, com períodos iguais, valores máximos iguais e desfasadas de 120°, figura 4.
No instante correspondente aos 90°, a intensidade de corrente que atravessa o circuito 1, i1, atinge o seu valor máximo positivo de 0,9 A, e os valores das intensidades de corrente nos circuitos 2 e 3, i2 e i3, no instante considerado, são de -0,45 A.
Ao atingir os 120° a intensidade de corrente no circuito 2 é nula (i2 = 0), e as intensidades de corrente nos circuitos 2 e 3(i2 e i3) são iguais mas de sentidos contrários, sendo a sua soma nula (i2 - i3 =0).
Os três condutores ligados aos terminais X, Y, Z dos enrolamentos são percorridos em qualquer instante por valores de intensidade de corrente, cuja soma algébrica é nula, portanto se substituirmos esses três condutores por um único, nele não passará corrente (figura 5).
Passamos assim de seis condutores para quatro, podendo ainda ser reduzido para três, visto que, no condutor central não passa corrente. De fato, quando as cargas nas fases estão equilibradas, a soma algébrica das intensidades de corrente que passam nos condutores ligados a X, Y e Z é nula e, se isto não acontecer, então no condutor central passará uma intensidade de corrente. Este condutor é designado por condutor de neutro e, em geral, está ligado à terra nos postos de transformação ou na central. O ponto de reunião das três fases é denominado ponto neutro. Como os três receptores estão ligados a um ponto comum, designa-se esta ligação como ligação em estrela.
Relação entre tensões
Medindo a tensão entre o neutro e qualquer dos condutores das fases, obtemos três valores iguais de 230 V.
U1 =U2= U3=230 V
Esta tensão obtida entre qualquer condutor de fase e o neutro, é designada por tensão de fase ou tensão simples. Em qualquer instante a soma vetorial das três tensões é nula, U1 + U2 + U3 = 0, como se pode verificar no diagrama vetorial da figura 6, mas a soma algébrica é diferente de zero, ou seja, a soma vetorial de U1, U2 e U3 é igual a zero, porém a soma algébrica é diferente de zero.
Já medimos as tensões entre o neutro e cada uma das fases, podemos verificar o que acontece ao medir as tensões entre cada uma das fases. Na nossa rede as três tensões entre fases (ou tensões compostas) têm o mesmo valor, 400 V. sendo essas tensões designadas por U21, U32, U13, conforme está representado na figura 7. Nesta figura está salientado o ângulo de 30", formado por cada uma das tensões simples com a tensão composta que dela está junta. Para designar uma tensão simples utiliza-se a letra s para índice das mesmas, ou seja, Us é igual a U1, que é igual a U2 e que é igual a U3.
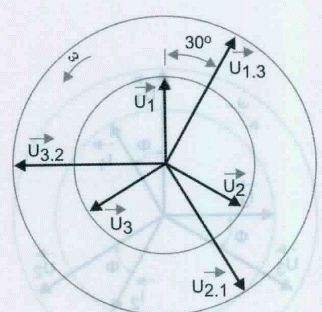
Para designar a tensão composta utiliza-se a letra c, ou seja:
Uc = U21 = U32 = U13
Para saber qual a relação que existe entre os valores da tensão simples e da tensão composta, temos que analisar a figura 8.
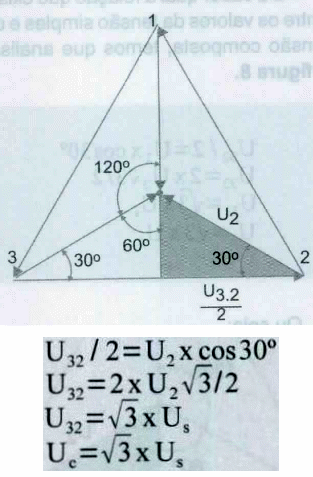
Ou seja:
400 / 230 = Raiz(3)
Relação entre correntes
Atente para a figura 9. Consideremos um receptor trifásico montado em estrela e ligado à rede (figura 9), neste tipo de montagem a tensão a que está submetido cada receptor é a tensão simples, 230 V. entre a fase e o neutro. Por outro lado, a intensidade de corrente em cada fase I, é a mesma que percorre a linha que a alimenta. Então:
Uf = U3 e If = I
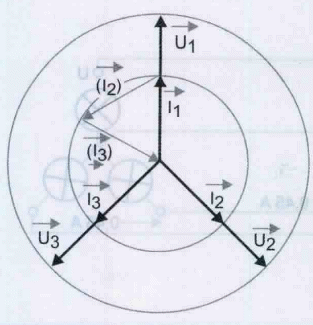
Se o sistema for equilibrado no neutro, não passa corrente porque tendo os receptores resistências, na representação vetorial, figura 10, as três estão em fase com as respectivas tensões e, somando-se os três vetores confirma-se que IN = 0. Para que o sistema seja equilibrado as correntes têm que ter o mesmo valor eficaz e igual desfasamento em relação às tensões respectivas, neste caso o neutro pode ser suprimido.
Se em lugar das resistências tivermos três bobinas iguais, então o desfasamento não seria nulo, como podemos verificar na figura 11, mas continuaremos a ter a corrente no neutro nula.
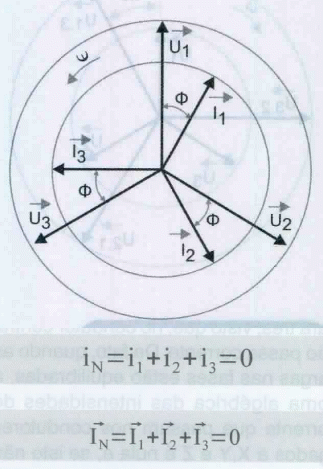
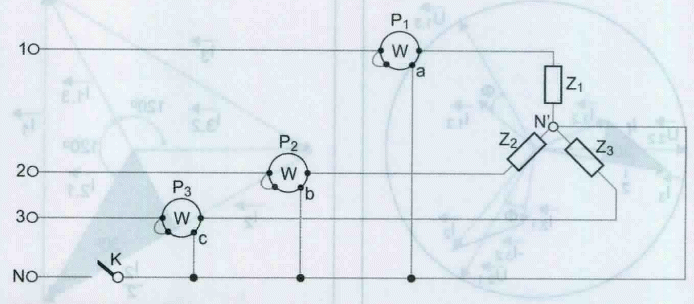
Se as três fases não são idênticas, as correntes nas três fases constituem um sistema trifásico desequilibrado, a sua soma não é nula, o condutor neutro é percorrido por uma corrente diferente de zero e não pode ser suprimido. Se suprimirmos o neutro as tensões nos terminais dos receptores deixam de constituir um sistema equilibrado, as fases são então submetidas a tensões superiores ou inferiores a US. Em um sistema desequilibrado, com os receptores ligados em estrela o neutro é indispensável, a intensidade de corrente no neutro pode ser determinada vetorialmente.
I1 = U1 / Z1
I2 = U2 / Z2
I3 = U3 / Z3
Na figura 12 está representado as correntes de um sistema desequilibrado e, como se pode verificar, as correntes desequilibradas originam um corrente do neutro não nula.
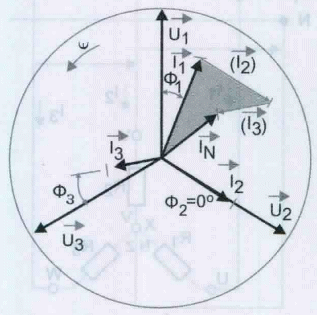
Num sistema desequilibrado, quando falta o neutro verifica-se as seguintes situações:
• A carga que tiver menor impedância será percorrida por maior corrente e terá uma tensão aplicada mais elevada, portanto maior Us:
• A carga que tiver maior impedância será percorrida por menor corrente e terá aplicada a menor das tensões, portanto menor Us;
• Podemos ter duas tensões maiores que Us ou, pelo contrário, uma tensão maior que Us e duas menores.
Conclui-se que o neutro é indispensável quando as cargas são desequilibradas, para evitar os desequilíbrios de tensões nas cargas e reduzir os desequilíbrios das correntes.
Ligação em triângulo
Na ligação em triângulo dos receptores, cada uma das três cargas é ligada entre duas fases diferentes, havendo sempre uma fase que é comum a duas cargas, conforme se pode verificar na figura 13.
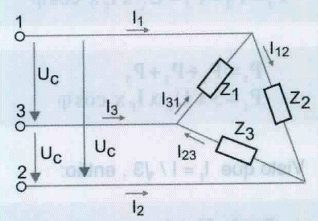
Deste modo cada carga fica submetida à tensão composta UC da rede, não existindo condutor de neutro nem tensão simples. Neste tipo de ligação podemos ter cargas equilibradas ou desequilibradas.
Na ligação em triângulo equilibrado cada carga fica submetida a tensões compostas iguais, tendo cada uma a mesma impedância (Z1 = Z2 = Z3) e o mesmo fator de potência (cos Φ1, = cos Φ2 = cos Φ3).
Na figura 14 está representado três cargas ligadas em triângulo equilibrado, as tensões U12, U23, U31, são as três tensões compostas iguais em valor eficaz, em representação vetorial, estas tensões estão desfasadas entre si 120°, visto que, constituem um sistema trifásico de tensões.
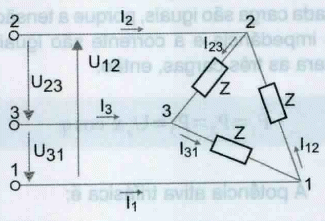
Conhecendo as tensões e as impedâncias, calculamos as correntes das cargas, I12, I23, I31 = UC, pela seguinte fórmula:
I12 = I23 = I31 = Uc / Z
Na figura 15 está representado a relação entre as correntes nos receptores e, aplicando-se a lei de Kirchoff temos:
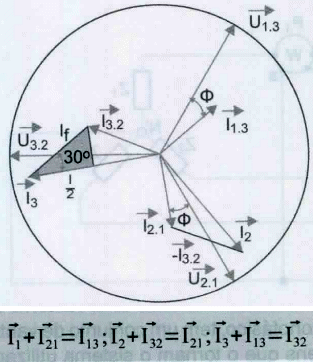
Efetuando a soma vetorial obtemos um triângulo de correntes que está representado na figura, na qual as correntes estão desfasadas entre si de 120° e 30° das correntes das fases. Ao analisar a figura 16 podemos tirar as seguintes equações, como a corrente I21 é a hipotenusa do triângulo retângulo e I2/2 é o cateto, temos:
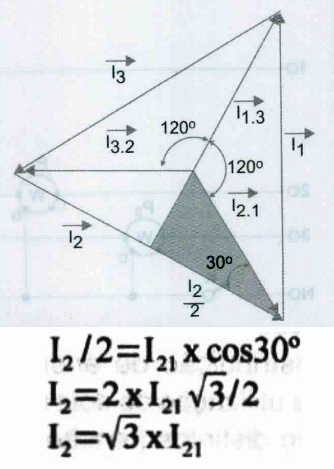
De um modo geral podemos designar I à corrente na linha de alimentação dos receptores, assim no caso de sistemas equilibrados será I = raiz(3)
Uma carga ligada em triângulo está desequilibrada quando as impedâncias (Z1, Z2, Z3) não são iguais e quando os fatores de potência das cargas são diferentes. Visto que as tensões compostas são iguais, impostas pela rede, então as correntes nas cargas diferem entre si, acontecendo o mesmo nas correntes das linhas, que são a soma vetorial das correntes das cargas.
As correntes nas cargas são obtidas pelas seguintes equações:
I12 = Uc / Z1
I23 = Uc / Z2
I31 = Uc / Z3
As correntes nas linhas são obtidas vetorialmente pelas seguintes equações:
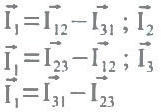
Podemos concluir que em triângulo desequilibrado não se verifica a relação entre correntes I = raiz(3) que só é válida para cargas equilibradas. As correntes nas linhas só podem ser obtidas vetorialmente. O sistema trifásico relativamente ao monofásico, tem um conjunto de vantagens que o tornam o sistema utilizado na produção, transporte e distribuição de energia elétrica.
• Na produção de energia, o alternador trifásico produz mais de 50% de energia do que um monofásico, pois aproveita melhor o seu circuito ferromagnético.
• No transporte de energia o sistema trifásico tem menos perdas e necessita de menos material acessório, sendo, portanto, mais rentável.
• Na distribuição de energia permite a utilização de dois níveis de tensão distintos (tensão simples e tensão composta), permite a utilização pelo consumidor do motor trifásico assíncrono, que é um motor barato, robusto.
Potências trifásicas
As potências ativa e reativa de uma carga, são sempre obtidas pelo produto entre a tensão (UZ) aplicada à carga, a corrente (lZ) que a percorre e o cos (1) ou sen Φ.
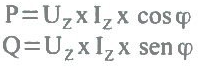
Visto que um sistema trifásico é constituído por três cargas, para obter as potências totais temos que somar as potências parciais respectivas, então:
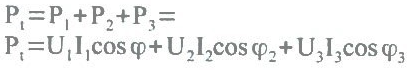
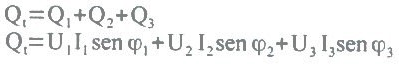
No caso das potências reativas, a soma é algébrica porque as bobinas têm potência reativa positiva e o capacitar tem potência reativa negativa. A potência aparente trifásica é dada por:
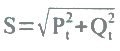
Se o sistema trifásico é em estrela e equilibrado, as potências ativas em cada carga são iguais, porque a tensão, a impedância e a corrente são iguais para as três cargas, então:
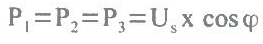
A potência ativa trifásica é:
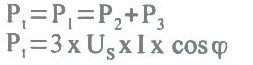
Visto que US = 43, então:
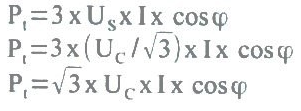
Em que 1 é a corrente da linha que é igual à corrente da fase na ligação em estrela.
De igual modo, a potência reativa é dada por:
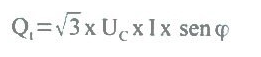
E a potência aparente é dada por:
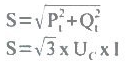
Se o sistema trifásico é em triângulo equilibrado, as equações das potências ativa, reativa e aparente são:
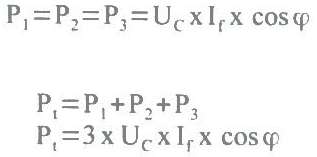
Visto que If = I/raiz(3), então:
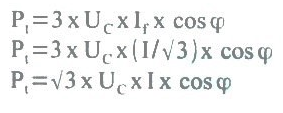
Em que I é a corrente da linha, que é diferente da corrente da fase na ligação em triângulo.
De igual modo, a potência reativa é dada por:
E a potência aparente é dada por:
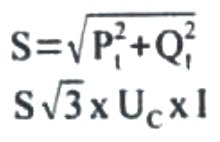
Medida de potências trifásicas
A obtenção das potências trifásicas em laboratório pode ser feita utilizando métodos diferentes, para os sistemas equilibrados e desequilibrados e ainda em função do número de wattímetros utilizados.
Método de um só wattímetro
Este método é utilizado apenas em circuitos trifásicos equilibrados, medindo-se a potência numa das cargas, multiplicando-se o resultado por três. Na figura 17 está representado a ligação do wattímetro, para medir a potência numa carga num sistema trifásico equilibrado em estrela.
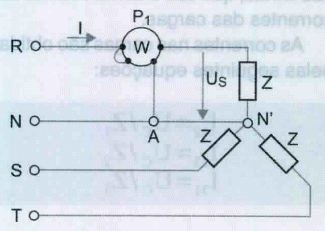
A equação da potência total é a seguinte:
Pt = 3 x P1
Método dos três wattímetros
Este método pode ser utilizado em sistemas equilibrados como em sistemas desequilibrados, utilizando três wattímetros.
Cada wattímetro mede a potência consumida por cada carga, sendo a potência total a soma das potências dos três wattímetros. Na figura 18 está representada a ligação dos três wattímetros.
A equação da potência total é a seguinte:
Pt = P1 + P2 + P3
Método do wattímetro trifásico
Este wattímetro permite medir diretamente a potência trifásica, em sistemas equilibrados ou desequilibrados, tendo no seu interior todo o equipamento necessário para medir a potência em cada carga, ou seja, é constituído pelo equipamento elétrico de três wattímetros monofásicos.
Método dos dois wattímetros
Este método também designado de método de Aron, utiliza dois wattímetros para medir a potência trifásica. Na figura 19 está representada a ligação dos wattímetros.
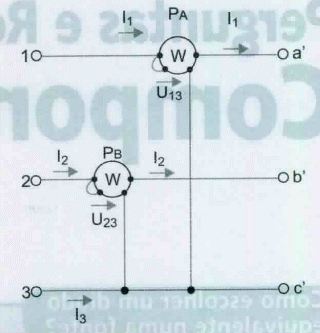
Os wattímetros medem as correntes de duas fases, através das suas bobinas amperimétricas, as bobinas voltimétricas são submetidas a tensões compostas diferentes, sendo uma das fases comum. A fase comum é aquela em que a corrente não percorre a bobina amperimétricas de nenhum wattímetro.
Este método é utilizado em sistemas equilibrados e desequilibrados, com as cargas em estrela ou em triângulo. Se a carga estiver ligada em estrela o condutor neutro deve estar desligado, porquê de outro modo escoar-se-ia alguma energia pelo neutro em caso de cargas desequilibradas, que não seria medida por nenhum wattímetro. Não podemos utilizar este método se o neutro dor indispensável na instalação.
Como pode ser utilizado em cargas equilibradas ou desequilibradas sem neutro, as leituras dos dois wattímetros podem ser iguais ou diferentes entre si, sendo assim três tipos de situações podem acontecer:
• Os ponteiros dos dois wattímetros desviam-se no sentido da escala (para a direita), neste caso a potência trifásica é obtida pela soma das duas leituras, ou seja:
Pt = PA + PB
• Os dois ponteiros deslocam-se para fora das escalas (para a esquerda), neste caso devemos inverter as ligações das bobinas amperimétricas para que os ponteiros se desloquem para dentro das escalas, de modo a podermos medir as potências.
A potência trifásica é dada pela equação anterior.
• Um dos ponteiros desloca-se para fora da escala, neste caso trocam--se as ligações da bobina amperimétricas respectiva, de modo a que o ponteiro se desloque para o interior da escala. A potência trifásica é dada por:
Pt = |PA – PB|
Não é importante qual dos wattímetros se desloca para fora da escala, porque a potência trifásica é sempre dada pela diferença entre a maior e a menor das potências, portanto positiva.
Compensação trifásica
A compensação do fator de potência em circuitos trifásicos é a de reduzir a potência reativa total da instalação, diminuindo o valor da corrente absorvida à rede.
A compensação trifásica é constituída por vários receptores trifásicos, consiste em ligar à rede três capacitores iguais, ligados em estrela ou em triângulo.
Geralmente é utilizada a ligação em triângulo dos capacitores, visto que, conduz a terem uma capacidade inferior à que seria necessário se eles fossem ligados em estrela. Os capacitores, em triângulo, ficam submetidos à tensão composta pelo que a sua tensão nominal é √3 vezes maior do que em estrela.