Na indústria, em equipamentos de precisão e em aplicações embarcadas encontramos uma infinidade de aplicações em que são usadas engrenagens cilíndricas de dentes retos. Se bem que exista uma boa quantidade de artigos que ensinem a calcular de forma simplificada essas engrenagens, as aplicações que envolvem precisão não aceitam as aproximações que são feitas em muitos casos. Neste artigo, abordamos de uma forma mais profunda o cálculo de engrenagens cilíndricas, de maneira muito mais apropriada às aplicações que envolvem precisão.
MEC292S
Na maioria das aplicações simples que envolvem o uso de engrenagens cilíndricas, o cálculo das engrenagens e da redução partem de aproximações que não correspondem à realidade. Conforme mostra a figura 1, parte-se do princípio de que a altura do dente pode ser desprezada, de modo que tenhamos apenas um diâmetro para cada engrenagem a ser considerado. Na prática, entretanto, as engrenagens possuem dentes com uma altura finita que deve ser considerada nos cálculos. Assim, o número de elementos que entra num cálculo de engrenagem é muito maior do que os poucos elementos que são utilizados em um cálculo simplificado.
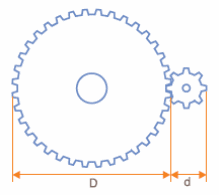
A ENGRENAGEM REAL
Na figura 2 temos a representação de uma engrenagem cilíndrica real. Os diversos elementos que devem ser considerados num cálculo são: N – número de dentes De – diâmetro externo m – módulo
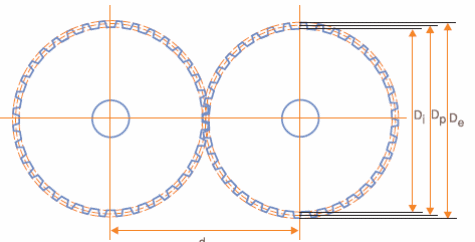
Dp – diâmetro primitivo
Di – diâmetro interno
h – altura do dente
ha – altura da cabeça
hb – altura do pé do dente
p – passo.
Assim, podemos definir “módulo de uma engrenagem” (m) como a relação entre o diâmetro primitivo (Dp) e o seu número de dentes (N):
m = Dp/N
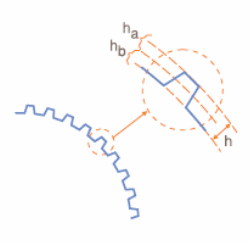
A partir do módulo podemos calcular as demais dimensões de uma engrenagem. O módulo também é muito importante na manufatura de uma engrenagem, pois é a partir dele que é determinada a ferramenta de fresagem a ser usada. Evidentemente, podemos fazer cálculos que envolvam as características de uma engrenagem partindo de outros dados. Observe que a altura total (h) do dente de uma engrenagem é dada pela soma da altura do dente (ha) mais a altura do pé do dente (b), observe a figura 3.
h = ha + hb
Outras fórmulas importantes que podem ser usadas no cálculo são:
De = Dp + 2m
De = m (N + 2)
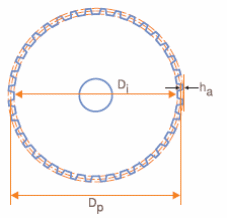
DIÂMETRO INTERNO
O diâmetro interno (Di) é calculado pela seguinte fórmula:
Di = Dp – 2hb
A figura 4 mostra como esse diâmetro é representando numa engrenagem.
CÁLCULO DO PASSO
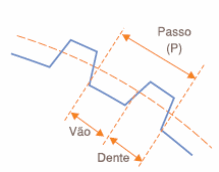
Conforme ilustra a figura 5, o passo é dado pelo arco de circunferência do diâmetro primitivo (Dp) que corresponde a um dente mais um vão da engrenagem. Podemos calcular esse arco, medido em radianos, a partir do diâmetro primitivo e o número de dentes usando a seguinte fórmula:
p = (Dp x π)/N
Em função do módulo (m), podemos também escrever:
p = m x π
DISTÂNCIA ENTRE EIXOS
As engrenagens são usadas em conjuntos como, por exemplo, em sistemas de redução e transmissão de movimento. No acoplamento de engrenagens, um dado importante é a distância entre eixos, pois ela determina exatamente o seu acoplamento, fixando o contato entre os dentes das engrenagens. Note que um contato imperfeito poderá causar esforços capazes de danificar uma engrenagem.
O cálculo da distância entre os eixos tem por referência o ponto de contato entre as engrenagens, veja a figura 6. A distância entre os centros (D) é dada pela soma da metade do diâmetro primitivo da primeira engrenagem com a metade do diâmetro primitivo da segunda engrenagem. Podemos escrever a seguinte fórmula para esse cálculo:
D = Dp1/2 + Dp2/2 ou D = (Dp1 +Dp2)/2
É importante observar que duas engrenagens acopladas têm sempre o mesmo módulo.
CONCLUSÃO
No cálculo de engrenagens que envolvam aplicações de precisão, as medidas que indicamos neste artigo devem ser consideradas. Observe que tudo é uma questão de geometria e que os cálculos envolvem fórmulas simples. No entanto, como em qualquer cálculo é preciso manter a coerência das unidades.



















