Nossos projetos para as Feiras de Ciências prosseguem cada vez com maior audácia. Os artigos de junho, julho e agosto foram um sucesso! Os alunos de 12 e 22 graus (e bom número de professores) manifestaram-se com suas sugestões e pedidos. E você, não vai participar?
Nota: Artigo publicado originalmente na revista Eletrônica Total 60 de 1993
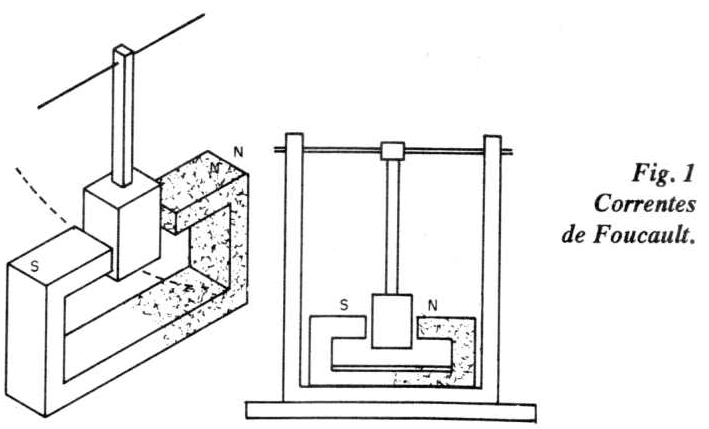
PROJETO 1: Correntes de Foucault
Material: - Ímã permanente em forma de U ou C, suporte e placa de alumínio (cobre, latão).
Observe a frenagem da placa de alumínio, quando posta oscilar entre os polos do ímã. Quando uma placa metálica oscila, cruzando o entreferro do ímã, ocorre uma variação de fluxo através da placa, determinada por uma variação de área. Essa variação de fluxo magnético induz uma f.e.m (força eletromotriz) na placa, que por sua vez, determina o aparecimento de uma corrente elétrica na massa de alumínio. Essa corrente induzida gera um novo campo magnético que se opõe ao campo magnético indutor (lei de Lenz).
Disso resulta a frenagem da placa. Esse efeito é usado para a frenagem do movimento de trens (sistema de freios eletromagnéticos). Essa corrente induzida na massa de metal é indesejável nos núcleos de transformadores. Para minimizar isso, o núcleo é construído com lâminas de ferrosilício isoladas entre si, para restringir o percurso dessas correntes.
Na figura 1 temos a ilustração dessa montagem.
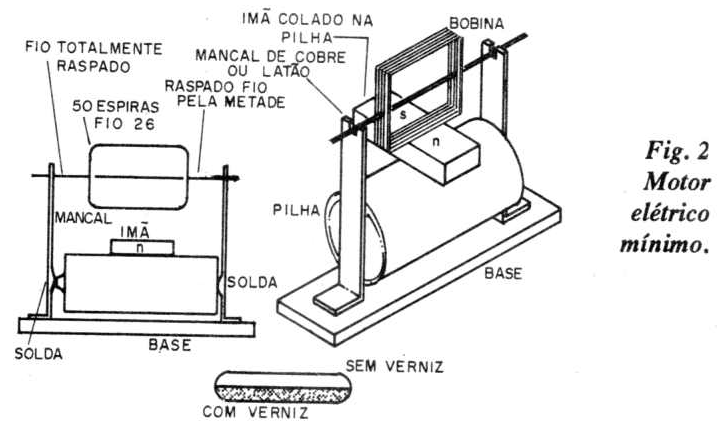
PROJETO 2: Motor Elétrico Mínimo
Material: pilha grande, fio de cobre esmaltado número 26 a 30 AWG, ímã permanente (em barra ou U), tiras com largura de 1,5 cm de cobre ou latão. Na figura 2 ilustramos a montagem.
Um dos terminais da bobina (50 espiras), que também serve de eixo, deve ter seu esmalte totalmente raspado. O outro terminal terá seu verniz raspado apenas "de um lado" do fio. A face raspada permitirá a passagem da corrente elétrica pela bobina, que então produzirá seu torque; o lado não raspado, isolado, interrompe a corrente na próxima meia volta.
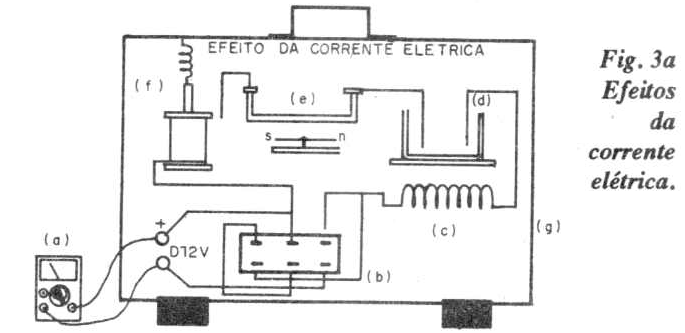
PROJETO 3: Efeitos da Corrente Elétrica
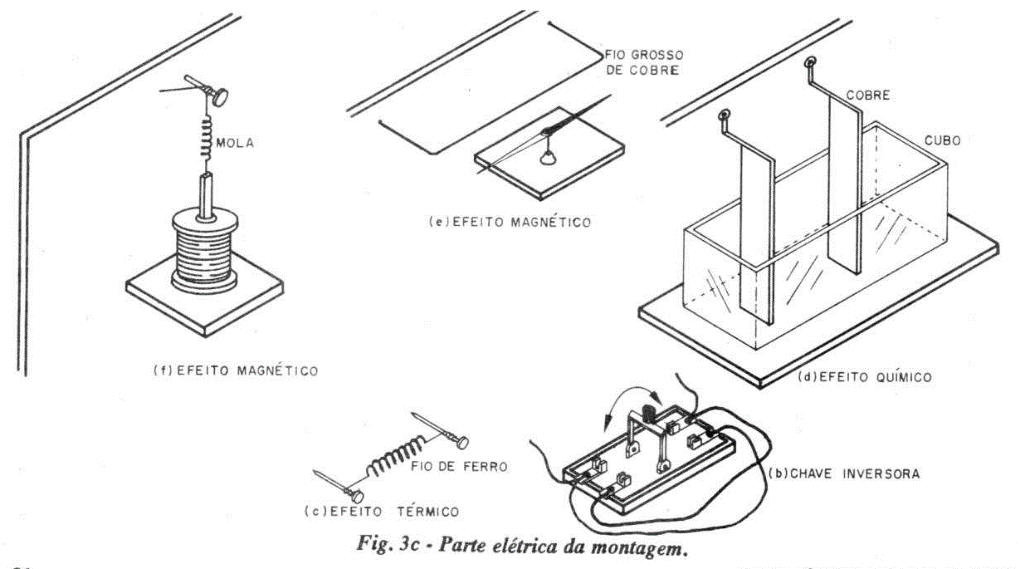
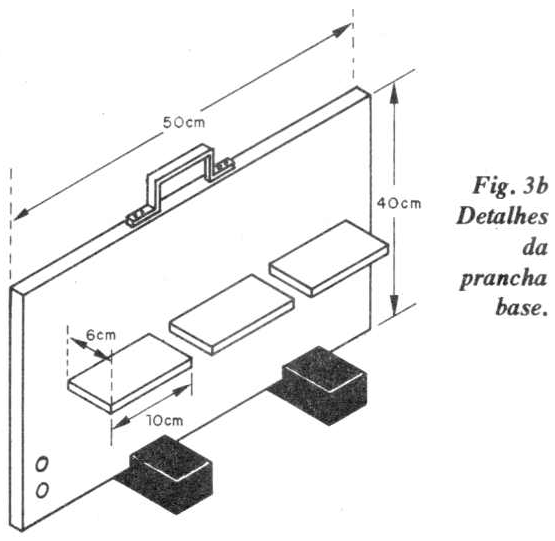
A prancha, com a montagem proposta na figura 3, permite colocar em destaque alguns efeitos da corrente elétrica.
Eis o material necessário:
(a) - fonte de tensão elétrica ajustável (0-12 Vc.c., 2A);
(b) - chave inversora 2x2, tipo faca;
(c) - fio de ferro, comprimento 90 mm, diâmetro 0,2 mm;
(d) - cuba de vidro de (5x5x10) cm, com duas placas de cobre imersas numa solução de sulfato de cobre (10%);
(e) - bússola ou agulha magnética montada sobre eixo vertical;
(f) - eletroímã (100 espiras de fio esmaltado 28 AWG sobre carretel de madeira - tipo costura) com núcleo solto e suspenso por uma mola;
(g) - tábua envernizada de (50x40x1) cm com pés e 3 placas de madeira de (6x10x1) cm;
(h) - fios de ligação (encapado e rígido, número 16 AWG), parafusos, etiquetas etc.
Ao aplicar-se tensão elétrica aos terminais (+) e (-), e com o fechamento da chave inversora para um dos lados, observa-se:
1 - O fio de ferro aquece-se ao rubro, mostrando o efeito térmico da corrente elétrica - o efeito luminoso associado é uma consequência do efeito térmico.
2 - Há um depósito de cobre metálico sobre a placa negativa, enquanto que na positiva tem-se uma parcial dissolução - é o efeito químico, visualizado pela eletrólise.
3 - A agulha magnética desvia-se de sua direção original (N-S), ficando quase perpendicular ao fio de cobre que está sobre ela - é o efeito magnético, invariavelmente associado a qualquer tipo de corrente elétrica.
4 - O núcleo de ferro (prego, parafuso) suspenso pela mola é atraí- do para o interior da bobina - novamente o efeito magnético.
Mediante a chave 2x2, inverte-se o sentido da corrente elétrica no circuito. Observe novamente os efeitos. Note as inversões em (d) e (e).
PROJETO 4: A Bailarina Equilibrista
Nesse projeto de Estática necessitaremos de uma rolha, uma vareta de madeira roliça (dessas usadas para churrasquinhos), uma esfera de aço (diâmetro 1 cm), um alfinete pequeno e uma figura de bailarina recortada em cartolina.
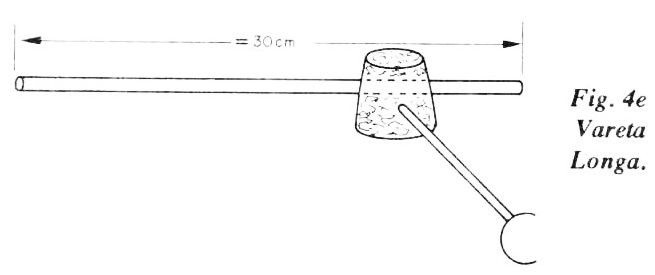
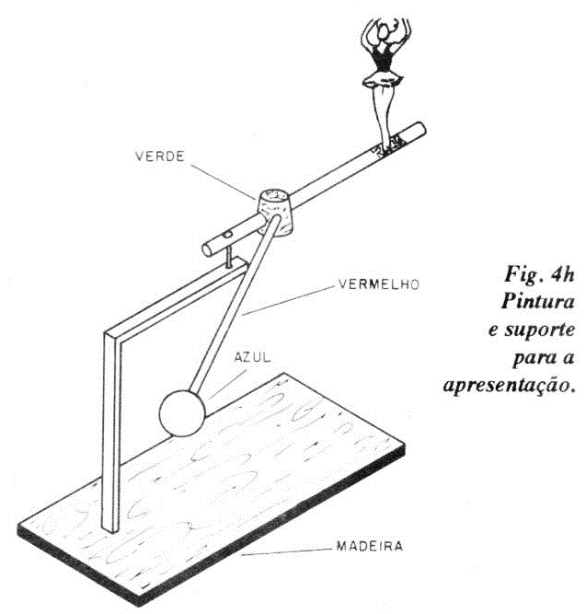
(a) - A figura 4.a. ilustra o aspecto final da montagem. Eis alguns detalhes:
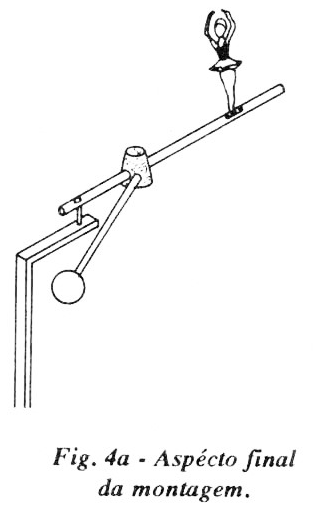
(b) - Com broca de diâmetro ligeiramente inferior ao diâmetro da vareta de madeira, fure de lado a lado a região mais estreita da rolha. Com a mesma broca, fure "diagonalmente a rolha até pouco mais de sua metade.
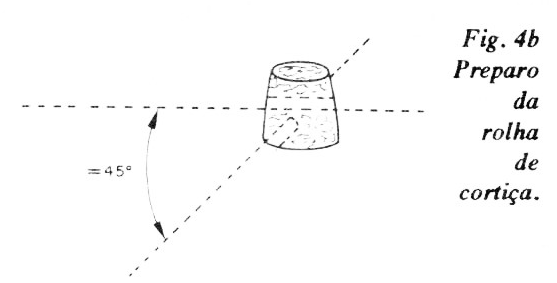
(c) - Corte 10 cm da vareta e espete no furo "diagonal" da rolha. Uma gotinha de "Super Bonder" resolve o problema de fixação.
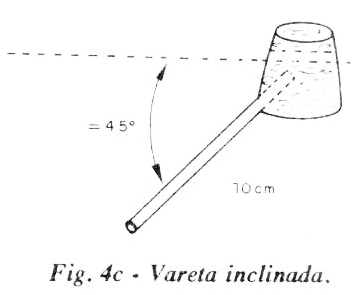
(d) - Ponha uma gota de "Super Bonder" na extremidade livre dessa varetinha e cole na esfera de aço. Segure firme até secar. Ponha uma ou duas gotinhas na junção vareta-esfera para garantir a fixação.
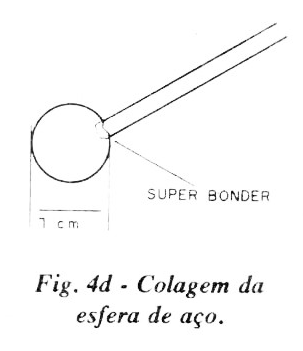
(e) - Passe o restante da vareta (cerca de 30 cm) através da rolha, no orifício já preparado. Não use cola, pois falta o ajuste final.
(f) - A 0,5 cm da extremidade da vareta (da esquerda, na figura), espete o alfinete até o fim. Quando a cabeça do alfinete encostar na vareta, ponha aí uma gota de "Super Bonder".
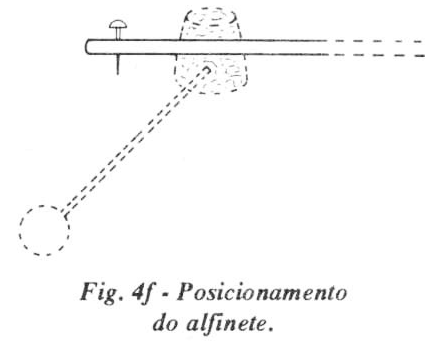
(g) - Recorte a figura da bailarina em cartolina colorida e fixe na outra extremidade da vareta.
(h) - Ajuste final. Apoie o alfinete na borda de uma régua ou quina de uma mesa e ajuste a distância da rolha ao alfinete até que, no equilíbrio, a vareta longa fique na horizontal. Obtida a posição final da rolha, fixe-a com uma gota de cola. Eis sua bailarina equilibrista em linda situação de equilíbrio estável. Difícil de acreditar, não?
PROJETO 5: "Marimba" de Vidro
A marimba proposta ("xilofone", para alguns), com lâminas de vidro, produz os sons de uma gama natural (dó, ré, mi, fá, sol, lá, si, do) na escala de Zarlino. É um projeto interessante, que lhe permitirá expor os sons da gama musical, suas frequências relativas, as lâminas vibrantes, as dependências entre as frequências e as dimensões das lâminas etc.
Uma lâmina metálica ou de vidro, que apresenta largura pequena em comparação com seu comprimento, fixada por uma das extremidades (ou apoiada por dois cordéis tensos na horizontal), vibra devido à sua elasticidade quando percutida com um martelinho de madeira (ou de borracha).
Se várias lâminas são do mesmo material (de vidro, por exemplo), de mesma espessura e de mesma largura, as alturas (frequências) dos sons que produzirão, quando percutidas, serão inversamente proporcionais à raiz quadrada de seus comprimentos.
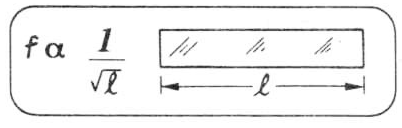
Desejando-se obter os sons da gama musical da escala natural, cujas frequências relacionam-se com a frequência fundamental mediante a série:
|
1 |
9/8 |
5/4 |
4/3 |
3/2 |
5/3 |
15/8 |
2 |
|
do |
ré |
mi |
fá |
sol |
lá |
si |
do |
os comprimentos das lâminas deverão estar como as raízes quadradas dos inversos dos números da série acima, ou seja:
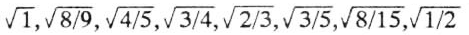
que valem, aproximadamente: 1 0,94 0,90 0,87 0,81 0,78 0,73 0,71
Desse modo, se a primeira lâmina de vidro da nossa marimba produz o dó fundamental com comprimento de 15 cm, as demais lâminas deverão ter:
14,10 cm; 13,50 cm; 13,05 cm; 12,15 cm; 11,70 cm; 10,95 cm; e 10,65 cm.
Após essa introdução teórica bem resumida, vejamos o material para a execução desse bonito trabalho escolar:
- 1 caixa de madeira (de 40x20x10) cm;
- 2 cutelos (prismas) de madeira de base 1 cm, comprimento 10 cm e altura 1 cm;
- 2 cordéis (cordonês) de 40 cm de comprimento;
- 8 lâminas de vidro plano comum, de 2 a 3 mm de espessura, 3 cm de largura e comprimentos de 15,00 cm; 14,10 cm; 13,50 cm; 13,05 cm; 12,15 cm; 11,70 cm; 10,95 cm e 10,65 cm;
- 1 martelinho com ponta de borracha;
- 4 pequenos pitões.
Um bom vidraceiro, com seu "diamante", poderá lhe fornecer tais lâminas com boa precisão nos comprimentos. Se você lhe contar que é para um trabalho científico, com certeza ele caprichará mais ainda, polindo as laterais das lâminas, ajustando as medidas feitas com um paquímetro e eliminando as arestas "vivas". Cuidado com tais arestas "vivas" de vidro, pois podem produzir cortes profundos na pele.
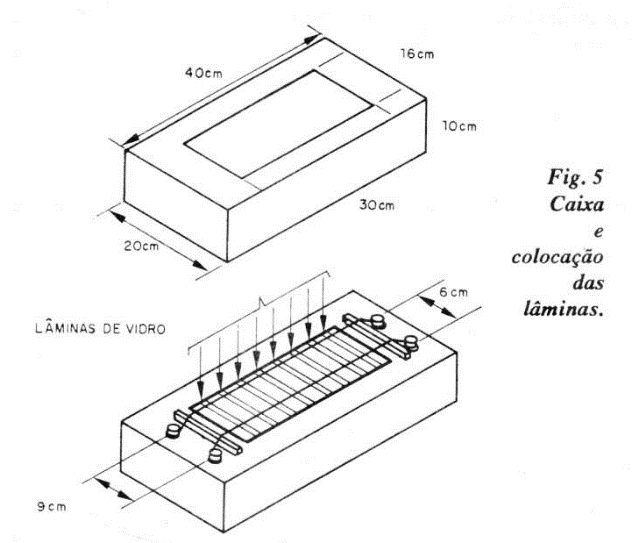
Na figura 5 temos o aspecto final da montagem.
Os dois prismas de madeira que elevam os cordéis, esticando-os, são fixados (colados) no tampo da caixa a 35 cm um do outro. Os dois cordéis são amarrados e esticados entre os pitões enroscados na madeira da caixa. Os pitões do lado da lâmina maior distam 9 cm um do outro e, os do outro lado, 6 cm. Disponha as lâminas sobre os cordéis, a 1 cm uma da outra.
Obtidas as disposições corretas das lâminas sobre os cordéis, use "Super Bonder" para fixar as lâminas nos cordéis. Agora é só preparar seu "box" com os cartazes devidos e executar bonitas melodias com seu científico instrumento musical.
PROJETO 6: Figuras de Lissajous, em 3 Dimensões
As figuras de Lissajous são resultantes de superposições de dois movimentos harmônicos que se desenvolvem em direções perpendiculares.
Você pode obter tais figuras projetadas em uma tela, por efeito da persistência retiniana, de vários modos, tais como:
(a) - Colar dois pequenos espelhos planos em uma das extremidades livres de dois diapasões que vibram em planos perpendiculares e incidir um estreito pincel de luz (de preferência, de laser) que, refletindo-se em ambos os espelhos, incida na tela. Esse pincel de luz "pinta" na tela a figura de Lissajous.
(b) - Colar dois pequenos espelhos planos nos centros de dois cones de alto-falantes, dispostos em planos perpendiculares, e incidir um feixe de luz laser que, refletindo-se em ambos os espelhos, atinge a tela. Essa técnica é mais aprimorada que a anterior, pois esses alto-falantes poderão ser excitados por pequenos amplificadores de áudio (5 a 10 W), cada um deles, por sua vez, excitados por geradores de audiofrequência independentes. Os devidos ajustes das frequências componentes, assim como suas amplitudes, permitem visualizar na tela (duas dimensões) toda a gama de figuras de Lissajous.
Nosso projeto permite a visualização de tais figuras em três dimensões. É um trabalho audacioso para alunos do segundo grau, que, porém, deve ser tentado. Vencer desafios é a meta do ser humano culto e integrado na educação. Em tempo, sempre é bom alertar que ninguém "tem educação", pois educação é um processo, não um fim.
Vejamos a ideia básica do projeto. Você deve ver tais figuras de Lissajous, logo luz deve partir de algum lugar e incidir em seu globo ocular - necessitaremos de uma fonte de luz. Essa pode ser um projeto de "slides", um projetor de "loops", ou qualquer outra fonte colimada (dotada de lentes que permitam o ajuste da focalização).
Essa luz não poderá vir diretamente da fonte para seus olhos; ela deverá ser refletida (ou melhor, difundida) por "alguém" (superfície difusora) e a seguir dirigida para os olhos de vários observadores (e não só os seus!). Além disso, essa difusão de luz, para vários observadores, deverá produzir, por persistência retiniana, a figura de Lissajous em 3 dimensões - logo, já deve ser a resultante de movimentos harmônicos perpendiculares entre si.
Eis como pode-se obter tudo isso:
1) Um pequeno motor elétrico, cuja rotação possa ser controlada eletronicamente, leva em seu eixo um disco de madeira (pintado com tinta preta opaca) de 10 a 12 cm de diâmetro. Próximo à periferia desse disco, prende-se, perpendicularmente ao seu plano, uma haste cilíndrica de madeira, de diâmetro 0,6 a 0,8 cm e comprimento 10 e 12 cm, pintada com tinta branca (tinta látex, branco neve). Um lápis de cor, branco, pode ser usado sem problemas.
A figura 6.a. ilustra essa parte da montagem.
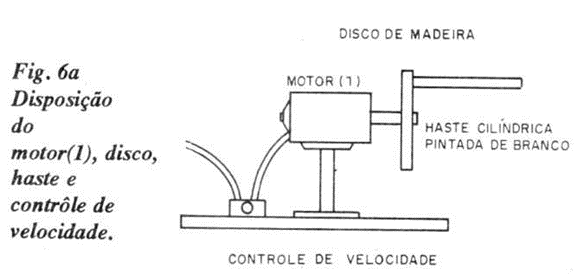
Ligando-se o motor elétrico, a haste branca põe-se a girar, descrevendo uma superfície cilíndrica, em relação ao eixo de rotação.
Se o período de rotação do eixo do motor for menor que 1/10 de segundo, não veremos a haste deslocando-se de uma posição para a outra e sim um "tubinho branco", devido à persistência retiniana.
Olhando-se tal "tubo", de lado, tal como se observa na figura 6.a., veremos apenas uma "faixa branca". Essa faixa branca nada mais é que a projeção do movimento da haste num plano vertical (plano zOy), que é um movimento harmônico simples (MHS) de frequência f (igual à do rotor do motor) e amplitude r (distância do centro do disco à haste). A figura 6.b. mostra o movimento da haste no plano zOy.
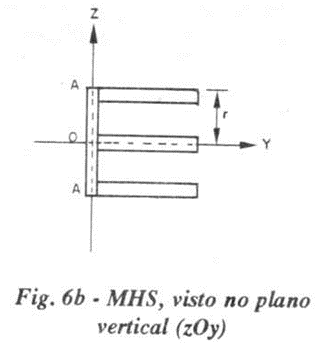
Visto desse plano, o movimento de um ponto de haste, no eixo de referência z, é dado pela equação:
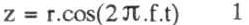
onde r é a amplitude do movimento, f sua frequência, z a elongação do ponto da haste, medida a partir do eixo de rotação, e t é o tempo. Assumimos a fase inicial nula, ou seja, a haste encontra-se na posição extrema A (+r) no instante ao qual se associa t=0.
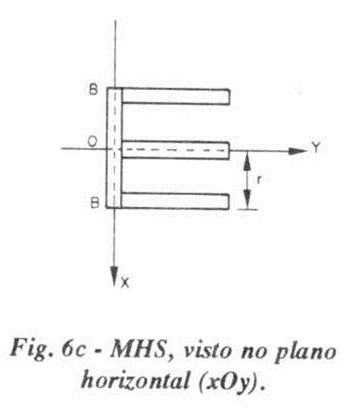
Se olharmos o movimento da haste por cima, ou seja, visto no plano xoy, também teremos um MHS de amplitude r, frequência f e defasado do movimento vertical (de equação 1) de π/2 radianos. Você deslocou seus olhos do plano vertical para o plano horizontal - deslocou-se de π/2 radianos. Matematicamente, no instante inicial já adotado o ponto da haste encontra-se em 0 e não em B. A figura 6.c. ilustra tal situação. A figura 6.d. mostra, em perspectiva, tais movimentos harmônicos simples.
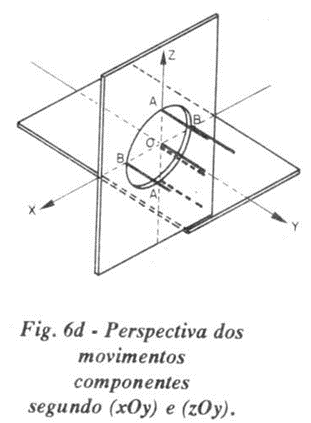
Esse movimento, visto no plano horizontal, tem equação:
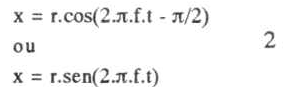
Superpondo-se esses dois movimentos harmônicos simples, de direções perpendiculares, mesma amplitude, mesma frequência e defasados de π/2 radianos, tem-se como resultado um movimento circular e uniforme de raio r e frequência f, que é o movimento de qualquer ponto da hás-te branca, no espaço. A haste toda descreverá, portanto, a superfície cilíndrica vista por persistência retiniana.
As equações 1 e 2 são as equações paramétricas desse MCU.
A trajetória resultante, de cada ponto da haste branca, tem equação obtida a partir de 1 e 2, com a eliminação do parâmetro t.

somando-se membro a membro:
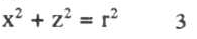
A 3 é a equação da circunferência de raio r e centro na origem do sistema de coordenadas (0).
Observe, portanto, que o simples movimento da haste ao redor do centro do disco já é a composição de dois movimentos harmônicos simples perpendiculares entre si, dando como visual, em alta rotação, o cilindro branco.
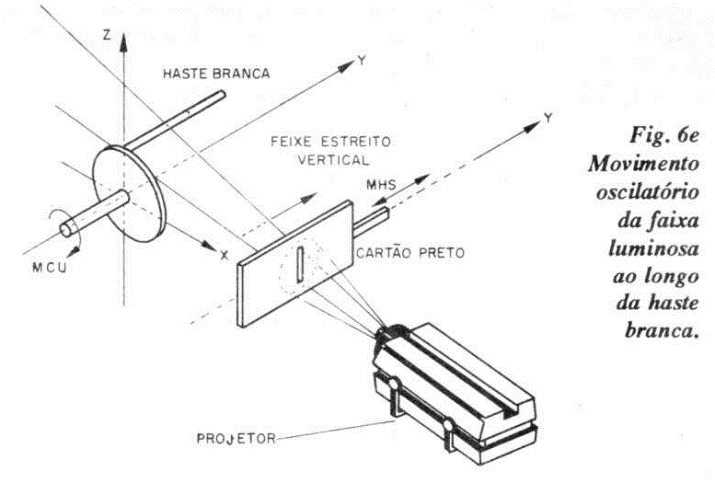
A seguir, vamos introduzir o terceiro movimento harmônico simples no sistema. Esse terceiro movimento harmônico será o de uma estreita faixa luminosa vertical, percorrendo a extensão da haste branca horizontalmente. A figura 6.e. ilustra a inclusão desse movimento no sistema.
Essa faixa luminosa vertical, em movimento harmônico horizontal, é obtida a partir de um cartão preto que contém uma fresta de 2 mm de largura por 5 cm de comprimento e que oscila na frente do feixe de luz proveniente do projetor.
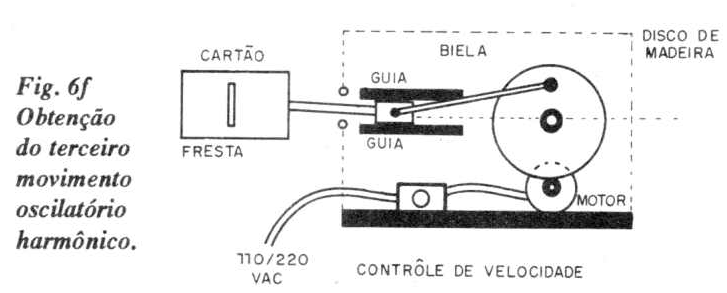
Esse movimento oscilatório do cartão pode ser conseguido de vários modos. Um deles, ilustrado na figura 6.f., consiste em converter o movimento circular de um disco (cuja periferia encosta no eixo de um motor elétrico) em um movimento harmônico através da técnica manivela-biela.
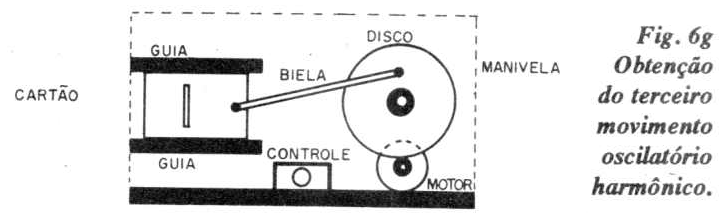
Outra solução é colocar guias para o movimento do cartão e ligar a biela diretamente no disco ao cartão, como ilustrado na figura 6.g. Optamos pela primeira solução por já encontrar-se pronta na fase de desenvolvimento desse projeto.
A rotação desse motor (cujo eixo revestido de borracha toca a periferia do disco) também é controlada eletronicamente (ver comentários adiante). Com essa montagem, a luz que passa pela fresta do cartão percorrerá a haste branca, ao longo de sua extensão (eixo y), com equação:
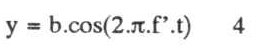
onde b é amplitude do movimento (cerca de metade do comprimento da haste; esse ajuste faz-se através das posições relativas entre fresta, haste e projetor) e f' é a frequência do movimento do cartão (ajustável no motor 2).
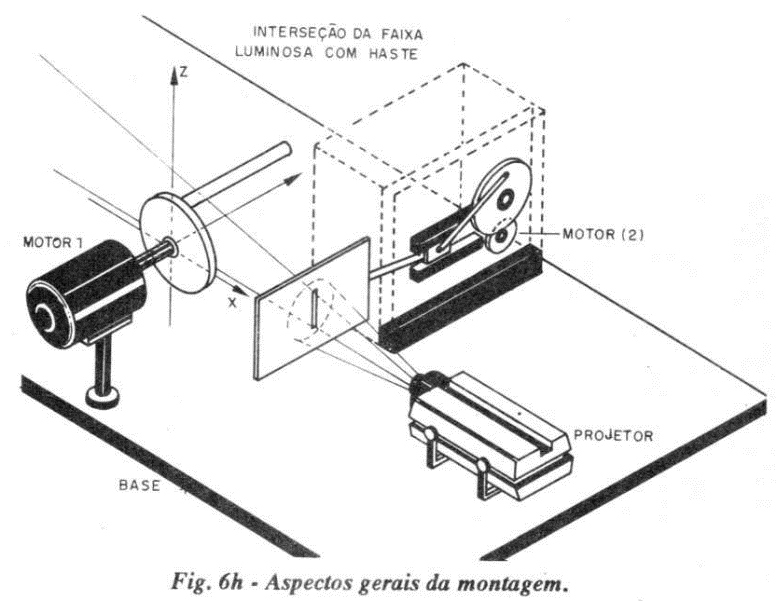
A figura 6.h. dá um visual geral da montagem.
Com a haste branca em repouso (motor 1 desligado) e com o cartão em movimento (motor 2 ligado), a faixa luminosa vertical percorrerá toda a extensão da haste branca num movimento de vai e vem (é o movimento dado pela equação 4); com o motor 1 ligado, observar-se-á a superposição dos 3 movimentos, de equações 1, 2 e 4, simultaneamente, pela luz difundida pela haste branca. Em ambiente escurecido o visual é surpreendente. A figura 6.i. exibe 2 desses visuais.
As equações:

são as equações paramétricas da figura de Lissajous em 3 dimensões. Essa figura estará contida na superfície do cilindro com base de raio r e altura 2b, como se ilustra na figura 6.i. Comentários: Alguns detalhes construtivos são postos, a seguir, no intuito de orientá-lo. Modificações técnicas são sempre possíveis, dependentes sempre dos recursos à disposição. Não se acanhe em pedir ajuda ao professor, aos familiares, ao marceneiro da rua, ao torneiro conhecido. Basta que você e seus colegas participantes do projeto conversem seriamente com tais pessoas, destacando o projeto científico.
Motores elétricos universais (dotados de escovas) para 110 V são os mais indicados para o projeto (tipo motor de máquina de costura, furadeiras elétricas manuais, peque-nos agitadores elétricos de cozinha etc), por admitirem ajuste eletrônico de velocidade. O circuito eletrônico mais simples para tais controles é o ilustrado na figura 6.j. Dois dimmers de luz, comerciais, resolvem os controles dos dois motores do projeto. Para a montagem do controle de velocidade (ou de potência) cujo esquema apresentamos, o material é o seguinte:
- 1 triac TIC-226D
- 1 diac comum
- 1 potenciômetro linear de 220 kΩ
- 1 resistor 3,3 kΩ x 1 W
- 1 capacitor de poliéster de 50 nF a 100 nF x 400 V
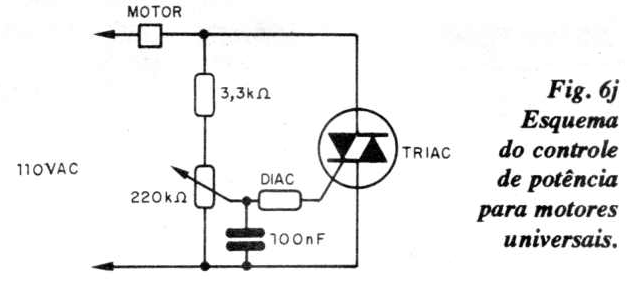
Esse controle, dado a sua simplicidade e número de componentes, pode ser montado numa pequena ponte de terminais ou, para montadores mais experientes, em uma placa de circuito impresso. O movimento do cartão com fresta vertical não precisa ser exageradamente rápido, daí a redução proposta, pela técnica de encostar o eixo do motor 2 na periferia do disco de madeira. Um tubinho de borracha ou plástico encaixado justo nesse eixo garante o atrito necessário ao não escorregamento.
Esse disco de madeira pode ter diâmetro em torno dos 12 cm; desse modo o pino da biela poderá ser ajustado para vários braços de manivela (modificação do raio) e, com isso, ajustar a amplitude do movimento. Desejamos total sucesso nesse empreendimento científico. Ele é recomendado para Feiras, Exposições e estudos em vários níveis de profundidade. O autor desenvolveu esse projeto em fins de junho de 1993 no. Laboratório de Demonstrações do Instituto de Física da Universidade de São Paulo, setor esse sob responsabilidade do Prof. Dr. Ernst W. Hamburguer. Colaboraram na elaboração do instrumental os técnicos Cidemar Divanir Forcemo e Wilson Luis da Silva.
Em tempo, tal projeto (e mais de 100 outros de igual importância ao desenvolvimento da Física Clássica) encontra-se à disposição de alunos e interessados, nesse Laboratório, de segunda a sexta, das 8 às 21 hs (IFUSP, ED.PRINCIPAL, ALA CENTRAL, LAB. DE DEMONSTRAÇÕES).