Com a disponibilidade de capacitores com capacitâncias muito grandes, os supercapacitores, é de grande importância para o praticante da eletrônica saber realizar cálculos com estes componentes. Neste artigo, abordamos alguns cálculos importantes com estes componentes.
Lembramos que estes cálculos têm seus fundamentos dados no nosso livro Aprenda Eletrônica – Curso Básico e em diversos artigos de nossa seção de Matemática Para Eletrônica. O leitor também pode encontrar toda essa teoria nos livros de física do ensino médio.
Importância
Nas aplicações atuais, os supercapacitores são usados basicamente como fontes de energia. Com capacitâncias da ordem de muitos Farads eles podem ser usados como fontes de energia em diversas aplicações.
No entanto, os supercapacitores de que dispomos hoje são dispositivos de baixa tensão, da ordem de poucos volts, o que leva à necessidade de fazermos sua associação no momento de uso. Da mesma forma, na carga desses componentes, essa limitação exige cuidados especiais.
Assim, o leitor que pretende utilizar supercapacitores associados como fontes de energia deve estar preparado para saber como eles se comportam num circuito, principalmente se tiverem valores diferentes.
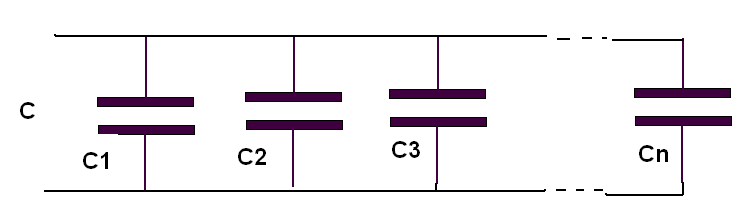
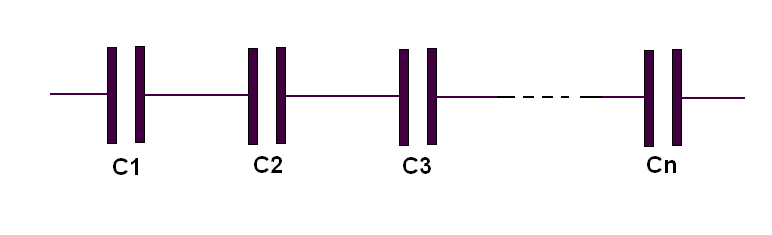
Assim, damos a seguir um exemplo de cálculo com supercapacitores, lembrando que na associação em paralelo, suas capacitâncias se somam, e na associação em série a capacitância equivalente é dada pela fórmula na figura 1:
Um cálculo prático:
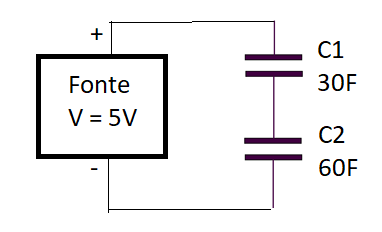
Vamos imaginar que o leitor consiga dois supercapacitores, sendo um de 30F e outro de 60F, ambos com tensão de 3,3 V, desejando usá-los num projeto em que eles alimentarão um circuito eletrônico.

Ocorre que pretendo carregá-los em série em uma fonte de 5V, pois certamente não poderei ligar capa um diretamente na fonte, pois os 5V são mais do que a tensão nominal que eles suportam. Temos então o seguinte circuito para a carga:

Veja que na prática não se recomenda a ligação direta da fonte nos capacitores descarregados, pois a corrente inicial representa um curto que pode danificar a fonte. Deve haver um circuito próprio que limite a corrente inicial a um valor seguro.
Uma vez carregados, vamos ligar os capacitores em paralelo, esperando que a tensão obtida se aproxime de 2,5 V (metade dos 5 V que esperamos ser a tensão da carga de cada um. Será que é isso que ocorre?
Começamos então por calcular a resistência equivalente que obtemos quando ligamos os dois capacitores em série, no processo de carga:
1/C = 1/30 + 1/60
Ou:
C = (C1 x C2) / (C1 + C2)
Fórmula simplificada quando temos dois capacitores. Obtemos:
C = (30 x 60)/(30 + 60)
C =1800/90
C = 20F
Voltando ao circuito de carga vemos então que a carga armazenada em cada capacitor será:
Q = C x V
Q = carga em Coulombs
C = Capacitância equivalente
V = tensão no circuito
Q = 20 x 5 = 100 Coulombs
Veja que uma propriedade importante da associação em série dos capacitores é que, independentemente dos valores dos capacitores associados, todos se carregam com a mesma carga.
É importante observar que as tensões também serão diferentes, o que no caso de capacitores de valores diferentes deve ser considerado, pois pode passar dos 2,7 V. Com o valor da carga o projetista pode calcular a tensão com que cada um se carregou.
No entanto, se os ligarmos em paralelo agora, as cargas vão se distribuir e uma determinada tensão aparecerá na associação em paralelo. Como calcular o valor?
A) Temos a carga em cada capacitor: 100 Coulombs
B) Temos a capacitância equivalente em paralelo (30F + 60F) = 90 F
A tensão será então:
V = Q/C
V = tensão
Q = carga
C = capacitância
V = 100/90
V = 1,11 V
Bem diferente do que se esperava. Por quê?
Fica claro nestes cálculos que os valores diferentes dos capacitores fizeram com que a distribuição da carga e da tensão não ocorresse por igual.
Assim, quando trabalhamos com supercapacitores ou mesmo eletrolíticos e eles devam ser associados, devemos estar atentos para essa distribuição desigual de cargas e tensões que ocorre com componentes de valores diferentes.
Uma pequena diferença de valor não afeta muito os resultados, mas uma diferença maior como a que ocorreu no exemplo dado levou a uma tensão muito menor do que a esperada no banco de dois capacitores.
Os mesmos cuidados devem ser tomados nos cálculos quando trabalhamos com bancos de muitos capacitores.
E, para os leitores que estão se preparando para um vestibular, um concurso em que se exija conhecimentos sobre capacitores no nível indicado, esta é uma questão que pode ser incluída.
Sugestões:
a) Faça os mesmos cálculos para dois supercapacitores de mesmo valor.
b) Haveria o perigo de um ou mais supercapacitores se queimar na carga pela tensão maior do que 2,7 V que apareceria entre suas armaduras? Calcule
c) Proponha para seus alunos cálculos envolvendo mais de dois supercapacitores.