No Monte um Computador Analógico (ART3212) ensinamos como montar um computador com potenciômetros e alguns componentes adicionais, cujo potencial de cálculo surpreendeu a muitos de nossos leitores. Nós mesmos temos o protótipo ainda montado o qual montamos num vídeo ((veja no final do artigo o link). Demos exemplos de diversos cálculos e até fizemos um curso que mostrava como usar este computador (Computação Analógica – Lição 1 – Os Computadores Analógicos (CUR6001) ). No artigo anterior fomos um pouco além mostrando alguns cálculos avançados que podem ser feitos com o computador analógico. Neste artigo continuamos como mais alguns cálculos interessantes que, certamente, muitos dos nossos leitores não poderiam imaginar que poderiam ser feitos com ele.
Sugerimos que os leitores vejam os artigos indicados na introdução e também Cálculos avançados com um computador analógico - 1 (DID021) para saber um pouco mais sobre o nosso computador analógico.
Calculando altura e distância
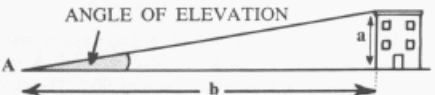
Problema: Sabe-se que um edifício está a 300 metros de distância. De um ponto ao nível da parte inferior do edifício, o ângulo de elevação do topo do edifício é 11° (Fig. 1). Qual a altura do prédio?

Defina 900 pés (a distância para o edifício) na escala M do potenciômetro X. Defina a escala N do potenciômetro Y em 11°. Achar a resposta da maneira usual na escala O do potenciômetro Z. O prédio tem aproximadamente 175 pés.
Por que isso funciona?
As escalas M, N e O são baseadas na relação:
tan A = a/b
Na Fig.1 um triângulo é mostrado em que a é a altura de um objeto distante no nível do solo, b é a distância ao objeto, e A é o ângulo de elevação do topo do objeto distante. A fórmula acima então se aplica. Pode ser reescrito na forma:
a = b tan A
ou Altura do Objeto = Distância ao Objeto X tan A
Observe que esta é da forma básica X Y = Z, em em que X é a distância até o objeto, Y é tan A (a tangente do ângulo de elevação ao topo do objeto) e Z é a altura do objeto.
Uma distância máxima de 5.000 pés foi selecionada para a escala M, que foi então marcada linearmente a partir de 0 a 5.000. Um ângulo máximo de 15 ° foi selecionado para a escala N.
As tangentes dos ângulos de 0 a 15° foram então marcados. Essas seleções foram feitas para conveniência. Outras distâncias e ângulos podem ter foi selecionado. Mas uma vez que estes foram escolhidos, os valores na escala O no potenciômetro Z foram determinados. Um cálculo mostrou que uma distância de 5.000 pés e um ângulo de 15° correspondia a uma altura de 1.340 pés. Esta distância foi, portanto, definida no ponto máximo da escala O no potenciômetro Z. Esta escala foi então subdividida em divisões iguais (linearmente).
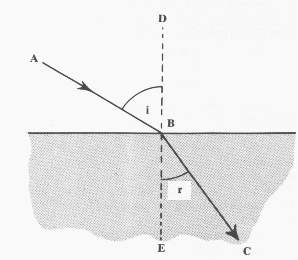
A Fig. 2 mostra um raio de luz se movendo na direção AB. Ela atinge uma superfície transparente, como vidro ou água (indicada pela área mais escura na Fig. 2). O raio dobra e assume uma nova direção (B C) dentro do novo material.
A quantidade exata de dobra é importante na concepção de instrumentos ópticos. Ao fazer cálculos, engenheiros fazem uso da Lei de Snell, que afirma:
sin i / sin r = n
Nesta fórmula, i representa o ângulo de incidência quando o raio de luz atinge um material transparente a partir do ar, (Fig. 2), r representa o ângulo de refração e n representa o índice de refração, um número que é diferente para os diversos materiais. Alguns típicos valores do índice de refração são indicados em
Tabela I.
ÍNDICE DE REFRAÇÃO
Vácuo 1,00
Air 1,0003
Água 1,33
Éter 1,35
Álcool (etil) 1,36
Álcool (eemil) 1,4
Peróxido de hidrogênio 1,41
Azeite de oliva 1,48
Vidro (corvo n) 1,51
Sal-gema 1,54
Quartzo 1.54
Terebintina 1,57
Vidro (pederneira densa) 1,71
Diamond 2.47
Há um fato interessante sobre esta fórmula que afetou o design das escalas em seu computador. Valores do índice de refração normalmente começam em 1 e vão até cerca de 2,5. A região de números de 0 a 1 foi, portanto, eliminada de seu computador. A escala P é baseada no seguinte modificação da Lei de Snell:
1/n x sin i = sin r
Isso agora se assemelha à forma X Y = Z, desde que 1/n seja marcado na escala para o potenciômetro X e o senos de ângulos marcados nas escalas para dos potenciômetros Y e Z. Observe a maneira como os números para o índice de refração aparecem na escala P.
No zero do ponteiro, observe o símbolo ∞, representando o infinito. Os números diminuem muito rapidamente à medida que você dá a volta na escala para a direita e finalmente termina no 1.
Na prática, números superiores a 2,5 não são necessários porque a maioria das substâncias tem índices de refração entre 1,3 a 2,5. No entanto, números foram incluídos porque podem ser interessante para ver o que aconteceria se outros índices de refração ocorrerem.
Uma maneira que os cientistas usam para identificar um material é medindo o índice de refração e comparando-o com os valores registrados em tabelas semelhantes à Tabela I.
Observe que o índice de refração do ar é muito perto de um vácuo. É suficientemente preciso para a maioria dos propósitos, supor que um raio de luz vindo do ar como se viessem do vácuo, e assim podemos usar 1,00 em nossos cálculos.
Problema: um raio de luz entra na água (do ar) em um ângulo de incidência de 62°. Qual é a sua nova direção na água?
Defina o índice de refração da água (1,33) na escala P do potenciômetro X.
Defina o ângulo de incidência (6 2°) na escala Q do potenciômetro Y. Encontre a resposta (ângulo de refração) na escala R do pote Z da maneira usual. O.
A resposta é cerca de 42°.
Em termos gerais, o índice de refração aparece na escala P do potenciômetro X. O ângulo de incidência aparece na escala Q do potenciômetro Y. O ângulo de refração aparece na escala R do potenciômetro Z.
Fórmulas trigonométricas
As seguintes funções trigonométricas contêm três variáveis da forma em que uma quantidade se multiplica por um segundo número é depois a um terceiro, podendo, portanto, ser resolvido com o seu computador.
Para fazer escalas adequadas, será necessário marcar comprimentos em proporção as funções trigonométricas obtidas numa tabela e depois reduzi-las para se ajustar à sua escala.
Aqui estão duas relações trigonométricas que pode ser colocado no seu computador.
tan a = sin a / cos a
sin 2a = 2 sin a cos a
Perímetro de um polígono regular
Algumas funções matemáticas envolvem combinações de três variáveis de maneiras complexas. Considere a seguir:
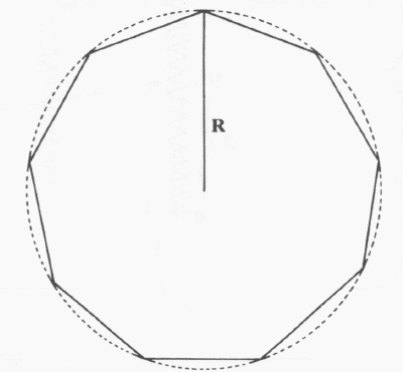
A Fig. 3 mostra um polígono regular, que tem todos lados e ângulos iguais. O perímetro (P) de tal polígono regular é dado pela fórmula:
P = 2nR sin (π / n)
R é o raio do círculo circunscrito (a distância do centro a um canto), e n é o número de lados.
Observe que existem três variáveis (P, n e R) e que eles estão todos conectados por multiplicação ou divisão de alguma maneira. Recombine as variáveis como segue:
P = 2 R [n sin(π / n) ]
Agora é temos algo semelhante à forma geral Z = CXY que pode ser colocado nas escalas de seu computador. Contudo, será necessário remarcar uma das escalas (X ou Y) em proporção a (n s> n ~) – Calcular (n sin —n) para uma série de valores de n, até cerca de 15. Em seguida, remarque as escalas.
Área de um polígono regular
A = (1/2)R2 x [n sin(2π/n)]
Veja a Fig. 3 e o problema anterior.
Decaimento radioativo
Substâncias radioativas "decaem" ou se transformam em outros materiais a uma taxa fixa. Uma porcentagem fixa permanece no final de um determinado período. Por exemplo, suponha que 10% de uma determinada substância se decompõe após um dia.
Diz-se que a constante de decaimento é 0,10 (por dia).
Comece com 1 libra de material. No final de um dia, a quantidade restante seria de 0,9 libras. No fim do segundo dia, o valor restante seria 0,9 X 0,9 ou 0,81. No final do terceiro dia, a quantia seria ser 0,9 X 0,9 X -9 ou 0,73. A fórmula em geral será:
A = (1 - d)t‘
A representa a quantidade restante após uma série de períodos de tempo (t), assumindo que o montante original é 1 e d representam a constante de decaimento radioativo.
Isso se assemelha muito à fórmula de juros compostos, A = (1 + i) n, exceto que diminuição que ocorre em vez do crescimento.
A função de decaimento radioativo pode ser colocada em seu computador mudando para logaritmos.
A - (1 - d) n
log A = t log (1 - d)
Isso se assemelha à forma X Y - Z. Deixe a escala em X representando t, a escala em Y representando log (1 - d) e a escala em Z representando log A.
Nota: As escalas usadas no kit que tomamos como referência podem ser em alguns cálculos diferentes das usadas no nosso projeto. Adaptações podem ser feitas para se obter novas escalas com base nas figuras.
As escalas do computador original do kit.