Para o estudante ou mesmo para o profissional da eletrônica existem momentos em que se deseja calcular uma bobina, pois seu valor não é comercial e portanto ela não pode ser obtida pronta no mercado. Outro fator que pode exigir este cálculo é a necessidade de se ter rapidamente a bobina em mãos não havendo tempo para se sair para sua aquisição. Neste artigo mostramos como indutores de pequenos valores podem ser calculados.
A indutância, ou coeficiente de auto-indução, de uma bobina depende da maneira como ela é construída, ou seja do seu formato, número de espiras e eventual existência de um núcleo de material ferroso ou outro material que apresente propriedades magnéticas específicas.
Para um solenóide, bobina cilíndrica, a indutância é medida em Henry (H) e seus submúltiplos são utilizados, obtendo-se assim indutâncias em milihenry (mH) e microhenry (uH). Normalmente utiliza-se a letra L para representar a indutância de um indutor. Damos a seguir uma primeira fórmula para o cálculo de indutância, sendo a mesma válida para um solenóide ou bobina cilíndrica em que o comprimento do enrolamento não seja muito maior que o diâmetro. Na figura 1 temos as dimensões que serão levadas em conta nos cálculos.
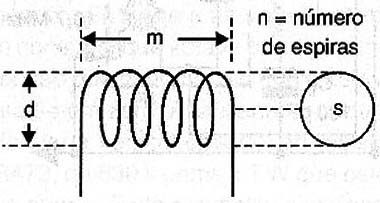
A fórmula será;
L = 1,257 x (n2 x S)/(108 x m)
Onde:
L = indutância em Henry (H)
N = número de espiras
S = área da secção transversal da figura em cm2
m = comprimento do enrolamento em cm
A área da seção transversal da bobina pode ser calculada facilmente a partir do seu diâmetro ou do raio (r) pela fórmula, conforme a figura 2 mostra:
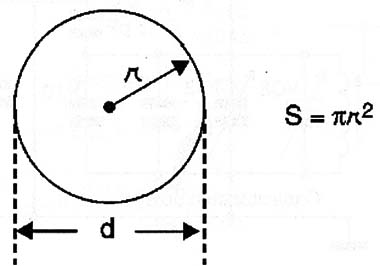
S = ? x r2
Onde:
S = área da secção transversal em centímetros quadrados
? = 3,14 (constante)
Exemplo de cálculo:
Qual é a indutância de um solenóide que é formado por 100 espiras de fio esmaltado numa forma de 2 cm de diâmetro, ocupando 3 cm de comprimento, conforme mostra a figura 3?
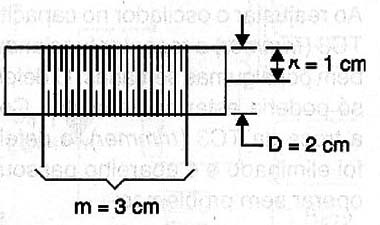
Solução:
Como não temos a área da secção transversal, precisamos calculá-la a partir do diâmetro da bobina usando a fórmula:
S = Π x r2
Como o diâmetro (D) é 2 cm, o raio (R) será 1 cm, portanto:
S = 3,14 x 1 = 3,14 cm2
Temos então:
S = 3,14 cm2
n = 100 espiras
m = 3 cm
Aplicando esses valores á fórmula temos:
L = 1,257 x [(100)2 x 3,14]/(108 x 3)
Elevando 100 ao quadrado:
L = (1,257 x 10 000 x 3,14)/(108 x 3)
Resolvendo:
L – (1,257 x 3,14)/3 x 104 /108
Chegamos a:
L = 1,315 x 10-4 ou 0,13 mH (130 µH)
Para o caso de bobinas que façam uso de núcleos, usamos a seguinte fórmula:
L = 1,257 x (n2 x S x β)/(108 x m)
Onde:
β = coeficiente de permeabilidade do material usado no núcleo (vácuo = 1)



















