Conforme vimos na lição anterior, a finalidade de um computador analógico é realizar operações matemáticas usando tensões (grandezas analógicas). Os computadores analógicos modernos se baseiam em amplificadores operacionais no entanto existem outros circuitos e até mesmo componentes que podem ser usados em cálculos envolvendo grandezas analógicas.
Por exemplo, os potenciômetros. Você sabia que potenciômetros podem fazer contas?
O que vamos fazer agora é entrar numa parte prática de nosso curso em que, para aprender como funciona um computador analógico vamos ensinar montar um usando potenciômetros.
Os leitores poderão aperfeiçoar este projeto e até incluir recursos mais modernos como o uso de amplificadores operacionais, em especial tipos que hoje são disponíveis e que permitem obter uma precisão maior de cálculo.
O potenciômetro fazendo contas
Se a ideia básica é representar quantidades por uma tensão, tudo o que precisamos, em primeiro lugar, é ter uma tensão padrão. Esta pode vir de uma bateria de tensão V1, conforme mostra a figura 1.
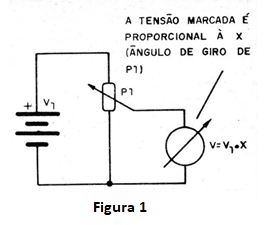
Se ligarmos um potenciômetro conforme mostra esta figura, a tensão que teremos entre seu cursor e o terminal negativo dependerá da sua posição ou giro.
Assim, podemos girar o eixo do potenciômetro de modo a representar qualquer quantidade entre 0 e V1. Supondo que V1 seja 1 volt, podemos dizer que este circuito representa qualquer quantidade de X entre 0 e 1. Ligando um indicador de tensão no cursor deste potenciômetro, ele marcará um valor proporcional ao ângulo que girarmos o eixo do potenciômetro.
Lembramos que o potenciômetro consiste numa resistência que pode mudar de valor pelo movimento de um cursor, conforme mostra a figura 2.
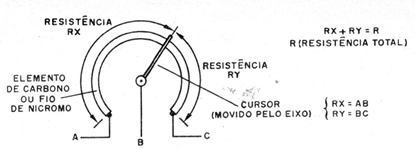
Dependendo da posição do cursor, a resistência entre A e B e entre B e C variam. Assim, o potenciômetro ligado da forma mostrada na figura 1 forma um divisor de tensão, ou seja, um circuito que divide a tensão da bateria de modo que ela fique entre 0 e 100% do máximo.
Mas, um potenciômetro sozinho não é suficiente para a realização de operações. Vamos supor que sejam ligados dois potenciômetros da maneira mostrada na figura 3.
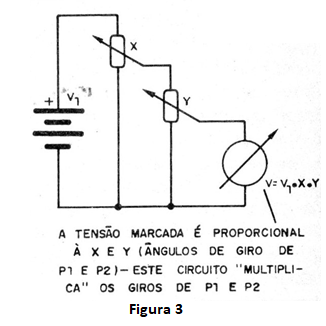
O cursor de X permite-nos pegar uma fração da tensão de entrada. Vamos supor que este potenciômetro esteja dotado de uma escala calibrada de 0 a 1. Isso significa que, movimentando o eixo deste potenciômetro, podemos “pegar" qualquer quantidade entre 0 e 1.
Pois bem, o segundo potenciômetro, marcado como Y, permite fazer a mesma coisa em relação a X, ou seja, podemos pegar qualquer fração entre 0 e 1, porém do que for retirado de X.
Se o cursor de X estiver em 0,5 e levarmos o cursor de Y a 0,6, o resultado que teremos será 0,5 de 0,6, ou seja, 0,5 x 0,6 = 0,30. Teremos então no final uma tensão que corresponde a 0,30 da tensão de entrada e teremos realizado uma multiplicação!
Dois potenciômetros ligados da maneira indicada multiplicam quantidades;
É claro que a partir da multiplicação podemos fazer outras operações, pois: dividir e multiplicar pelo inverso; elevar ao quadrado é multiplicar um número por ele mesmo, e assim por diante.
Mas, ainda existe um problema a ser resolvido:
O detector de nulo
Não é muito interessante ter um indicador de tensão para marcar o resultado da operação. Uma maneira mais interessante é também usar um potenciômetro com uma escala que tenha o resultado em algum ponto.
Assim, uma vez que tenhamos proposto o problema, basta girar o potenciômetro de resposta até que o resultado seja atingido. E claro que para isso é preciso haver algum tipo de indicador que avise quando este resultado for encontrado. Uma maneira simples de fazer isso é mostrada na figura 4.
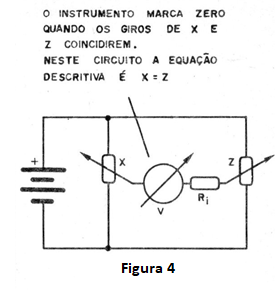
Se o potenciômetro X tiver seu cursor ajustado para uma certa posição que resulte numa tensão em V, girando o potenciômetro 2 vamos, em determinado momento, encontrar uma posição em que teremos a mesma tensão.
Deste modo, a tensão no instrumento se anula e isso ocorre para um único valor. Teremos ”zerado" o circuito encontrando a resposta. Num circuito de multiplicação, conforme mostra a figura 5, teremos então 3 potenciômetros.
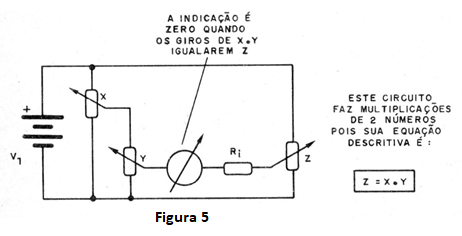
Os dois primeiros correspondem aos dados do problema, ou seja, os valores que devem ser multiplicados, divididos etc. O terceiro, marcado com Z, serve para zerar o instrumento, encontrando a resposta.
Assim, a operação se torna simples. Se quisermos multiplicar 0,5 por 0,6, ajustamos X em 0,5 do giro, Y em 0,6 do giro e depois vamos virando o eixo de 2 até que o instrumento indicador de nulo marque zero. Neste momento leremos na escala de Z o valor 0,30 com certeza!
Na figura 6 temos uma configuração com 4 potenciômetros, que permite trabalhar com três valores.
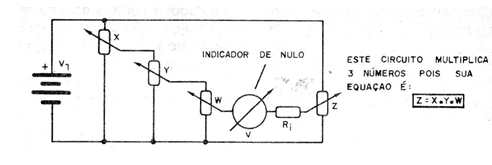
Veja que, se quisermos operar com dois números neste computador, bastará levar o potenciômetro X para 1, pois 1 multiplicado por alguma quantidade é igual a esta quantidade e simplesmente considerar Y vezes W!.
Que tipos de operações podem ser feitas?
Além das quatro operações, com 3 potenciômetros podemos fazer os seguintes tipos de cálculos:
- potenciação;
- radiciação;
- cálculo de senos e cossenos de ângulos;
- resolução de equações simples.
Podemos comparar este aparelho às réguas de cálculos, com a diferença de que em lugar de linguetas cursoras temos potenciômetros com. seus cursores, mas que chegam aos mesmos resultados.
Considerações sobre a precisão
Um problema importante que ocorre no projeto e operação deste tipo de computador é a introdução de erros. Quando trabalhamos com. circuitos digitais, a introdução de erros quase não ocorre, porque variações de tensão no circuito não afetam o resultado. Uma tensão que varie entre 3 e 5,5 V é interpretada como 1 por um circuito, do mesmo modo que uma tensão entre 0 e 0,7 V é interpretada seguramente como “0".
No caso de um computador analógico, as variações, por menores que sejam, afetam os resultados. Se quisermos representar a quantidade 3,1 e levarmos o cursor do potenciômetro para um pouco além ou um pouco antes desta posição na escala, teremos 3,2 ou 3,0 ou ainda qualquer valor intermediário, pois este tipo de máquina não reconhece quantidades discretas, ou seja, não trabalha só com valores inteiros!
Isso significa que a precisão dos componentes, principalmente a tolerância do potenciômetro e sua linearidade, são fatores que influem na realização prática de um projeto preciso.
Do mesmo modo, quando ligamos um potenciômetro à outro, conforme mostra a figura 7, um “carrega" o outro, no sentido de que passamos a ter no ramo inferior RX2 a ligação de uma resistência RY que altera o seu valor.
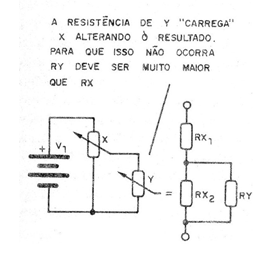
Para que isso não ocorra, RY deve ser muito maior que RX.
Quanto maior for RY em relação a RX, melhor é a precisão do computador, mas em compensação exige-se detectores de nulo mais precisos.
Em suma, a precisão deste computador é como a de uma régua: depende não só da sua qualidade, como também do manejo e da própria leitura.
Usando componentes comuns, comprados em lojas, pode-se ter uma precisão de 2 a 5%, o que não pode ser comparada à de uma calculadora (que chega a ser absoluta!), mas serve para ilustrar o funcionamento do circuito.
O mesmo ocorre em relação aos computadores analógicos que fazem uso de amplificadores operacionais. Os componentes do circuito não apresentam precisão absoluta. Resistores, por mais precisos que sejam, chegando em alguns casos a 0,1% somam suas imprecisões a medida que o sinal passa de etapa para etapa.
No entanto, é interessante observar que em muitos sistemas naturais que trabalham com sinais analógicos a imprecisão existe e é considerada natural. Não conseguimos diferenciar com precisão dois tons de frequências próximas, pois nosso sistema auditivo é analógico.
A natureza se adapta a operação com sinais analógicos sem ter problemas. É por esse motivo que pesquisadores que trabalham com biônica e inteligência artificial estão cada vez mais olhando com cuidado para a computação analógica em seus trabalhos.
Outros detectores de nulo
Nos exemplos que demos, usamos um instrumento para indicar o ponto em que a resposta era alcançada, isso porque trabalhamos com a tensão de uma pilha. No entanto, existem outras possibilidades de uso de detectores e até mesmo de fontes de tensão.
Por exemplo, pera tornar o circuito mais sensível, de modo a não afetar a precisão do resultado podemos ligar o instrumento a um amplificador transistorizado. Outra possibilidade, que leva a melhores resultados, é usar um amplificador operacional, conforme mostra a figura 8.
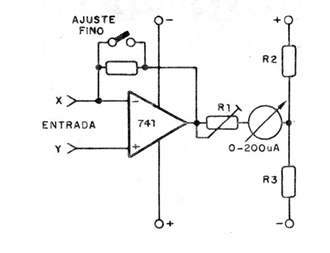
Neste caso, como a amplificação do operacional e muito grande, em lugar do instrumento podemos usar LEDs. O apagamento dos dois LEDs mostra o ponto de equilíbrio.
Na figura 9 temos um exemplo de um circuito de indicador de nulo que faz uso de LEDs em oposição.
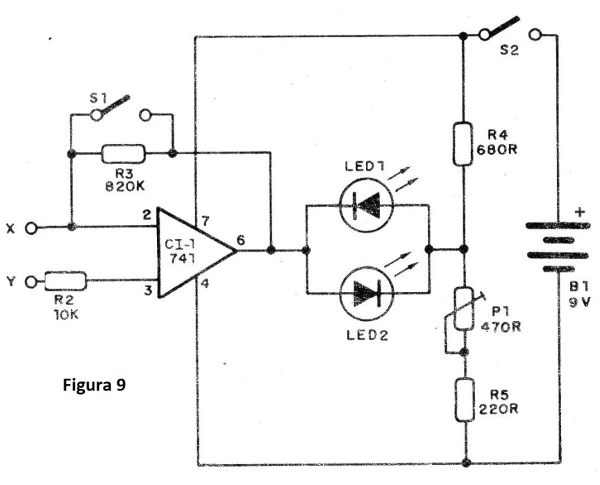
Neste circuito quando a tensão no pino 6 é maior que a metade da tensão de referência, ajustada em P1 e dada pelos resistores R4 e R5 acende o LED2. Quando ela é menor, acende o LED1.
Como o ganho do operacional depende da realimentação, podemos até colocar uma chave que permite aumentar o ganho à medida que nos aproximamos da solução do problema (ponto de equilíbrio) e com isso elevar a precisão.
Também podemos trabalhar com sinais de áudio em lugar de tensões continuas. Substituímos a pilha (ou bateria) por um oscilador de áudio e o detector de nulo passa a ser um fone de ouvido ou ainda um amplificador ligado a um alto-falante. (figura 10)
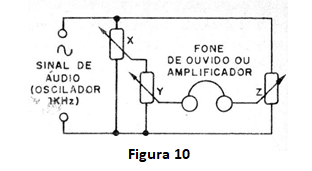
O fone de cristal é o ideal para este tipo de detecção, pela sua alta impedância.
Não precisamos dizer que a montagem de um computador analógico consiste numa excelente sugestão de trabalho escolar.
Antes da segunda guerra mundial, os Computadores Analógicos de grande porte ajudaram na elaboração de tabelas de tiros e de muitos trabalhos que hoje podem ser feitos até mesmo por pequenos computadores. Naquela época as escolas também tinham seus microcomputadores analógicos, como o que descrevemos, e que eram usados não só no ensino da matemática em si, como também na introdução da informática da maneira como ela tendia naqueles tempos.
Não queremos dizer que o computador analógico deva ser esquecido, pois sua importância didática é infinita. Muito pelo contrário, publicando artigos sobre este equipamento, esperamos que ele seja colocado no lugar que ainda lhe cabe: ensinar os jovens nas escolas.
Tipos de Potenciometros
Nos projetos de computadores analógicos e qualquer outro que faça uso de potenciômetros usamos normalmente os tipos de 270 graus que sempre.
No entanto eles não são únicos que podem ser obtidos atualmente. Além dos tipos deslizantes temos outros como o que descrevemos a seguir.
Você já precisou para uma aplicação de um potenciômetro “sem fim” ou “endless” que possa girar continuamente a rotação completa de 360 graus? Sim, este componente existe. É o potenciômetro Endless e a Piher os fabrica. Neste artigo tratamos um pouco deste componente que pode ser de grande utilidade num projeto de automação.
(*) Este artigo é baseado no datasheet do ST-15, potenciômetro Endless da Piher que pode ser adquirido na Mouser Electronics no link: https://www.mouser.com/new/piher/piher-st-15-rotation-potentiometers/ . O datasheet, por sua vez, pode ser acessado no link: https://www.mouser.com/datasheet/2/325/ST-15-1368214.pdf
Os potenciômetros comuns possuem um giro definido, normalmente chegando aos 270 graus, obtendo-se assim uma faixa de controle que não é total se levarmos em conta o giro possível do eixo, conforme mostra a figura 11.
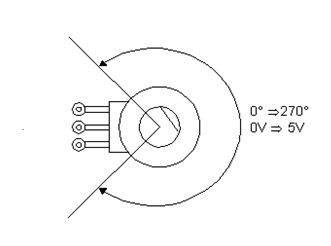
Em muitas aplicações que envolvam o uso do potenciômetro para o sensoriamento, este ângulo não é problema, mas pode ser que ocorra a necessidade de se obter um sensoriamento no giro completo e, mais que isso, que o potenciômetro possa ser livre dando voltas “sem parar”.
Para esta finalidade deve ser usado um potenciômetro com características especiais que é o chamado “endless” ou sem fim. A Phier, cujos componentes podem ser adquiridos na Mouser Electronics, disponibiliza uma linha de potenciômetros de 360 graus de 15 mm. A série ST-15 pode ser encontrada com valores de 1 k a 100 k na série de 1 – 2 – 2,2 – 2,5 – 47, e 5).
Na figura 12 temos os aspectos destes componentes.
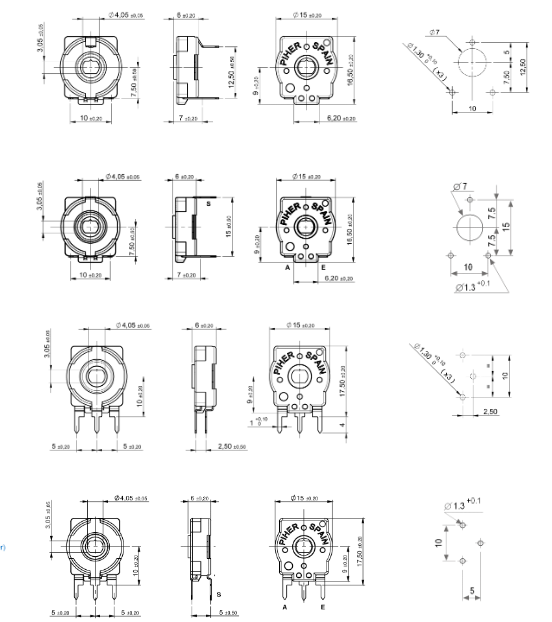
E para facilitar o uso numa aplicação o fabricante também disponibiliza prolongamentos, eixos e outros recursos mecânicos de acoplamento ao seu sistema, mostrados na figura 13.

Certamente estes potenciômetros podem servir de base para um projeto de computador analógico interessante.
Na terceira lição deste curso muito rápido vamos ensinar o leitor a montar um pequeno computador analógico didático experimental que funciona como uma régua de cálculo eletrônica.
A precisão dependerá da tolerância e qualidade dos potenciômetros usados e com imaginação o circuito pode ser ampliado para mais cálculos com a utilização de mais potenciômetros e de chaves comutadoras.
Índice
Introdução à Computação Analógica (CUR6000)
Computação Analógica – Lição 1 – Os Computadores Analógicos (CUR6001)
Computação Analógica – Lição 2 – Os Componentes do Computador Analógico (CUR6002)
Computação Analógica – Lição 3 – Monte um Computador Analógico (CUR6003)




















