Com a terminologia existente no campo da eletrônica é quase que impossível, a partir das siglas, ter uma noção, por pequena que seja, do componente ou produto eletrônico. A maioria das siglas, principalmente no Brasil, são provenientes de expressões do idioma inglês. Isto se deve, fundamentalmente, à grande infiltração deste idioma no nosso País, pois, uma parte dos componentes eletrônicos e folhas de especificações dos componentes são provenientes dos E.E.U.U.
Aquilino R. Leal
A reação em aceitar ou não as siglas "importadas" depende, basicamente, da riqueza do idioma onde são implantadas e do modo de discernir da população do País em questão. No nosso caso não só aceitamos todas as siglas como também incorporamos expressões e até frases completas na nossa língua (no duplo sentido!). É lastimável, por um lado, tal procedimento pois, afinal de contas, o idioma português é dos mais ricos na face da Terra, por outro lado isto é bom, pois para cada campo da ciência (no caso, a eletrônica) existe um vocabulário específico que não traz ambiguidade de sentido dos termos empregados usualmente num "diálogo técnico". Um exemplo do que acabamos de dizer é
a expressão "lay out" que até hoje, pelo menos eu, não tenho encontrado um termo de expressão tipicamente português capaz de, realmente, traduzir o que entendemos por "lay out".
É interessante observar como numa reunião de pessoas técnicas é difícil fazer-se entender; cada profissão ou ramo da ciência tem uma forma bem específica de se comunicar; esta forma de comunicação só é inteligível àqueles que exercem esta profissão específica. É o caso, por exemplo, da sigla PCM que só diz algo aqueles que lidam com a eletrônica ou telecomunicações: a um técnico nestes campos teremos dito que se trata de uma modulação ou código de pulsos (MCP), isto se o técnico falar português (ou inglês!); para o caso de um técnico espanhol, por exemplo, em eletrônica, também não teremos dito absolutamente nada! É porque a língua castelhana (ou serão os espanhóis?) "espanhola" tudo o que vier "na reta"! No caso, ele usará a sigla MIC ("Modulación por Impulsos Codificados") que a sigla da frase inglesa "Pulse Code Modulation" já traduzida para o castelhano.
A intenção aqui não é a de "traduzir" todas as siglas nem tampouco fornecer o seu significado pois isto é uma tarefa árdua senão impossível; a intenção é a de apresentar ao leitor algumas características funcionais de um VDR.
— ???!!
É.... assim não dá! Temos aí mais uma sigla! VDR é a sigla proveniente da expressão "Voltage Dependent Resistor". Certo?
- ???!!
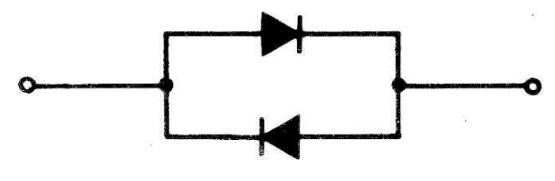
Bem... isto significa: Resistência Dependente da Tensão (R DT7!). Entende-se por tal, um componente cuja resistência diminuí ao aumentar-se a tensão — este componente é denominado "varistor", expressão esta procedente, igualmente, do inglês (como não poderia deixar de ser I), da contração das palavras "VARiable resISTOR" (resistor variável); no entanto, sob a denominação varistor se compreendem também outras resistências não ôhmicas (resistências que não obedecem a lei de Ohm) como, por exemplo, as resistências NTC, PTC e LDRs.
- ????!!
Meu caro...resistências de siglas de expressões "importadas"!
resistências NTC: "Negative Temperature Coefficient" ou: resistências com coeficiente de temperatura negativo (RCNT?),
resistências PTC: "Positive Temperature Coefficient" ou: resistências com coeficiente de temperatura positivo (RCPT?);
resistências LDR: "Light Dependent Resistor ou: resistências dependentes da luz (RDL?).
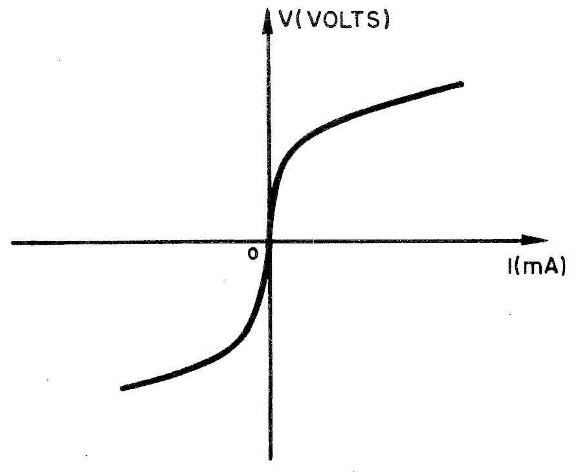
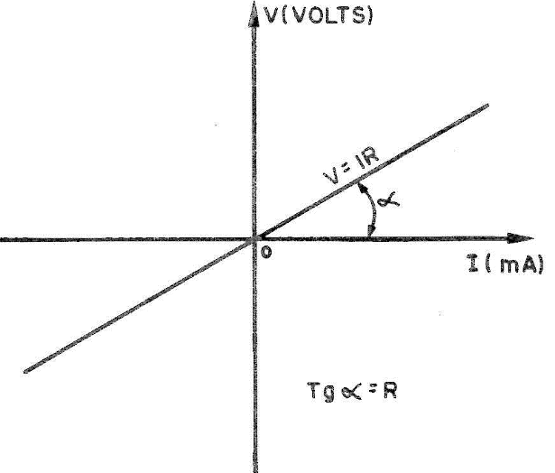
O VDR é, portanto, um resistor cuja resistência varia com a tensão aplicada entre seus terminais. A característica típica "tensão versus corrente" de um VDR convencional é mostrada na figura 1, observar que esta curva se assemelha à que se obteria pela conexão de diodos em antiparalelo (figura 2). Notar a não linearidade entre V (tensão) e I (corrente) como ocorre nos resistores convencionais aos quais podemos aplicar a conhecida lei de Ohm: V = I.R que, corresponde, graficamente, à reta mostrada na figura 3.
A relação entre tensão e corrente de um VDR (figura 1) pode ser expressa por intermédio de uma fórmula bastante simples, ou seja:
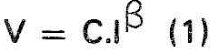
em que:
C é uma constante construtiva que depende fundamentalmente da seção e do comprimento do elemento VDR,
ß é uma constante do material que caracteriza o aumento de tensão em relação com o crescimento da corrente.
Para os VDRs práticos, os valores de C se encontram entre 100 e 1000 enquanto os de ß entre 0,17 e 0,25. Observar que os números C e ß são coeficientes adimensionais aos quais não corresponde nenhuma unidade. E em verdade a expressão (1) não é certamente a mais correta pois não expressa convenientemente as unidades de V e de i, o certo, matematicamente, seria:

e, desta forma, realmente, C e podem ser considerados adimensionais.
Em relação às expressões (1) e (2), se ß = 1, C representa uma resistência e se verificará a linearidade entre Ve I, o que caracteriza a lei de Ohm - figura 3.
A expressão (2) pode ainda ser escrita como:
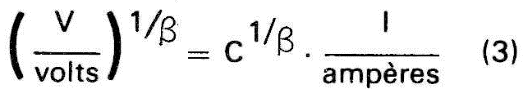
Pois bem, consideremos, por exemplo os seguintes valores:
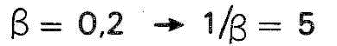
e
C = 100
que, aplicados em (3), nos fornece:
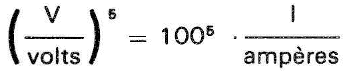
isto significa que quando cresce o valor da tensão no VDR, o valor da corrente que a percorre aumentará com a quinta potência da tensão, para os valores de ß e C fornecidos no exemplo. A figura 4 mostra a característica V versus I do VDR para estes valores; de imediato podemos observar pela análise desta figura que a região correspondente aos valores de I compreendidos entre, aproximadamente, 0 e 0,70mA, não apresenta um bom grau de precisão; para contornar o problema, como veremos adiante, poderíamos usar escalas logarítmicas em vez da escala linear empregada na figura 4.
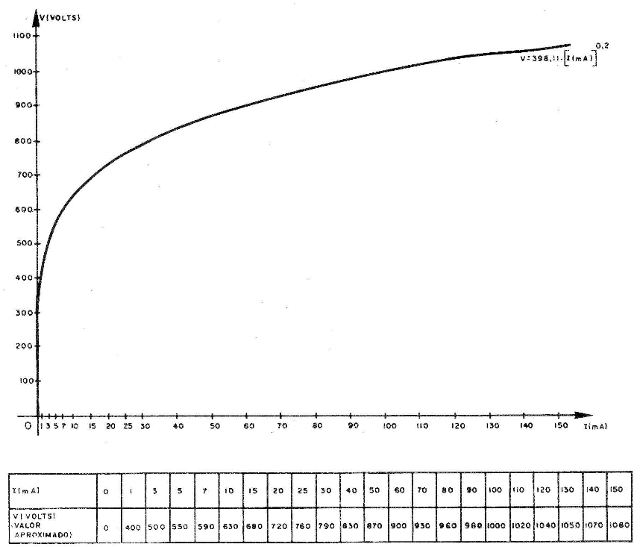
Bem... por ora chega de matemática! Em realidade, não teremos de preocuparmos com estes cálculos, pois as folhas de características dos VDRs, fornecidas pelo fabricante contornam este problema não nós fornecendo uma expressão matemática como as apresentadas acima, e sim, uma família de curvas como a mostrada na figura 5; isto facilita enormemente o nosso trabalho de escolher este ou aquele VDR dentro os fornecidos pelo fabricante.
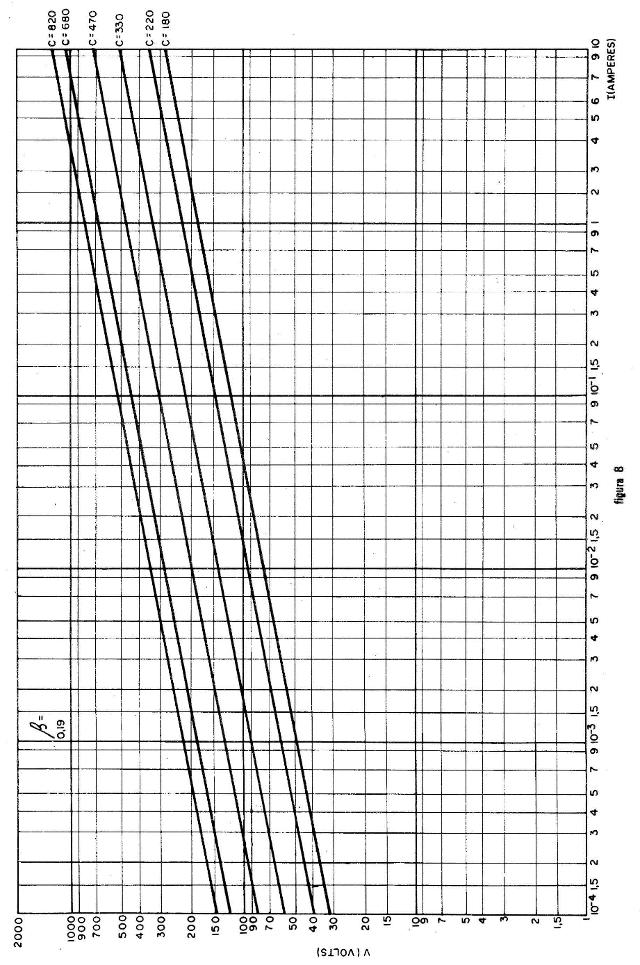
A figura 5 mostra as características tensão versus corrente para alguns valores usuais: ß= 0,19 e C = 820, 680, 470, 330, 220 e 180.
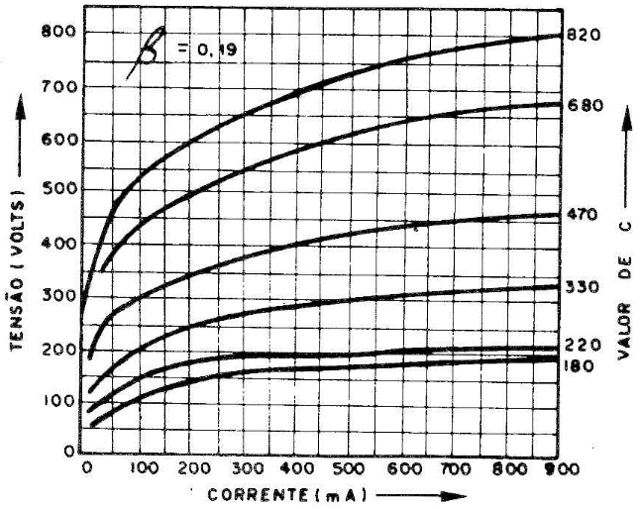
Da figura se verifica imediatamente que ao aumentar a tensão, a corrente cresce pouco de início e, para baixas tensões, o VDR apresenta valores elevados de resistência; ao aumentar-se gradativamente a tensão, a corrente vai tornando-se maior, porém mais rapidamente, que a tensão, ou seja: para grandes valores de tensão a resistência diminui velozmente.
Para melhor observar este fenômeno, ampliamos a curva superior da família de curvas da figura 5, conforme é mostrado na figura 6. IC= 820 e ß = 0,19). A equação desta curva pode ser deduzida a partir de (2) ou seja:
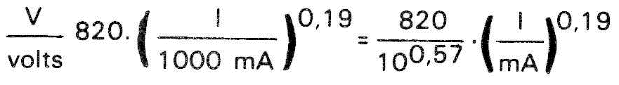
ou
V 221.I 0,19 com: V em volts e I em miliampères.
Para os pontos A, 8, C, D, E, F e G assinalados na figura 6 temos os seguintes valores de V e I extraídos do gráfico, bem como o cálculo da resistência do VDR em cada um desses seis pontos:
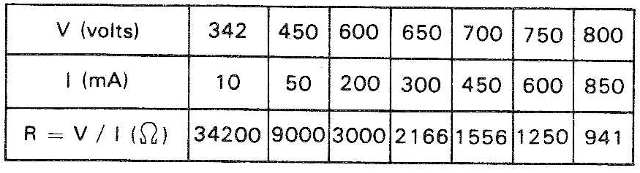
Os valores calculados para R denominam-se valores de resistência com/ corrente contínua (ou resistência estática) e somente são válidas com a condição de que se aplique uma tensão contínua V ao VDR e que desta tensão circule uma corrente contínua I. A resistência c.c. calculada acima só encontra aplicação secundária. Em primeiro lugar deveremos considerar a "resistência com oscilação- ou resistência c.a. como normalmente é conhecida. Para esclarecer este conceito faremos uso de um exemplo numérico: se a tensão no VDR (figura 6) oscila entre 700 e 750 volts, a isto corresponde uma variação na intensidade de corrente de 450 a 600 mA (vide tabela acima), assim:
variação de tensão = ?V:(750 — 700I=50 volts,
variação de corrente = ?l:(600 — 450I = 150mA daí vem:
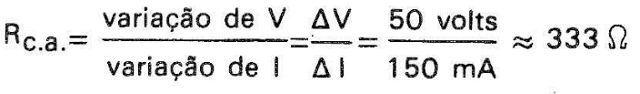
Isto quer dizer que o valor da resistência com oscilação depende não somente do valor médio da tensão em torno do qual se verifica a oscilação senão também da amplitude desta oscilação; verifiquemos isto para as oscilações em torno de um valor médio igual a 600 volts (ponto C da figura 6); estabeleçamos uma nova tabela cujos valores de I são extraídos da curva apresentada na figura 6.

De modo que, para o valor médio da tensão em 600 volts, se obtém todos estes valores de Rc.a. Seria muito mais conveniente que para um valor médio de tensão (ou intensidade) correspondesse um único valor para a resistência Rc.a.
Isto pode conseguir-se desde que tomemos uma oscilação pequena; se esta é infinitamente pequena não intervém em nada para a curvatura da característica e saberá do nosso interesse a inclinação do tangente à curva no ponto médio considerado.
Para mostra isto claramente, reportemo-nos ao exemplo procedente, V - 600 volts — ponto C da figura 6, e tracemos a tangente t no ponto em questão. Determinando a tangente trigonométrica do ângulo que esta tangente geométrica t forma com o eixo I, teremos o valor de Rc.a. para pequenas excursões (oscilações) de N: de acordo com a figura 6:
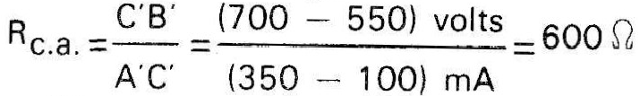
Observar que este valor não está mui -to longe do obtido anteriormente para a excursão de V compreendida entre 580 a 620 volts (última coluna da tabela acima), quando a excursão aumenta, o valor de Rc.a. vai tornando-se substancialmente diferente dos 600 encontrados pela inclinação da tangente no ponto considerado. A resistência c.a. determinada por este último método que foi designada por R c.a. é denominada resistência diferencial (1).
Como já tínhamos dito, a família de curvas características apresentada na figura 5, não é comum na folha de dados, mas, são fornecidas pelo fabricante nas denominadas escalas logarítmicas conforme ilustra a figura 7 — o papel assim quadriculado recebe o nome de papel log-log.
— ??? I

Uma escala logarítmica apresenta a propriedade de que a um mesmo fator lhe correspondem iguais distâncias, ou seja, por exemplo, a distância para o fator 10 é sempre a mesma, seja ela a distância entre 1 e 10 ou entre 10 e 100 ou, ainda, entre 100 e 1000; com o fator 2, são iguais as distâncias entre 1 e 2, entre 2 e 4, entre 3, 6 e 7, 2; entre 10 e 20, etc. Esta propriedade da escala logarítmica permite, numa mesma figura, cobrir em vasta amplitude de valores numéricos, de forma que os números do princípio da escala podem ler-se com igual facilidade que no final da mesma. A figura 7 mostra uma escala logarítmica que abrange três unidades logarítmicas, em toda a sua extensão podem ser indicadas formas de valores compreendidos entre 1 a 1000 (100 a 103) , entre 0,1 a 100 (10-1 a 102), entre 10 e 10000 (10-1 a 104) ou qualquer outra forma de valores compreendida entre 10m e 10 m+3 onde m é um número qualquer, positivo, negativo ou nulo, conforme está indicado.
Com este procedimento a família de curvas da figura 5 torna o aspecto mostrado na figura 8; observar que realmente não se trata de curvas e sim de retas, aliás isto é uma característica dos logaritmos quando os mesmos são aplicados a equações do tipo apresentado nas expressões (1), (2) ou (3) — (2). A precisão da leitura dos valores neste tipo de apresentação é muito maior que a da figura 5; por outro lado, enquanto o primeiro gráfico compreendia os valores de 1 entre 0 e 900mA e de 0 a 850 volts para V, este último ampliou a forma para 10-4 a 10 ampères e de 1 a 200 volts, respectivamente, ocupando, praticamente a mesma área!
Os inconvenientes desta representação são os seguintes: não existe o ponto zero;
— a leitura dos valores numéricos exige muita atenção e alguma prática—os valores de resistência diferencial não são tão imediatamente extraídos como no caso da escala linear, entre outros mais ou menos importantes.
(1) A resistência diferencial nada mais é do que o valor da derivada dV/dl no ponto I considerado.
Para o caso em pauta temos:

valor este não está mui longe do calculado por um método aproximado.
(2) Isto pode ser imediatamente verificado a partir da expressão geral V = C.lß quando aplicamos o operador logarítmico a ambos membros da igualdade, ou seja:
log V = log C + ß.log I, designando:
Y = log V
log C = n (constante) e
log I = X
vem:
Y = ßX + n que é a equação de uma reta.