As ondas de rádio ou ondas eletromagnéticas são a base de muitos meios de comunicação eletrônica. Como são produzidas estas ondas e que componentes usados em seus circuitos é o assunto artigo de grande interesse para todos que estudam eletrônica.
Urna carga elétrica parada produz um campo elétrico cuja intensidade em qualquer ponto do espaço pode ser calculada pela fórmula:
E = k.Q/d2 onde:
E é a intensidade do campo em N/C
K é uma constante que equivale a 9 x 109 N – m2/C2
Q é a carga que produz o campo em
d é a distância em metros.
Por outro lado, uma carga elétrica em movimento produz um campo magnético vetor indução magnética B pode ser calculado pela seguinte fórmula:
B = (U0.01/ (2.3, 14.r) )
onde:
B é a indução magnética dada em T Tesla)
U0 é a permeabilidade magnética do vácuo e vale 4.3, 14.10-7
i é a intensidade da corrente que corresponde ao movimento da carga em ampères.
r é a distância considerada em metros
Pois bem, o que acontece se uma carga entrar num movimento oscilatório, ou seja, indo e vindo num condutor?
Durante o movimento de ida e vinda, o movimento é responsável pela criação de um campo magnético, mas durante os breves instantes em que a carga para inverter seu sentido de movimento é criado um campo elétrico.
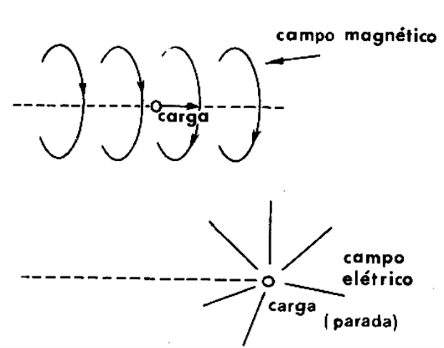
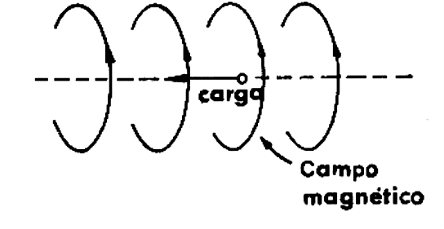
O resultado disso é que a energia empregada neste processo é convertida e irradiada na forma de ondas eletromagnéticas, ou seja, que correspondem a alternância do campo elétrico com o magnético. Estas são as ondas de rádio que se propagam no vácuo a uma velocidade de 300 000 quilômetros por segundo.
A velocidade com que a movimentação das cargas ocorre determina a frequência da emissão, a qual é medida em Hertz (Hz).
Nas telecomunicações são usadas as ondas de rádio que se situam em frequências entre 10 000 Hz (10 kHz) e mais de 1 GHz (1 000 000 000 Hz).
Fora desta faixa ainda temos ondas eletromagnéticas, mas sua utilidade será analisada em outra ocasião.
O circuito LC
A maneira mais simples de se produzir ondas de rádio é através do denominado "circuito oscilante" em que temos uma bobina (L) e um capacitor (C), ligados conforme mostra a figura 2.
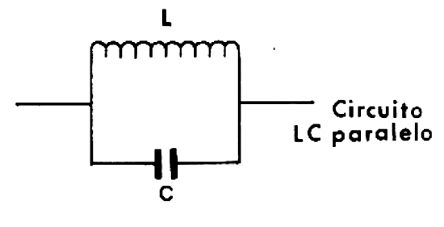
O capacitor é um componente que funciona baseado em cargas estáticas, ou seja, as cargas armazenadas nas suas armaduras são mantidas por um campo elétrico entre elas. Já o indutor é um componente que funciona baseado em campo magnético, pois a corrente que circula através de suas espirais produz um campo magnético, o qual armazena energia.
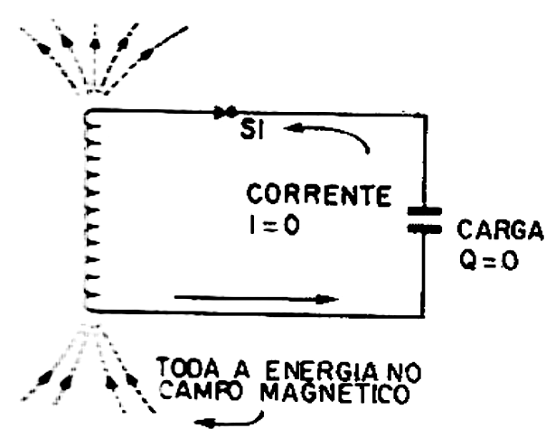
Para entender como funciona o circuito oscilante, vamos partir de uma situação inicial em que existe um capacitor carregado, conforme mostra a figura 3 e uma chave S.
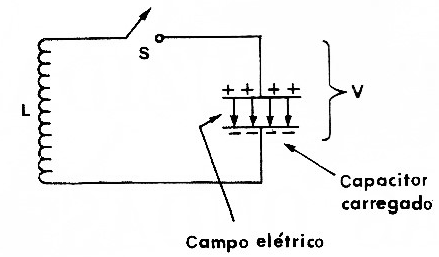
Na situação inicial, toda a energia do sistema está armazenada no campo elétrico entre as armaduras do capacitor. As cargas estão paradas não havendo qualquer circulação de corrente e a tensão entre as armaduras é máxima.
Quando a chave é fechada a corrente começa a fluir pelo Indutor, cuja resistência ôhmica supomos ser desprezível.
Nestas condições, conforme mostra a figura 4, a tensão entre as placas do capacitor cai e ao mesmo tempo a corrente no indutor aumenta produzindo um forte campo magnético que passa a armazenar toda a energia do-sistema.
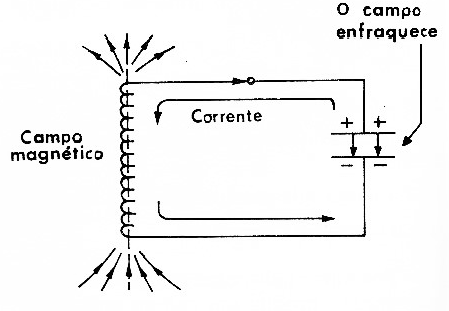
Quando a carga do capacitor se reduz a zero, e a corrente cessa, toda a energia do sistema se encontra no campo magnético cujas linhas de força se estendem até e infinito. Neste instante, as linhas do campo começam a se contrair, pois ele não pode ser mantido neste estado. Nesta contração é induzida no indutor uma corrente que passa a fluir em direção às placas do capacitor, mas tendendo a carregá-lo com polaridade oposta à da situação inicial.
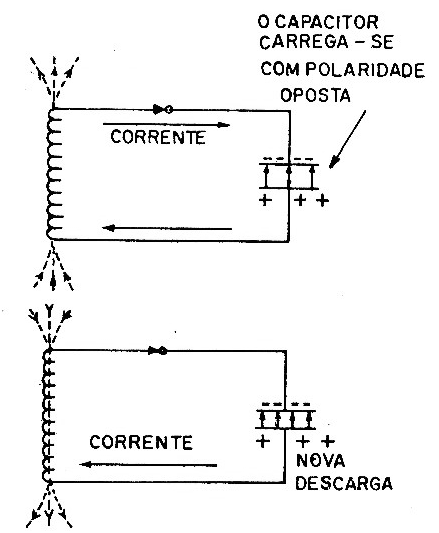
A corrente flui para o capacitor até que suas placas atingem o mesmo valor de tensão inicial, mas com polaridade oposta e o campo magnético no indutor se reduz a zero.
A energia que estava no campo magnético novamente volta para a forma de um campo elétrico.
Entretanto, esta situação também é transitória. Um novo ciclo de descarga se no capacitor que agora faz circular em sentido contrário uma corrente pelo indutor.
O ciclo permaneceria indefinidamente se não houvesse qualquer perda ou irradiação de energia pelo sistema.
Se ligarmos uma antena a este circuito, conforme mostra a figura 7, ondas eletromagnéticas serão produzidas e irradiadas pelo espaço.
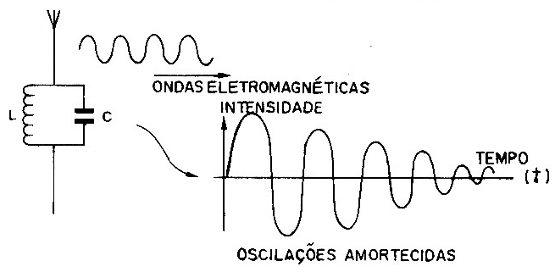
A oscilação que ocorre vai então reduzindo sua intensidade gradativamente até zero, à medida que a energia vai sendo perdida ou irradiada para o espaço.
Circuitos eletrônicos
Para que as oscilações possam ser mantidas, à medida que a energia se perde ou é irradiada, é preciso haver uma reposição constante, o que é conseguido através de circuitos eletrônicos.
Assim, no circuito da figura 8, já muito conhecido dos leitores, a bobina e o capacitor determinam a frequência das oscilações, ou seja, formam o "circuito ressonante” ao mesmo tempo em que o transistor "repõe" constantemente a energia que mantém as oscilações.
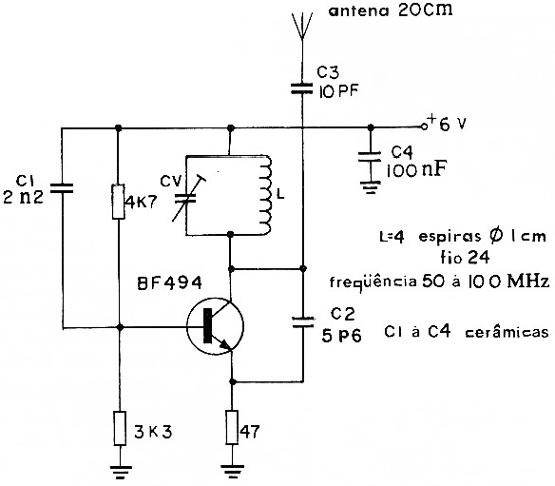
A antena é responsável pela irradiação da energia através do espaço na forma de ondas eletromagnéticas. A energia que o transistor repõe é obtida de uma fonte de alimentação como por exemplo pilhas ou a própria rede local.
Cálculos
Um circuito LC não pode operar em qualquer frequência. A velocidade com que se alternam as trocas de campos elétricos para magnéticos é determinada pelos valores do capacitor e do indutor.
Pela lei da Conservação da energia, aplicada ao capacitor e ao indutor, deve ser satisfeita a seguinte equação:
W = Q2/2.0 LI2/2 = constante
Derivando esta equação em relação ao tempo temos:
dW/dt = Q/C.dQ/dt L.I dI/dt = 0 (2)
O decréscimo da corrente nas placas de um capacitor é dado por:
I = dI/dt (3)
Podemos então simplificar a equação (2) escrevendo:
Q/C + L dI/dt = 0 (4)
Esta condição só pode ser satisfeita se oscilações puderem ocorrer: Assim, podemos escrever:
L. dI/dt = -1/C.Q (5)
Assumindo que, com o capacitor carregado temos:
Q = Qo cos wt (6)
temos: I = - Qo w senwt (7)
Substituindo na equação diferencial (4) temos:
- L.Qo.w2 cos wt = I/C . Qo cos wt
Simplificando:
L.w2 = I/C
ou
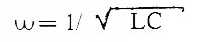
A grandeza w equivale a 2.π i. f e é chamada pulsação onde f é a frequência. Escrevemos então que:
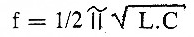
Esta fórmula nos permite calcular a frequência de ressonância de um circuito LC onde C é dado em farads, L em henrys e f, a frequência, é obtida em Hertz.




















