Este artigo visa a elaboração de um algoritmo, utilizando o software MatLab, capaz de modelar o comportamento de um veículo autônomo inteligente quando este é inserido em um labirinto qualquer.
Nota: Artigo publicado na revista Eletrônica Total 158 de 2013.
Neste projeto, o robô deverá encontrar todos os possíveis caminhos a serem percorridos no labirinto antes de conseguir finalmente a trajetória correta para sua saída. Serão gravados os caminhos e ao final, todos os lugares percorridos serão conhecidos. Para realizar as simulações foram utilizadas matrizes que representam os labirintos a serem percorridos. Ao fim da execução do algoritmo, as coordenadas dos caminhos percorridos pelo robô são informadas, e uma ilustração gráfica mostrará esses caminhos de forma mais clara. Após isso, a matriz que foi modificada será modelada em Redes de Petri, ferramenta utilizada para modelar e analisar sistemas.
Vários estudos são desenvolvidos com robôs nos dias de hoje e pouco se sabe sobre a origem dessa palavra. Ao contrário do que muitos possam imaginar, a primeira pessoa que utilizou a palavra "robô" foi um escritor de peça teatral chamado Karel Capek. Ele a usou quando escreveu sua peça R.U.R. (Rossum's Universal Robots), em 1921. O espetáculo possuía dispositivos mecânicos com aparência humana como personagens, que não apresentavam qualquer tipo de sensibilidade, realizando tarefas rotineiras de forma automática.
Existem algumas atividades, nesse mundo de descobertas, que são de difícil acesso ao ser humano, isso quando não se fala na impossibilidade da intervenção direta do homem. Um exemplo típico são as perfurações de petróleo feitas em profundezas cada vez maiores, onde é impossível um ser humano chegar e tentar qualquer ação. Outro exemplo são as investidas do homem em outros planetas, cada vez mais frequentes. São ambientes totalmente desconhecidos dos quais ainda se procura obter características ambientais, tornando inviável uma ação mais direta.
No que se refere à evolução dos robôs, existe uma classificação quanto ao seu surgimento. Esta pode ser dividida da seguinte forma.
• Primeira Geração: Robôs Sequenciais - são controlados em malha aberta, têm dois a quatro graus de liberdade e executam apenas tarefas simples como as de carga e descarga de prensas e máquinas ferramenta.
• Segunda Geração: Robôs a Ciclos Programáveis - são um pouco mais sofisticados e possuem de quatro a oito graus de liberdade.
• Terceira Geração: Robôs Inteligentes - são capazes de se adaptar às modificações do ambiente mediante sistemas de controle, percepção, comunicação e decisão.
Aqui é abordada a modelagem de um robô que se comporta como um sistema a eventos discretos. Dessa forma, são considerados quatro sensores capazes de detectar um caminho livre ou fechado, disparando uma transição quando encontrado um caminho livre. O disparo da transição define que um passo deve ser realizado. Esse passo é entendido como um evento discreto, o que caracteriza um sistema a eventos discretos.
Teoria de sistemas a eventos discretos
Um Sistema a Eventos Discretos pode ser classificado como dinâmico, invariante no tempo, não linear, com espaço de estados discreto e dirigido por eventos. O SED tem seu estado alterado em instantes discretos no tempo. Quando se fala da modelagem desse tipo de sistemas, se possível identificar um conjunto de eventos no qual cada evento possa causar uma transição de estado, a variável "tempo" não pode ser considerada uma variável independente.
Um SED é considerado dinâmico, pois sua saída em qualquer instante t depende de valores passados da entrada. Em sistemas invariantes no tempo, se sua função de entrada é aplicada ao sistema unidades de tempo depois de t, a função de saída deve ser igual à obtida em t, deslocada de unidades de tempo. A não linearidade dos sistemas está associada com a não validade do princípio da superposição. Quando se fala em sistemas com espaço de estados discretos, tem-se que as variáveis de estado pertencem a um conjunto discreto podendo ter variáveis com valores simbólicos, por exemplo, alto e baixo. E finalmente para um sistema dirigido por eventos, estes ocorrem de forma assíncrona no tempo, ou seja, a ocorrência é independente do tempo.
A principal diferença entre um sistema a eventos discretos e outro a eventos contínuos está no modo de interação com o ambiente no qual tal sistema está inserido. Para o primeiro caso, os eventos gerados no ambiente provocam alterações na sua configuração interna determinando sua evolução dinâmica. Para os sistemas a eventos contínuos as modificações de estado são provocadas da troca de energia com o ambiente.
Um sistema a eventos discretos pode ser definido por três características básicas. São elas:
• Ciclo de funcionamento descrito através do encadeamento de eventos, que determinam as tarefas realizadas ou em realização;
• Ocorrência de eventos simultâneos, ou seja, diversos eventos podem ocorrer no mesmo período de tempo para modificar o estado do sistema;
• Necessidade de sincronização, uma vez que para se ter uma evolução dinâmica correta, o início de algumas atividades requer o término de outras.
Um SED pode ser definido como um sistema cuja evolução dinâmica depende da ocorrência de eventos. Um evento pode ter um caráter proposital, espontâneo ou pode ser um resultado da verificação de uma condição. Os eventos são responsáveis pela modificação de um estado presente em um estado futuro.
Um evento discreto pode ser considerado instantâneo, pois seu tempo de duração é desprezível para o sistema em geral. Um caso que pode exemplificar bem o que foi dito anteriormente, é o simples acionamento de uma lâmpada. O intervalo de tempo que a lâmpada leva para ser acesa entre o acionamento do interruptor e o momento em que a mesma foi finalmente ligada, é totalmente desprezível para o sistema em si.
Como exemplos de SEDs pode-se citar sistemas de manufaturas, sistemas de computação, sistemas de comunicação, sistemas de tráfegos, sistemas robóticos, entre outros diversos.
Teoria de Redes de Petri
"Redes de Petri" foi um modelo criado a partir da tese de doutorado de um alemão chamado Carl Adam Petri, a qual foi intitulada Kommunication mit Automaten (Comunicação com Autômatos) e apresentada na Universidade de Bonn em 1962. Tal modelo fora criado com o objetivo de modelar sistemas com componentes concorrentes.
As Redes de Petri são consideradas uma importante ferramenta matemática e gráfica na análise de diversos tipos de sistemas, inclusive em sistemas a eventos discretos, pois torna fácil a visualização do modelo de uma forma geral e o estado deste em qualquer instante de tempo.
Utilizando-se as Redes de Petri em modelagem de SEDs são observadas diversas vantagens em relação a outros modelos, dentre as quais algumas são listadas a seguir:
• Simplicidade na modelagem das principais características do sistema, por exemplo, concorrência, sincronismo e assincronismo, conflito, exclusão mútua, relações de precedência, não determinismo e bloqueio.
• Ótima visualização de dependência de sistemas. Focalização na informação local.
• Abordagem de modelagem do tipo refinamento e do tipo composição modular.
• Possibilidade de gerar código de controle supervisório diretamente de sua representação gráfica.
• Possibilidade de testar propriedades indesejáveis para os sistemas, tais como bloqueio e reinicialização.
• Análise de desempenho sem simulação é possível para muitos sistemas, desde que taxas de produção, utilização de recursos, segurança e desempenho possam ser avaliadas.
• Simulação de eventos discretos diretamente a partir do modelo e informação do estado atual do sistema que permite monitoração em tempo real.
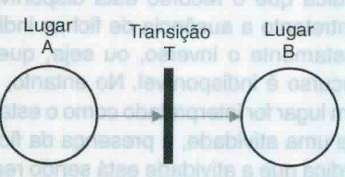
A Rede de Petri, ferramenta utilizada para modelar e analisar sistemas que apresentam concorrências e conflitos em sua dinâmica, é representada graficamente por grafos direcionados, bipartidos e ponderados com uma marcação inicial. A característica denominada de bipartidos faz alusão aos seus dois tipos de nós, que são denominados de lugar e transição. Os lugares são utilizados para modelar os componentes passivos do sistema, assim correspondendo às variáveis de estado. As transições são usadas para modelar os componentes ativos do sistema, ou seja, são os eventos que levam o sistema de um estado a outro. Os arcos sempre serão direcionados de um lugar para uma transição, ou de uma transição para um lugar. Na figura 1 pode-se observar os elementos de uma Rede de Petri, que foram descritos no parágrafo anterior. Assim, pode-se perceber que um arco parte do Lugar A para a Transição T e outro arco parte da Transição T para o Lugar B.
Em se tratando de representação gráfica, os círculos representam um lugar e as transições são representadas por uma barra ou um retângulo. Cada arco tem um peso discriminado pela letra k, que representa o número de arcos paralelos que ligam dois nós. A marcação de uma Rede de Petri atribui um número não negativo m, que são denominadas fichas. Essas fichas são representadas graficamente por círculos pretos. Essa marcação é um vetor M = [m1, m2, m3,..., mk]T, onde k é o número de lugares da rede, e mi o número de fichas do lugar i.
O estado do sistema é dado pela divisão das fichas nos lugares da Rede de Petri, sendo que cada lugar representa um estado parcial do sistema. Cada evento ocorrido no sistema está associado a uma transição. A ocorrência de um evento é representada pelo disparo da transição ao qual este está associado. O disparo de uma transição consiste na retirada de fichas dos lugares de entrada, indicando que esta condição não é mais válida após a ocorrência de um evento, e em seguida depositar fichas lugares de saída, indicando que estas atividades estarão, após o evento, sendo executadas.
Uma Rede de Petri é uma sêxtupla RP = (P, T, Ar, K, W, M0), onde:
• P = {p1, p2, pm} é um conjunto finito de lugares;
• T = {t1, t2, t3,..., tn} é um conjunto finito de transições;
• Ar í (P X T) u (T X P)
• K: P —> N u {ꝏ} é a função de capacidade;
• W: Ar —> N+ é a função de ponderação;
• Mo: P —> N é a função de marcação inicial, que satisfaz V p E P: Mo(P) ≤ K(P)
Levando em conta que em um sistema se deseja estudar somente o comportamento lógico, e ainda este apresenta alterações de estados definidos por transições discretas, pode-se utilizar uma metodologia para realizar a modelagem deste sistema. Essa metodologia de modelagem define que cada evento físico do sistema que resulta em uma mudança de estado é representado por uma transição na Rede de Petri. Assim, os estados do sistema são representados pela marcação da rede e os lugares são as partes que formam o sistema.
Com isso, tem-se que um lugar pode ser compreendido como o estado de um recurso ou de uma atividade. Se um lugar for interpretado como sendo o estado de um recurso, o número inicial de fichas pode ser constante para representar que existe uma quantidade fixa de recursos no sistema ou variável para representar o número de tarefas realizadas no sistema. Sendo um lugar entendido como o estado de um recurso, a presença mínima de uma ficha nesse lugar indica que o recurso está disponível, entretanto a ausência de fichas indica justamente o inverso, ou seja, que o recurso é indisponível. No entanto, se um lugar for interpretado como o estado de uma atividade, a presença da ficha indica que a atividade está sendo realizada e a ausência de fichas indica que a atividade não está sendo realizada.
Por fim, uma transição pode ser entendida como o início de um processo ou uma atividade, e também como seu término. Tendo o conhecimento desses conceitos, pode-se modelar um sistema qualquer em Rede de Petri seguindo alguns passos, que serão listados a seguir:
1. Identificar todos os recursos e atividade suficientes para se ter o funcionamento do sistema em questão;
2. Determinar uma ordem de ocorrências das atividades de acordo com as relações de precedência definidas na descrição do funcionamento do sistema;
3. Para cada atividade determinada no tópico anterior deve-se:
• Criar e etiquetar um lugar para representar a condição da atividade;
• Criar uma transição para representar o início da atividade com arcos direcionados para os lugares de saída;
• Criar uma transição que represente o término da atividade com arcos direcionados para os lugares de entrada. De uma forma geral, a transição de término de uma atividade será a mesma transição de início da próxima atividade que foi listada. Quando se tem a rede sendo executada, uma ficha em um lugar indica que a atividade está sendo executada e várias fichas indicarão sua execução na multiplicidade do número de fichas. O disparo de uma transição de inicialização representa o início do processo e o disparo de uma transição de finalização indica a complementação da atividade e pode também representar o início da próxima atividade;
4. Para cada atividade ordenada: se um determinado lugar não foi criado, este deve ser criado e rotulado para cada recurso que deve estar disponível para iniciar a atividade. Todos os lugares de disponibilidade de recursos apropriados devem ser conectados com arcos a cada transição de entrada para a inicialização da atividade. Arcos de saída devem ser criados para conectar as transições de finalização seguintes à atividade para algum lugar de recurso representando recursos que se tornem disponíveis na complementação da próxima atividade; 5. Especificar a marcação inicial para o sistema.
Desenvolvimento do algoritmo e modelagem DO LABIRINTO em Redes de Petri
Neste artigo são explorados os robôs móveis. Pode-se definir um robô móvel como sendo um veículo munido de um sistema de sensoriamento e um sistema atuador, controlado por uma estrutura capaz de executar tarefas determinadas pelo seu projetista. Todo robô móvel autônomo desenvolve um conjunto de atividades em que se faz necessário o uso de dispositivos de entradas, que são os sensores, e um conjunto de dispositivos de saída. Para fazer o controle de todo o sistema geralmente são utilizados microcontroladores ou microcomputadores.
A estrutura básica de um robô é composta por três sistemas, que são o sistema de controle, sistema de acionamento e sistema sensorial.
O sistema de controle, principal sistema da estrutura, é responsável pelo funcionamento e comportamento do robô. Ele vai gerenciar todo o sistema visando por fim uma determinada tomada de decisão. Grande parte do que se pesquisa em robôs móveis utiliza Redes Neurais Artificiais (RNA). Porém, neste artigo, serão utilizadas as Redes de Petri.
Já o sistema sensorial, também conhecido por sistema de percepção, tem a tarefa de obter informações do atual estado do robô, como também do ambiente em que este está inserido. Existem diversos tipos de sensores que são utilizados, por exemplo, os de infravermelho e os do tipo chave.
E por fim tem-se o sistema de acionamento, que são os atuadores responsáveis, de fato, pelos movimentos do robô. Os motores elétricos são muito utilizados.
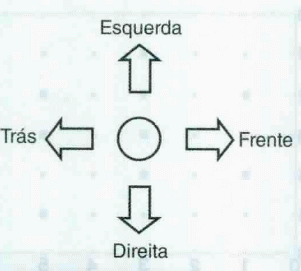
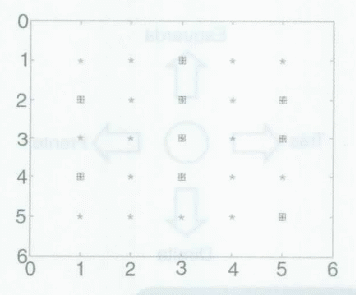
Neste trabalho é desenvolvido um algoritmo de mapeamento de labirintos através de um robô que se encaixa perfeitamente na terceira geração. Este estará munido de sensores capazes de detectar obstáculos que irão ser desviados e, ainda, terão os caminhos obstruídos gravados para que não o faça novamente. Os sensores deverão captar sinais de quatro posições perpendiculares entre si, como mostra a figura 2.
O robô se movimenta pelo labirinto, podendo assim descobrir o caminho correto a fazer para encontrar a saída. A tomada de decisão do robô é obtida através de testes realizados via sensores. Se o teste realizado for verdadeiro será realizado um passo, o que caracteriza um evento discreto. Com isso fica caracterizado um sistema a eventos discretos, que por sua vez pode ser modelado via Redes de Petri. No caso do presente trabalho, onde o objetivo é apenas a modelagem do sistema, os obstáculos encontrados pelos sensores serão identificados pelo número 1 na matriz principal. O caminho livre para o robô será dado pelo número O. Como o algoritmo implementado tem uma ordem de execução, e para isso deve-se ter um critério de tomada de decisão, ao fim do caminho percorrido pelo robô existirão lugares onde este não passará. Isso se deve ao simples fato de o robô ter tomado um caminho que o leve para a saída, sem que seja necessário andar por um devido lugar que o levaria a um caminho fechado.
Na figura 3 é mostrado um labirinto utilizado para realizar os primeiros testes do algoritmo. Pode-se notar que foi feito em uma matriz 5x5, tendo assim 25 lugares. Nesta, cada lugar é representado por um Aij correspondente, pelo qual o índice i representa o número da linha e o índice j representa o número da coluna.
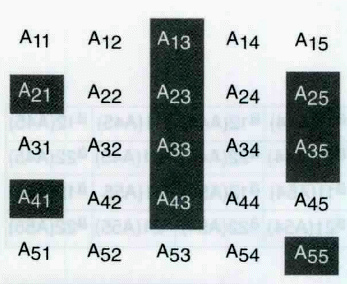
Para ilustrar o que foi dito a respeito de alguns lugares que não serão percorridos pelo robô, pode-se observar esse fato na figura 3. Os caminhos A31 e A51 não serão percorridos pelo robô, pois as direções adotadas na lógica implementada foram as apresentadas na figura 2. Assim, do ponto de vista da tomada de decisão na lógica, a direção DIREITA é tomada antes que o robô se movimente na direção TRÁS.
Por outro lado, o robô percorrerá o lugar A45, já que a direção FRENTE é tomada antes da direção DIREITA e ESQUERDA, contudo não será obtido sucesso, visto que a decisão tomada levará a um caminho fechado. Posteriormente ao teste para FRENTE será feito o teste para DIREITA, porém esse já foi um caminho percorrido pelo robô. Assim, o seguinte teste será para ESQUERDA, onde ele encontrará caminho livre, podendo assim continuar seu percurso até a saída desejada.
Para simplificar e ficar bem claro qual foi o critério utilizado para os testes de cada direção, tem-se que:
1° teste > Direção FRENTE
2° teste > Direção DIREITA
3° teste > Direção ESQUERDA
4° teste > Direção TRÁS
Cada célula da matriz principal será dividida em uma sub-matriz 2x2, na qual cada célula dessa sub-matriz indicará uma direção a ser tomada pelo robô. A célula a11 representará um passo para frente (F), a célula a12 um passo para direita (D), a célula a21 um passo para esquerda (E) e por fim se nenhum dos testes for positivo, ou seja, encontre caminhos livres, será realizado o teste na célula a22, e o robô dará um passo para trás (T). A figura 4 ilustra o vetor--linha que compõe cada célula da matriz principal.

Para ficar mais simples de visualizar o comportamento, são mostrados os valores que preenchem originalmente cada sub-matriz da figura 5.
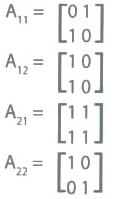

Na célula A11, onde se encontra primeiramente o robô, será feito o teste para saber se existe ao menos um O. Verifica-se que esse teste é verdadeiro e assim o programa entrará no primeiro teste condicional. Após isso, pela ordem direcional implementada, o teste será feito na célula a11 (A11) que representa andar para FRENTE. Realizado esse teste se verifica que o caminho para frente está livre, pois foi encontrado um O na célula. Com isso será atribuído o valor 2 à célula a11(A11) e só assim o robô dará o seu passo à frente. Quando esse passo for dado, o valor 2 será também atribuído a célula a22(A12) que representa andar para TRÁS.
Estando o robô na célula A12 , novamente será feito o teste para verificar a existência de no mínimo um 0. Confirmada a presença mínima do 0, inicia-se o teste direcional. Primeiramente testa a direção FRENTE sendo verificada presença de um 1, o que significa um caminho bloqueado. Após isso, verifica-se a direção DIREITA, e encontra-se um 0, ou seja, um caminho livre. Assim será atribuído o valor 2 à célula a12(A12), e o robô dará um passo a DIREITA. Dado esse passo, a célula a21 (A22) que representa a direção ESQUERDA receberá o valor 2. E o programa seguirá até a última célula seguindo a esse critério.
Esse valor 2 atribuído é utilizado para indicar que essa transição já foi utilizada pelo robô, mas que é um caminho em aberto ainda. No decorrer da explicação da lógica implementada ficará mais claro o uso dessa atribuição.
Quando o robô encontra um caminho sem saída, ele tenderá a voltar a um lugar onde será realizado um novo teste para encontrar um caminho livre que possivelmente será o correto. Quando esse fato ocorrer, e o teste para saber se existe algum 0 na sub-matriz for feito, este será negativo, pois esta deverá está preenchida por 1 e 2. Logo, o segundo teste condicional será realizado.
Esse segundo teste condicional funciona de forma semelhante ao primeiro, com uma pequena diferença. No primeiro teste os valores 0 eram substituídos por 2, ao passo que no segundo os valores 2 são substituídos por 1, indicando que aquele é um caminho incorreto e que o robô não deve voltar naquele lugar. Ficará mais simples o entendimento com a análise da figura 6.

Essa figura representa as células A44, A45, A54 e A55 da figura 3. Quando for realizado o teste na célula a11(A44) pela primeira vez será encontrado um 0, o que fará o robô dar um passo para a direção FRENTE. Com isso será atribuído o valor 2 nessa célula, o robô dará o passo a frente e será atribuído à célula a22(A45), que representa a direção TRAS. Quando o robô estiver na célula A45 será realizado o primeiro teste condicional e então será verificado que não existe nenhum O nessa sub-matriz, levando o programa ao segundo teste condicional. Feito isso, serão analisadas as direções FRENTE, DIREITA e ESQUERDA, nessa ordem, e se constatará que todos esses valores são 1, o que indica caminho fechado. A última alternativa do programa é verificar a direção TRÁS em que será encontrado o valor 2. Assim será atribuído o valor 1 na célula a22(A45), que representa a transição para trás, o robô dará um passo para trás e então será atribuído o valor 1 na célula a11(A44), que representa o passo à FRENTE. Isso significa que o robô não mais voltará para a célula A45, já que este é um caminho fechado.
Para facilitar, pode-se resumir o significado dos números como se segue abaixo.
• 1 > Caminho livre nunca percorrido pelo robô.
• 2 > Caminho fechado definitivamente.
• 3 > Caminho livre percorrido pelo robô. Para que fosse desenvolvido o código no MatLab foi elaborado um algoritmo, onde são descritos todos os passos do código. Esse algoritmo foi feito como está descrito a seguir.
• 1° passo: ler o sensor que indica a posição FRENTE.
• 2° passo: se encontrado um caminho livre, um passo a frente é dado e retorna-se ao 1P passo, se não, ler o sensor que indica a posição DIREITA.
• 3° passo: se encontrado um caminho livre, uma passo a direita é dado e retorna-se ao 19 passo, se não, ler o sensor que indica a posição ESQUERDA.
• 4° passo: se encontrado um caminho livre, uma passo a esquerda é dado e retorna-se ao 19 passo, se não, ler o sensor que indica a posição TRÁS, e como é o único caminho livre, ele dará um passo para o lugar que estava antes.
Resultados: simulações e modelagem
O algoritmo gera ilustrações que representam o labirinto encontrado pelo robô. Nessas ilustrações podem ser vistos três símbolos distintos que significam:
• Símbolo azul: trajetória percorrida pelo robô.
• Símbolo vermelho: paredes do labirinto.
• Símbolo preto: caminho não percorrido pelo robô.
O primeiro teste a ser realizado foi para um labirinto bastante simples composto de 25 lugares, dispostos em uma matriz 5x5, que foi mostrada na figura 3. Com o algoritmo implementado e executado, o resultado obtido para essa simulação está mostrado na figura 7. Observando essa figura, pode-se notar que pelo critério de tomada de decisão do algoritmo não foram percorridos apenas dois lugares de coordenadas (3,1) e (5,1). Além da ilustração gráfica, o programa implementado gera uma tabela com a ordem de lugares percorridos em formas de coordenadas. Na tabela 1 estão listados os caminhos na ordem percorrida pelo robô.
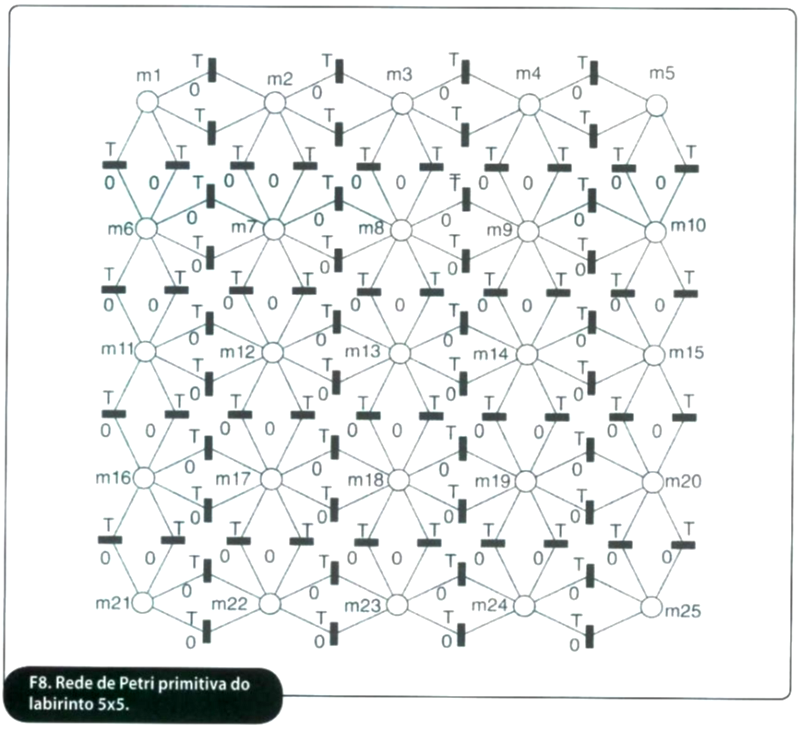
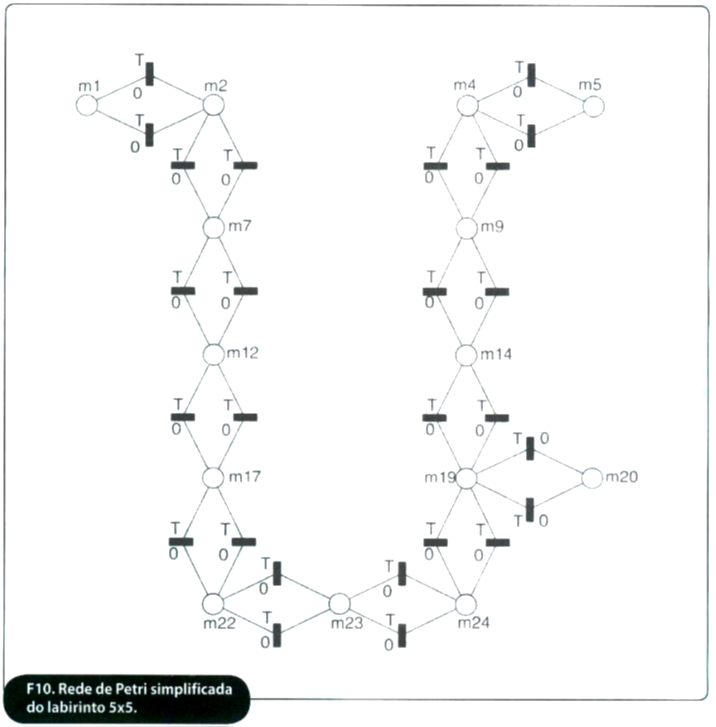
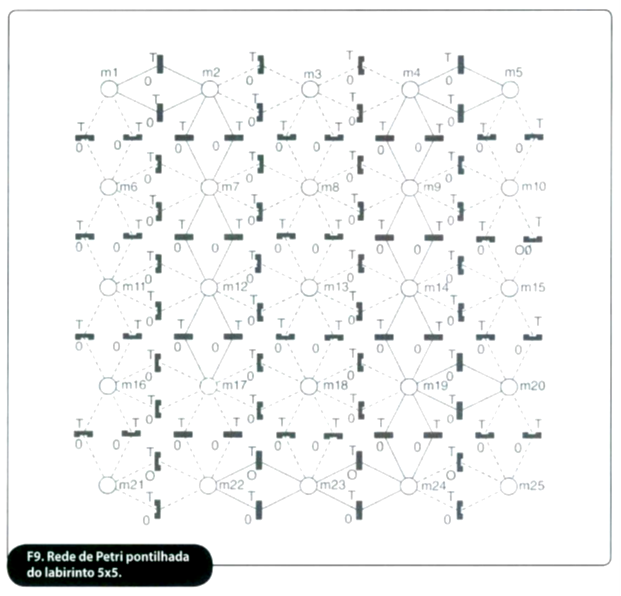
Com o algoritmo implementado foi feita a modelagem do sistema em Redes de Petri. Foi feito o modelo considerado primitivo, onde aparecem todos os lugares e transições do sistema completo. Após isso, os lugares e transições que são cancelados quando o programa for compilado são mostradas pontilhadas em outra figura. Por fim é mostrada a Rede de Petri em uma nova figura, contendo as transições de ida e volta, o que ilustra o algoritmo compilado.
As redes primitiva, pontilhada e simplificada são mostradas nas figuras 8, 9 e 10, respectivamente.
Conclusão
O trabalho desenvolvido teve como objetivos a criação de um algoritmo capaz de mapear labirintos e modelar esses labirintos após o código ser compilado. Tendo em vista que existem vários lugares que o homem tenta explorar nos dias de hoje, porém onde não é possível sua presença física, pode-se constatar a importância desse trabalho.
A escolha do MatLab para a realizar a implementação do algoritmo foi bastante apropriada, visto que este software permite uma manipulação de matrizes relativamente simples. Além disso, possui uma interface gráfica um tanto quanto ilustrativa, podendo assim gerar figuras gráficas que mostram os resultados obtidos, o que facilita o entendimento do usuário. Com o MatLab foi possível obter a sequência de lugares percorridos pelo robô, podendo assim elaborar uma tabela onde são mostrados os lugares na ordem encontrada pelo robô.
Para se obter a validação do modelo desenvolvido foram simulados, além do labirinto 5x5 mostrado, outros exemplos com maior número de lugares. Com isso pôde-se realizar testes para diversas situações, que foram impossibilitadas no labirinto de 5x5 lugares, devido à sua simplicidade. Com esses testes realizados verificou--se o bom comportamento do algoritmo para todas as situações testadas, tendo assim a comprovação do bom funcionamento do mesmo.