Dentro de muitos equipamentos eletrônicos bate um "coração invisível" que determina com um ritmo preciso o seu funcionamento. Nos relógios, cronômetros, computadores, equipamentos de comunicações e muitos outros aparelhos, minúsculos cristais de quartzo vibram com precisão garantindo que seus circuitos funcionem de maneira totalmente ordenada e sincronizada. É difícil prever o que seria da Eletrônica em nossos dias sem a presença desses elementos.
A importância dos cristais de quartzo e seu funcionamento configuram o tema central desse artigo, útil para todos os profissionais de Eletrônica ou daqueles, de uma forma ou de outra, utilizam equipamentos eletrônicos em seu trabalho.
O que faz com que um relógio eletrônico mantenha seu ritmo exato, independentemente das variações das condições ambientais, das diversas situações em que ele deve funcionar e até mesmo do próprio estado da sua bateria?
O que faz com que todas as operações de um computador sejam totalmente sincronizadas em uma velocidade enorme, com um mínimo de variações?
O que faz com que os transmissores das estações de rádio e TV e das estações de telecomunicações mantenham suas frequências com grande precisão, não interferindo umas nas outras, permitindo que o leitor as sintonize sempre no mesmo ponto do mostrador de seu rádio, ou sempre que tocar a mesma tecla de seu televisor, ou ainda quando utilizar seu telefone celular?
Se o leitor respondeu que é o cristal de quartzo, acertou, mas acreditamos que na maioria dos casos, essa resposta deve estar acompanhada de uma grande interrogação: mas como um cristal de quartzo pode fazer isso?
A maioria dos equipamentos eletrônicos que exija alguma espécie de sincronismo preciso, ou seja, um "relógio interno" para funcionar, aproveita as propriedades dos cristais de quartzo.
Esses cristais são instalados em invólucros que possibilitam seu acoplamento a um circuito e, normalmente, podem ser encontrados com as aparências mostradas na figura 1.
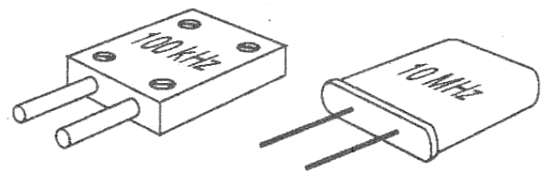
Evidentemente, os tamanhos e as formas podem variar bastante em função da aplicação, da frequência e do tamanho do próprio cristal.
O funcionamento da pequena peça de cristal transparente que é colocada nesses invólucros é algo que pode maravilhar tanto pela sua simplicidade como pelo seu significado. Mais uma vez, a Natureza manifesta (em coisas simples) propriedades que podem ser sofisticadas a ponto de significar todo o sincronismo das operações que seu computador realiza ou a eficiência com que seu telefone celular pode ser comunicar com uma estação radiobase.
O Cristal de Quartzo
Os cristais são estruturas em que os átomos se dispõem de uma forma ordenada que se repete em toda a sua extensão. Assim, forma-se uma espécie de rede de átomos com uma disposição totalmente ordenada em toda sua extensão, conforme ilustra a figura 2.
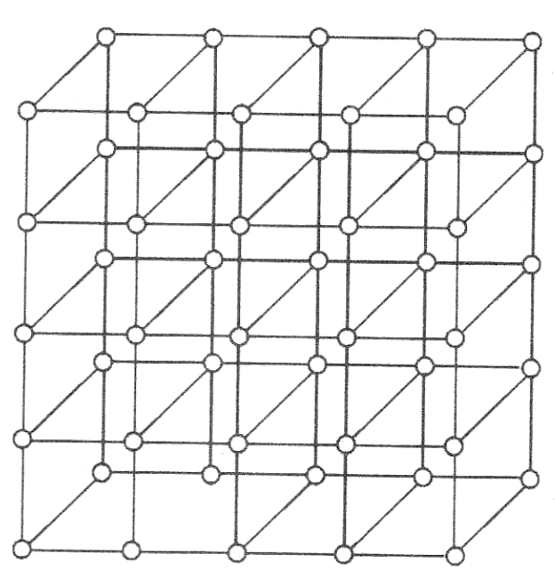
Os átomos de um cristal não precisam ser, necessariamente, todos do mesmo elemento. Um cristal pode ser formado por átomos de dois tipos como, por exemplo, de um metal como o silício, o alumínio, etc., e o oxigênio como elemento "intruso".
Muitos cristais de grande efeito decorativo e também muito valiosos, como o rubi, a turmalina etc., são estruturas formadas por átomos de dois tipos, normalmente um deles sendo o oxigênio. A maioria dos cristais apresenta uma estrutura perfeitamente simétrica, o que significa que as forças de natureza elétrica manifestadas pelos átomos no seu interior são balanceadas, e nada de anormal acontece ou é notado em termos de seu comportamento.
No entanto, dependendo da disposição dos átomos que formam o cristal, pode ocorrer que haja uma assimetria em relação às forças elétricas manifestadas entre partículas. O resultado disso é a manifestação de forças de natureza elétrica em determinadas condições.
Assim, existem os casos em que essa assimetria se manifesta de tal maneira que as faces do cristal predominem cargas de determinadas polaridades, ou seja, o material permanece constantemente carregado com cargas estáticas, de acordo com a figura 3.
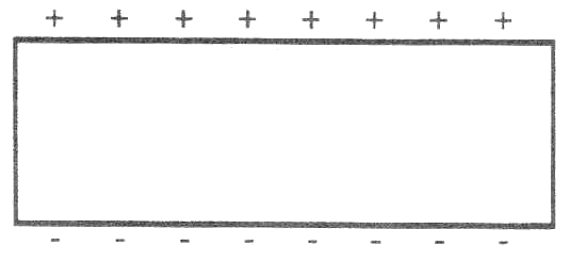
Um material desse tipo é denominado piroelétrico, ou seja, trata-se de um eletreto. As cargas que esse material manifesta são intrínsecas, bem diferente das cargas que um corpo acumula quando, por exemplo, o atritamos com outro.
Mas, o caso que nos interessa é um pouco diferente: existem cristais que em condições normais não manifestam qualquer desequilíbrio elétrico no seu interior. Entretanto, quando esses cristais sofrem algum tipo de deformação homogênea, tal como uma compressão, extensão ou torção, aparecem cargas elétricas localizadas, ou seja, eles se tornam polarizados.
Qualquer cristal que não possua um centro de simetria, apresenta essa propriedade, que é a de ser piezoeléctrico.
A intensidade com que o efeito se manifesta depende da direção do deslocamento que os átomos sofrem com a deformação em relação às suas posições originais de equilíbrio.
O efeito contrário também pode ser observado: se aplicarmos às faces de um cristal esse tipo de tensão elétrica, ele se deformará.
Um material que pode manifestar essa propriedade é o quartzo, isso quando seus cristais são cortados de determinada maneira, o que é indicado na figura 4.
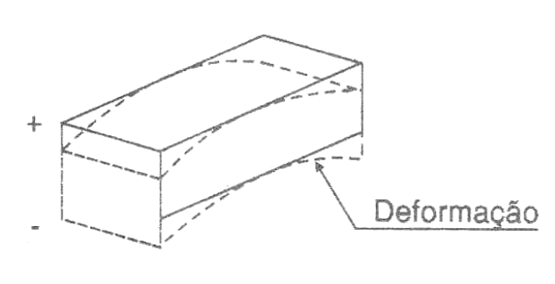
Desse modo, o corte de um cristal de quartzo comum, que é uma forma de óxido de silício (SiO2), em qualquer das maneiras mostradas na figura, resulta em cristais piezoeléctricos.
Ressonância
Os cristais piezoeléctricos de quartzo, em consequência do fato de apresentarem uma polarização elétrica em suas faces devidos às deformações, têm outras propriedades importantes que relatamos a seguir. Uma dessas propriedades é a ressonância.
Qualquer corpo possui uma frequência natural de vibração. Quando batemos numa lâmina de metal presa numa morsa, vide figura 5, esta lâmina tende a vibrar numa única frequência que depende de seu formato, tamanho e material de que é feita.
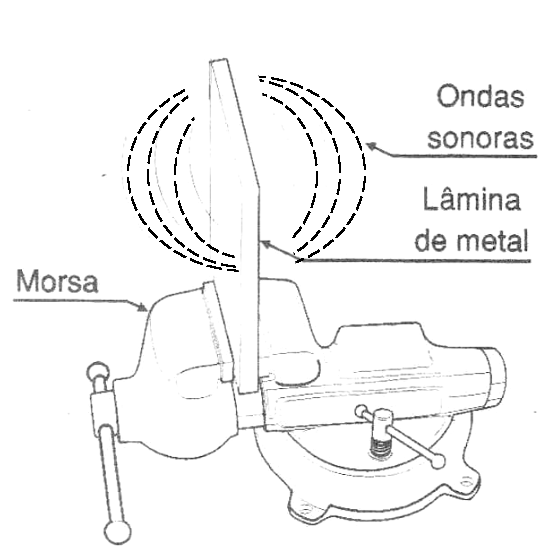
As vibrações mecânicas fazem com que forças elásticas entrem em ação determinando o modo como essas vibrações se realimentam e, portanto, a frequência natural com que o corpo tende a oscilar.
Componentes
Esse é o princípio de funcionamento do diapasão que produz sempre a mesma nota musical quando excitado mecanicamente, ou das teclas de um xilofone, conforme mostra a figura 6.
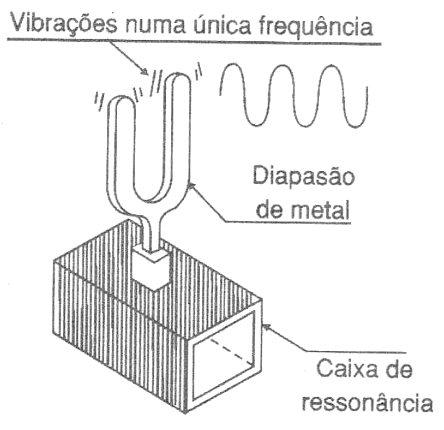
Até o ar no interior de um tubo de órgão ou de um instrumento musical, vibra em frequência que depende de suas dimensões, o que resulta no princípio de funcionamento de todos os instrumentos musicais de sopro.
No caso do cristal de quartzo, as suas dimensões e também as forças elásticas que agem no seu interior, e que dependem da direção de sua atuação determinada pelo corte, fazem com que ele tenda a vibrar sempre em uma única frequência quando excitado mecanicamente ou eletricamente.
Em outras palavras, podemos dizer que um cristal de quartzo se comporta, quando excitado, como um diapasão elétrico. Para termos então correntes elétricas ou sinais de determinadas frequências a partir de um cristal de quartzo, basta cortar esse cristal com as dimensões apropriadas e excitá-lo eletricamente de modo que ele entre em vibração.
As vibrações então ocorrerão na sua frequência de ressonância, ou ainda num múltiplo dessa frequência, ou seja, em frequências harmônicas.
O que sucede em relação às frequências harmônicas pode ser entendido tomando por sua base uma corda de violão, observe a figura 7.
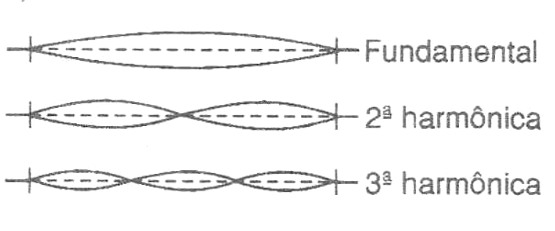
Uma corda de violão quando excitada, pode vibrar somente de determinadas maneiras, as quais são determinadas por seus pontos fixos, ou seja, pelos nodos, conforme mostra a figura.
Assim, a frequência mais baixa que ela pode produzir é a denominada fundamental, que é aquela em que temos os dois nodos nos pontos de fixação da corda e um ventre em seu meio.
Mas, a vibração poderá ocorrer também de tal forma que tenhamos um segundo nodo no meio, o que corresponde ao dobro da frequência, ou à segunda harmônica.
Da mesma forma, podemos ter três, quatro, cinco, etc., nodos que permitirão que a corda vibre sempre em frequências múltiplas da fundamental.
O mesmo acontece com um cristal, pois ele pode ser forçado a operar em modos de vibração que venham a produzir frequências harmônicas da denominada fundamental.
Esta possibilidade é interessante se considerarmos que, quanto maior for a frequência que um cristal deve produzir, menor devem ser suas dimensões, o que nos leva a um ponto em que o componente se torna muito pequeno e o cristal tão fino que fica extremamente delicado.
Podemos, então, usar os cristais dessa forma para produzir sinais que tenham frequências muito mais elevadas que a fundamental e que, de outra forma, exigiriam componentes extremamente finos e delicados.
Os Cortes
Ao explicarmos no início que o modo como um cristal é cortado influi na maneira como ele pode vibrar e na intensidade com que o efeito piezoeléctrico se manifesta, devemos ter apenas três orientações possíveis.
Na prática, a Eletrônica pode aproveitar muito mais orientações e assim existem muitos tipos de cortes, os quais resultam em cristais com aplicações específicas.
Na figura 8 temos uma ilustração onde são mostrados todos os tipos de corte com as suas respectivas denominações.
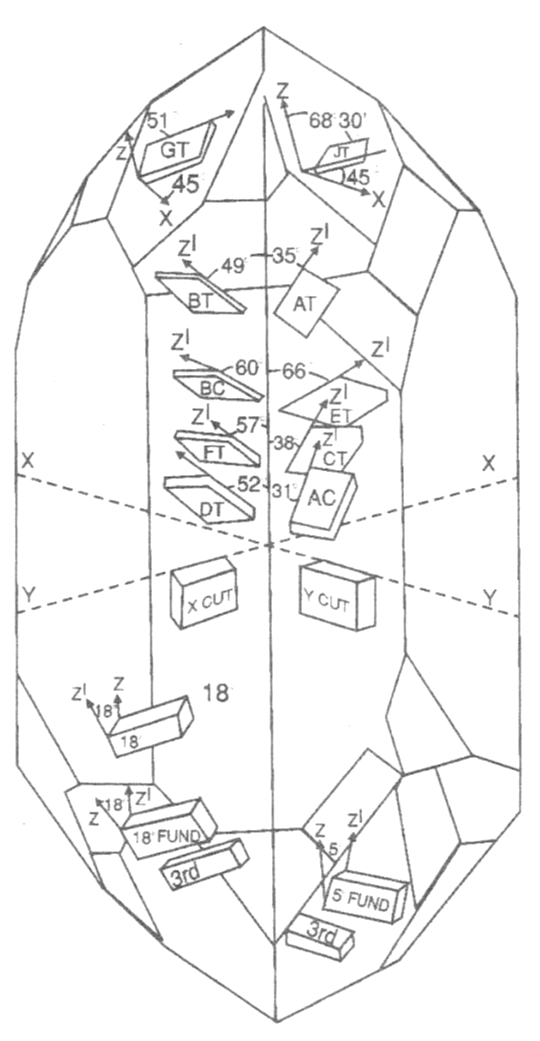
Esses cortes irão determinar não só o modo segundo o qual o cristal vibra quando excitado, na sua aplicação principal, como também a faixa de frequências e o uso a que se destina. Temos, então, os seguintes cortes principais:
• Duplex 5 X — Designação J: Nesse corte, o cristal vibra no sentido de seu comprimento e pode operar em frequências entre 0,8 e 10 kHz. Trata-se, pois, de um corte para baixas frequências, obtendo-se um coeficiente nulo de temperatura na temperatura ambiente.
• XY: Nesse corte, o cristal pode vibrar tanto no sentido do comprimento quanto na largura, numa faixa de frequência entre 3 e 50 kHz. Também temos neste caso um corte destinado a operação em baixas frequências.
• NT — designação N: Os cristais com este corte vibram no sentido de seu comprimento em frequências entre 4 e 150 kHz, sendo indicados para aplicações em osciladores de baixa frequência e filtros. Uma estabilidade de frequências de 0,0025% pode ser obtida na temperatura ambiente sem a necessidade de controles de temperatura.
• +5 X — designação H: O cristal neste corte vibra no sentido de flexionar-se numa faixa de frequências de 5 a 140 kHz. As variações relativamente grandes da frequência deste cristal com a temperatura, limitam suas aplicações a filtros em ambientes com temperaturas controladas. Dentre as dificuldades que podem ser citadas para este cristal está a relacionada com sua fabricação, visto que ele deve ser uma barra fina e longa fixada em suporte especial.
• BT — designação B: Nesta modalidade de corte o cristal vibra no sentido de sua espessura e em uma faixa de frequências compreendida entre 1 e 75 kHz. Dentre as dificuldades apresentadas por este tipo de cristal está também a relacionada à sua fabricação.
• -18-1/2 X — designação F: Neste corte, o cristal vibra no sentido de seu comprimento em uma faixa de frequências que pode ficar entre 50 e 250 kHz. Este tipo de cristal é utilizado em filtros e pode ser encontrado em aplicações multi eletrodos.
• +5 X — designação E: Os cristais que apresentam este corte vibram no sentido de seu comprimento numa faixa de frequências de 50 a 250 kHz, sendo empregados em aplicações como filtros de baixa frequência graças a seu baixo coeficiente de temperatura, que lhe dá uma boa estabilidade.
• DT — designação D: Este tipo de cristal tem suas oscilações rentes às faces e pode operar em frequências na faixa de 80 a 500 kHz. Ele é usado como calibrador e base de tempo em frequencímetros, além de transmissores de FM e TV. No entanto, ele não pode operar satisfatoriamente acima de 500 kHz.
• MT — designação M: As vibrações neste tipo de cristal acontecem ao longo de sua extensão numa faixa de frequência de 50 a 250 kHz. Seu baixo coeficiente de temperatura torna-se ideal para controle de osciladores e filtros. Todavia, trata-se de um tipo de cristal pouco usado porque existem unidades mais compactas que o substituem.
• GT — designação G: Neste cristal as vibrações ocorrem no sentido de sua extensão em uma faixa de frequência de 85 e 400 kHz. É o tipo de corte que apresenta a maior estabilidade, não variando sua frequência em mais que uma parte por milhão em um faixa de 100 graus Celsius. É utilizado em padrões de frequência nos quais a estabilidade sem o controle de temperatura seja essencial. A desvantagem está no seu preço, uma vez que é o mais caro de todos os tipos devido ao grande trabalho que existe em se encontrar a direção exata de seu corte
• CT — designação C: As vibrações neste cristal manifestam-se rentes à superfície de suas faces numa faixa de frequências de 300 kHz a 1,1 MHz. Trata-se de um cristal com coeficiente de temperatura nulo nas baixas frequências. É utilizado em filtros e osciladores que não necessitam do controle de temperatura de funcionamento. Entretanto, como desvantagem, ele é difícil de ser fabricado em frequências muito baixas devido às suas dimensões.
• X: Neste corte, o cristal vibra ao longo de suas extensões podendo fazer isso em uma faixa de frequência que vai de 350 kHz a 20 MHz. Trata-se de um tipo de cristal mecanicamente estável e de baixo custo. No entanto, além de coeficiente de temperatura algo elevado, ele tem tendência a mudar seu modo de oscilação.
• SL: As vibrações deste cristal ocorrem rentes à face, mas acopladas à flexão, isso numa faixa de frequências entre 300 e 800 kHz. As características elétricas deste cristal são similares às do corte DT, porém, ele é maior, possui melhor Q e uniformidade de características acima de 300 kHz. Estas características o tornam ideal para uso em filtros.
• Y — designação Y: Este cristal vibra com ondas superficiais acopladas por flexão numa faixa de frequências que vai de 500 kHz a 20 Mhz. Este tipo de cristal é o mais ativo.
• AT — designação A: Este tipo de corte faz com que o cristal vibre no sentido de sua espessura em uma faixa de frequências de 550 kHz a 20 MHz para o modo fundamental, e de 10 MHz a 60MHz nos modos em terceiro sobre tom. As características excelentes de temperatura e frequência fazem deste tipo de corte o escolhido para os casos onde a frequência não deva se alterar com as variações de reatância do oscilador. Estas características tornam-se bastante usadas no controle de osciladores de altas frequências. Dentre as desvantagens apresentadas podemos citar a dificuldade de fabricação.
Os Osciladores
Um cristal sozinho não pode entrar em vibração espontaneamente. A excitação que coloca um cristal em oscilação e depois a mantém, é obtida por meio de um circuito especial. Esse circuito, conforme sugere a figura 9, nada mais é do que um amplificador que tem um elo de realimentação. Ao conjunto assim obtido denominamos "oscilador".
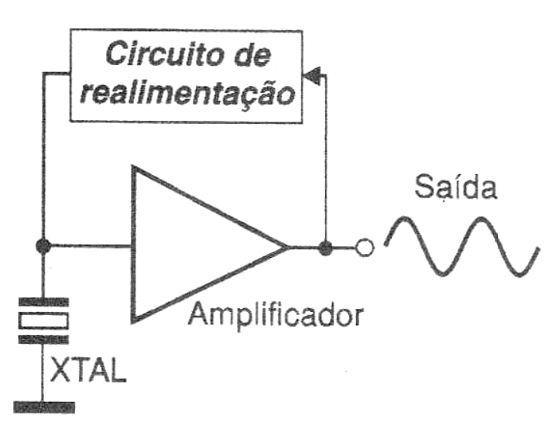
Dessa forma, os circuitos que produzem sinais com certas frequências e são controlados por cristais de quartzo, são denominados osciladores controlados por cristal, ou simplesmente osciladores a cristal (utiliza-se também a abreviação XTAL-OSC).
Para que tenhamos um oscilador a cristal é preciso que o circuito empregado na excitação tenha um certo ganho, ou seja, que o sinal obtido na sua saída seja maior do que aquele que se requer para excitar o cristal.
Componentes
Se isso não ocorrer, o sinal de saída que serve para excitar de novo o cristal, ficará cada vez mais fraco, e o que teremos é a produção de uma oscilação amortecida, conforme ilustra a figura 10.
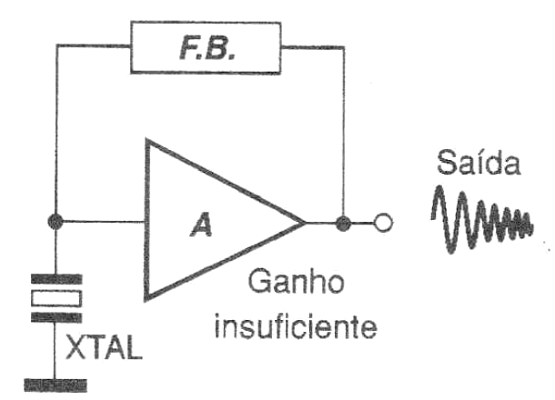
Com um ganho maior que 1,0, "sobra" sempre um pouco de sinal necessário à realimentação que mantém as oscilações e que pode ser usado no circuito externo.
Existem centenas de aplicações eletrônicas em que os cristais controlam a frequência de osciladores, cujos sinais, (que são correntes de determinadas frequências) são os responsáveis pelos seus ritmos de funcionamento.
Aplicações para cristais
Algumas aplicações dos cristais se destacam. Por isso, será interessante que os leitores as conheçam.
Relógios
O ritmo de um relógio mecânico é dado pelo balanço de um mecanismo controlado por uma mola. A tensão dessa mola determina o ritmo das oscilações.
Os relógios modernos são eletrônicos e seu ritmo é dado por um cristal. Mesmo que exista um micromotor acionando os ponteiros, veja a figura 11, seu ritmo e, portanto, a precisão do relógio depende do cristal.
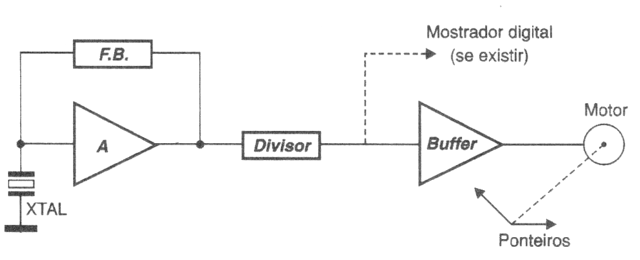
Evidentemente, o cristal de um relógio não tem a frequência mínima que estamos acostumados a visualizar, que é a de 1 Hz, ou um impulso por segundo. Seria muito difícil fabricar um cristal com essa frequência (e ele também seria muito grande). Assim, os relógios utilizam cristais de frequências mais altas, sendo elas divididas por circuitos apropriados de modo a se obter um ritmo que seja ideal para o andamento do relógio.
A precisão obtida num sistema deste tipo é excelente, com pequenas variações que normalmente ocorrem em vista das diferentes temperaturas que o relógio encontra nos ambientes em que trabalha.
O anúncio de que um relógio é de quartzo refere-se justamente à presença deste elemento no circuito, determinando assim seu ritmo preciso de funcionamento.
Devido ao espaço limitado que existe num relógio de pulso, evidentemente, os cristais usados devem ter dimensões muito pequenas, o que implica também que eles não consigam oscilar em frequências muito baixas. Assim, os minúsculos cristais dos relógios produzem oscilações de vários mega-hertz para a divisão posterior pelos circuitos de que já falamos.
Computadores e microcontroladores
Os computadores e microcontroladores e mesmo outros, possuem circuitos que operam segundo o que se denomina lógica sincronizada.
Todos os circuitos devem operar sincronizados por um determinado sinal de frequência única, denominado "clock", o qual determina quando cada um deve realizar uma determinada operação, atender uma interrupção ou estar pronto para emitir o resultado de uma operação.
Se isso não fosse feito, uma determinada etapa de um computador poderia estar já somando o valor de um dado a outro armazenado numa célula, antes mesmo que o outro tivesse chegado, dando com resultado um valor completamente errado.
Todos os circuitos de um computador são sincronizados por um oscilador único que determina seu ritmo de andamento.
Dessa forma, quando dizemos que um computador "roda" a 3 GHz e, portanto, é muito mais rápido que outro que só "roda" a 2 GHz, estamos nos referindo à frequência do clock, que é justamente determinada por um oscilador por cristal, observe a figura 12.
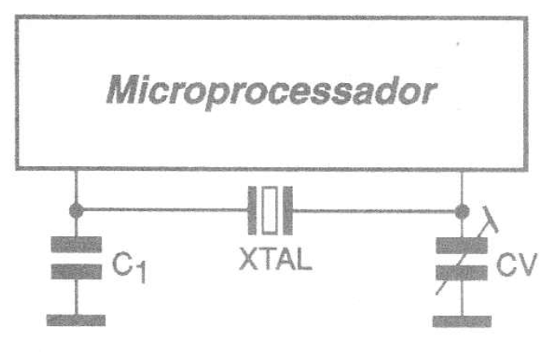
A velocidade de um computador não pode ser alterada simplesmente pela troca de sinal de seu clock. A escolha de um determinado valor de frequência para um cristal de um computador depende da capacidade de seus circuitos operarem com tal frequência.
Se um computador que utiliza componentes projetados para operar com frequência máxima de 20 MHz, receber um sinal de clock de 40 MHz , ele não irá conseguir operar satisfatoriamente.
Um problema que surge na operação em velocidade maior (denominada over-clock) é que há uma dissipação de calor maior. Esse fato justifica a existência de uma chave "turbo".
Em muitos computadores antigos que os dotam de duas velocidades: uma é a frequência original do clock dada pelo cristal, e a outra dada por um divisor por 2 que permite a operação na metade da velocidade.
Em condições limites, num ambiente quente ou quando o computador tiver que funcionar por horas seguidas, se não estivermos com um programa que necessite de alta velocidade, será interessante aliviar os circuitos de um aquecimento maior com a operação em menor velocidade.
Podemos dizer, de uma forma geral, que o oscilador de clock de um computador funciona como um "maestro" que determina seu ritmo e funcionamento de modo que tudo corra em harmonia. A quebra da harmonia poderá significar erros graves e a própria inoperância do aparelho.
É importante observar que nos computadores mais modernos existe um oscilador de frequência única que determina a frequência básica de operação de um circuito de entrada. Através de programações por meio de jumpers ou ligações, é possível modificar os circuitos que ele controla de modo a se programar a velocidade do processador. Dessa forma, o profissional da Informática pode perfeitamente alterar a velocidade de um processador sem mexer no oscilador, apenas mudando a programação.
É claro que o risco de se fazer esta operação de "overclock" é o que já explicamos: rodando mais rápido que o recomendado, pode-se levar o circuito a falhas ou mesmo sobreaquecimento.
Existem instrumentos de medida onde a precisão da medida depende fundamentalmente da precisão com que se pode estabelecer um intervalo de tempo de referência.
Esse é o caso de frequencímetros em que a medida de uma frequência é feita contando-se o número de ciclos num intervalo de tempo conhecido, conforme mostra a figura 13.
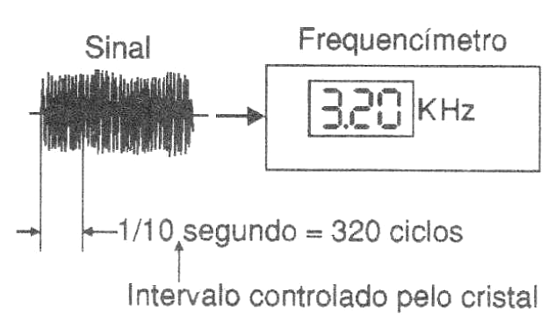
Por exemplo, num frequencímetro comum podemos fixar em 1/10 de segundo o intervalo de contagem dos pulsos ou "amostragem". Assim, se nesse intervalo, para um sinal de frequência a ser medida, forem contados 5000 ciclos, então a frequência desse sinal (projetada no mostrador) será de 50 kHz.
Os próprios circuitos internos fazem a multiplicação de valor ou a colocação do ponto decimal, desprezando os dígitos menos significativos, quando necessário.
Outras aplicações
Telefones sem fio, telefones celulares, instrumentos de medida de diversos tipos, walk-talkies, televisores em cores, videocassetes e DVDs são alguns outros exemplos de aparelhos em que encontramos os cristais exercendo funções decisivas relacionadas com o controle de frequência.
Nos telefones sem fio, os cristais determinam a frequência de operação das estações garantindo, assim, uma estabilidade que de outra forma não poderia ser obtida. Se o ajuste da frequência fosse feito por circuitos sintonizados comuns (LC), a possibilidade de "escape" do sinal seria muito maior, resultando na necessidade constante de reajuste do aparelho com a consequente perda da confiabilidade.
Nos walk-talkies, os cristais determinam com precisão o canal em que os aparelhos devem operar, fixando a frequência tanto do receptor quanto do transmissor.
Finalmente, nos televisores, encontramos cristais nas etapas de processamento de cores, fixando a frequência dos circuitos de modo a detectar esse sinal com precisão.
Conclusão
O leitor teve, neste artigo, apenas uma amostra da importância dos cristais de quartzo na Eletrônica. Um aprofundamento maior poderá ser importante se o leitor for trabalhar com esses componentes. A variedade de tipos de frequências leva à necessidade de conhecer todas as propriedades específicas de cada um para que a escolha de um novo projeto seja aquela que o leve ao melhor desempenho.


















