Dando continuidade ao estudo do Osciloscópio, abordamos nesta segunda parte do Curso sobre o Osciloscópio – Parte 1 (INS646)
Osciloscópio Digital
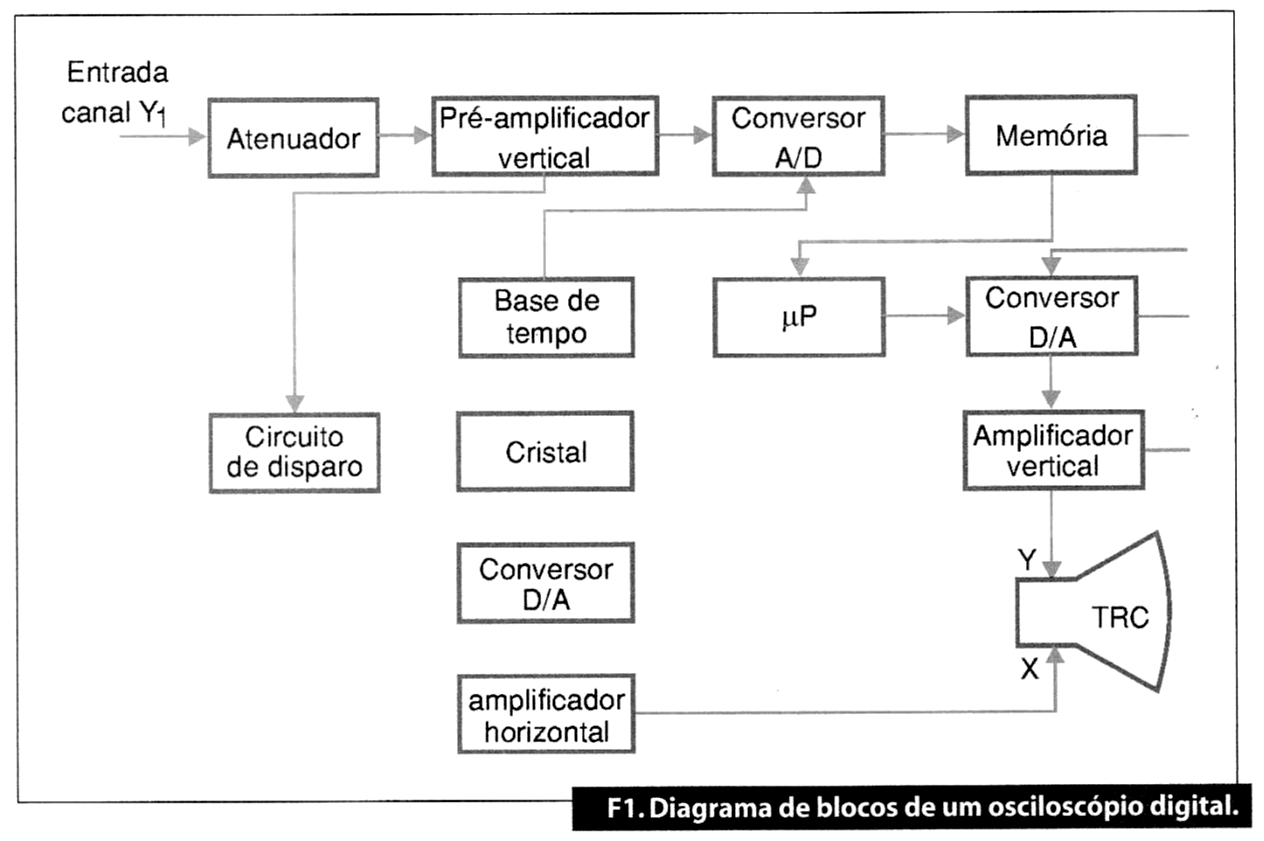
Um osciloscópio digital tem etapas parecidas com as de um osciloscópio analógico, embora funcione de forma totalmente diferente (como mostra a figura 1).
Em primeiro lugar, e à semelhança do osciloscópio analógico, tem-se uma etapa atenuadora e um pré-amplificador vertical que amplifica o nível de sinal ao valor adequado para as etapas seguintes.
Do pré-amplificador vertical, o sinal deriva em direção a dois circuitos: por um lado, aplica-se ao comparador que faz parte do circuito de disparo, mediante o qual selecionaremos o instante do sinal que dará lugar à varredura horizontal do spot na tela. Por outro, aplica-se a um conversor analógico / digital (A/D), no qual cada amplitude instantânea do sinal que se visualiza é convertida num código binário.
Para esta conversão é necessária uma amostra do sinal; isso quer dizer que se mede a amplitude do sinal em tempos iguais. Para levar a cabo esta amostra, sem erros de medida, é necessário que os pulsos de amostra tenham uma frequência extremamente estável. Consegue-se isso com um oscilador a cristal, que é disparado quando recebe o pulso do início de exploração do circuito de disparo.
Observe-se no diagrama de blocos que o oscilador a cristal aplica também os seus pulsos retangulares a um conversor digital/analógico (D/A). Este conversor é necessário, já que para a varredura horizontal do spot necessitamos de uma tensão em dente de serra, e o oscilador a cristal gera apenas pulsos retangulares. Com o conversor D/A obtemos uma tensão em dente de serra muito estável e linear, válida para aplicar às placas de deflexão horizontal do tubo de raios catódicos previamente amplificadas ao valor adequado pelo amplificador horizontal.
Prossigamos o percurso do sinal em direção às placas de deflexão vertical do tubo. Frisamos que o sinal analógico foi convertido em pulsos binários à saída do conversor A/D. Assim pois, a partir deste ponto, o sinal pode ser tratado como qualquer sinal digital e guardá-lo num circuito de memória. Do circuito de memória o sinal pode tomar dois caminhos: um para o conversor D/A onde se converte de novo numa onda analógica de forma igual à original.
O outro caminho para o sinal digital é em direção a um microprocessador (.tP). O [IP permite efetuar medidas automáticas dos parâmetros do sinal, tais como intervalos de tempo, tempos de subida e de descida, amplitude, frequência e visualizar estes dados na própria tela mediante caracteres alfanuméricos (osciloscópios Read - Out) ou enviá-los para uma impressora.
Amostragem do sinal nos osciloscópios digitais
O conversor analógico - digital é a etapa chave do funcionamento dos osciloscópios digitais e tem por função transformar o sinal analógico numa série de pulsos elétricos.
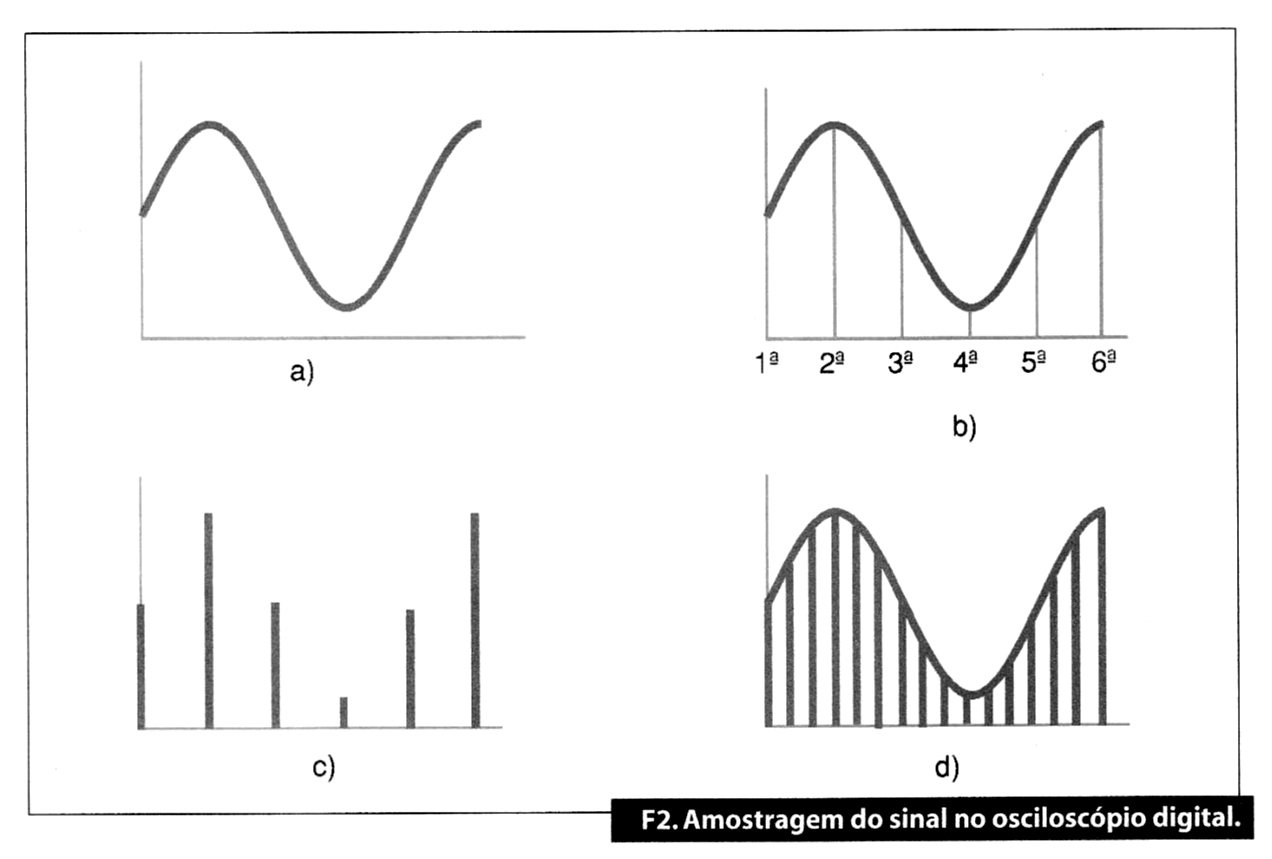
Para que a amostra do sinal seja correta e se apresente na tela um sinal que corresponde ao real, a amostra deve realizar-se, pelo menos, a uma frequência dupla da maior harmônica do sinal (figura 2).
a) Onda senoidal que se pretende amostrar (figura 2a);
b) Pontos de amostragem. Na amostra da onda (figura 2b) observa-se que, desde que se inicia o ciclo até que volte a passar pelo mesmo ponto, efetuaram-se quatro amostras, e com elas obteremos um total de quatro valores ou amplitudes para codificar;
c) Pulsos obtidos como consequência dessa amostragem. Estes pulsos de diferentes amplitudes, serão os que se codificam de imediato em binário (figura 2c).
Se levarmos a cabo uma amostragem a uma frequência maior, por exemplo triplicando a frequência do oscilador de cristal, obteremos uma série de valores cujo conjunto se aproxima mais da forma de onda original.
Disto se deduz que, quanto maior for a frequência da amostragem, melhor será a informação que obtemos e mais próximo estaremos da forma de onda do sinal, pelo que poderemos reproduzi-la com a máxima fidelidade (figura 2d).
Como a frequência da amostragem está limitada tecnologicamente, para aumentar o número de amostras por período deve reduzir-se o limite da largura de banda do aparelho, com o fim de, pelo menos, poderem efetuar-se duas amostras por período.
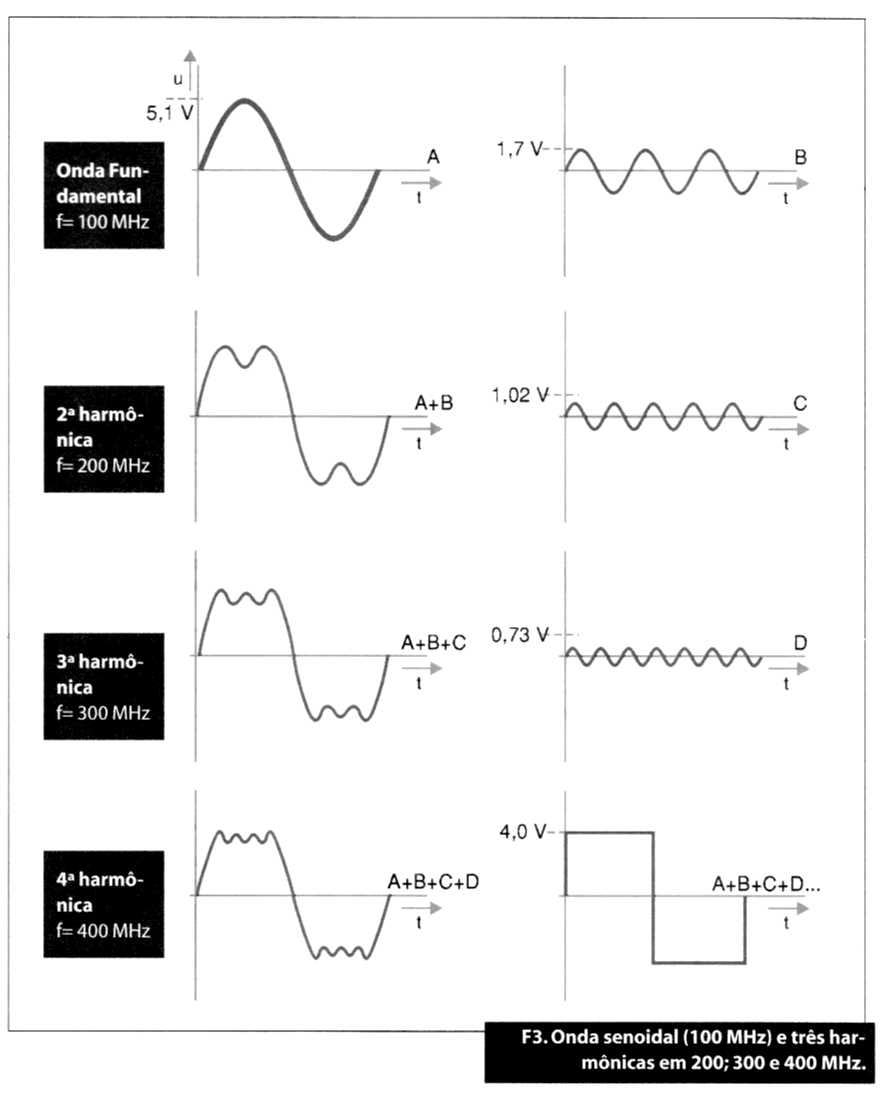
O problema complica-se perante a presença de harmônicas do sinal de entrada. Um caso típico é o de uma onda retangular ou quadrada.
Toda a onda retangular é formada por uma onda senoidal de igual frequência e um número praticamente infinito de harmônicas desta onda fundamental, tal como se mostra graficamente na figura 3.
A velocidade de representação nos osciloscópios digitais é lenta, já que é a soma de vários tempos: de quantificação, de voltar à memória, de processamento do sinal e de conversão do digital a analógico.
Medida de Frequências
Para medir a frequência de um sinal com o osciloscópio pode-se proceder das seguintes maneiras:
• Com a base de tempo calibrada;
• Por meio das figuras de Lissajous.
Com a base de tempo calibrada
Este método é o mais simples. Consiste simplesmente em aplicar o sinal a uma entrada vertical e ajustar a varredura até se obter na tela um ou mais ciclos do sinal
Obs.: O número de ciclos que aparece na tela é o que corresponde ao número de vezes que a frequência do sinal é superior à frequência de varredura. Se ambas as frequências são iguais, obtém-se um só ciclo. Se não se consegue obter um só ciclo na tela é porque a frequência de varredura não alcança o alto valor da frequência do sinal.
Contando o número de divisões de um ciclo do sinal e multiplicando-o pela velocidade de varredura da base de tempo (s/div., ms/ div., s/ div.) obtemos o Período (T), fazendo o seu inverso obtemos a frequência do sinal (f =1/T).
Por meio das figuras de Lissajous
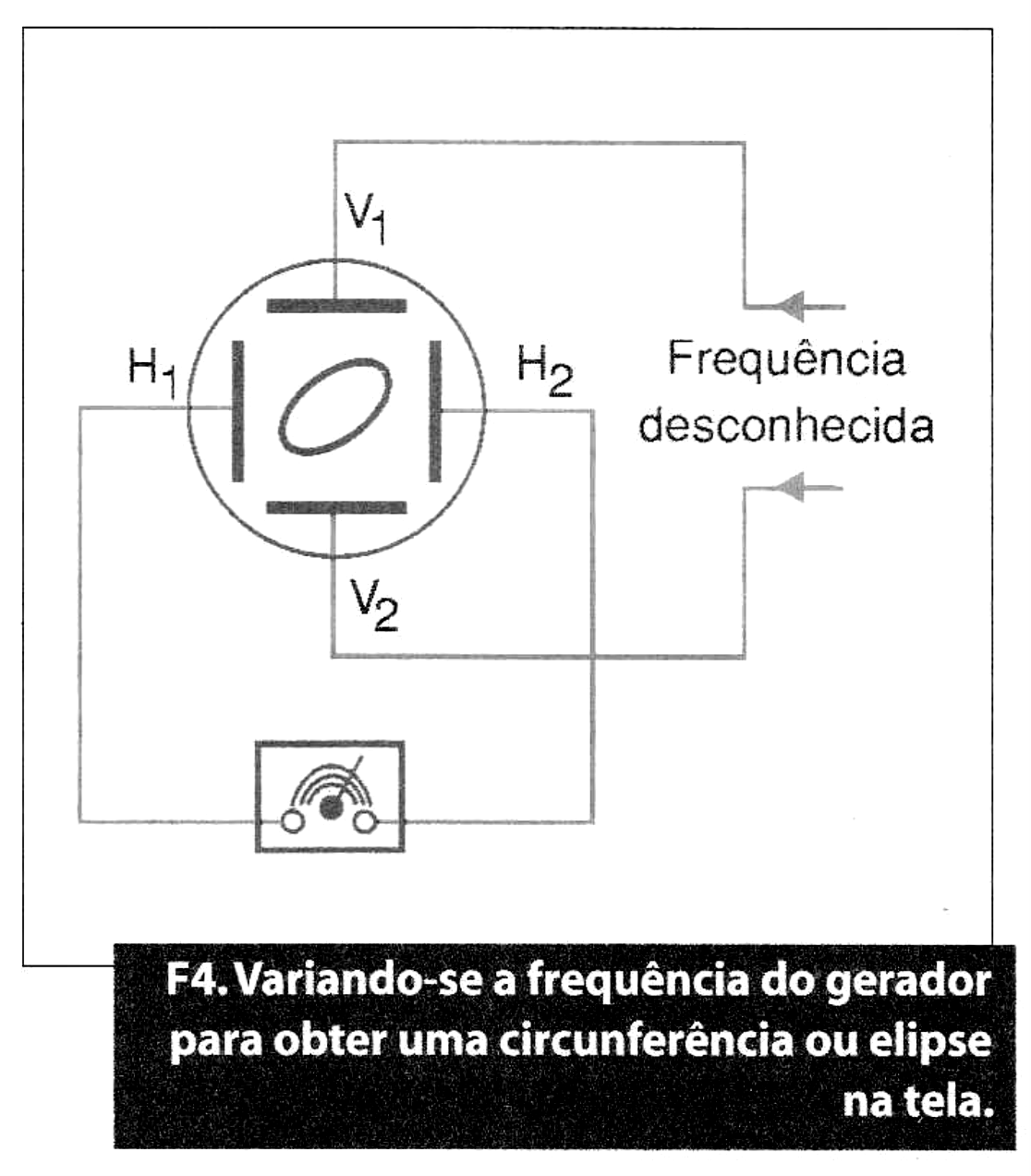
Pressionar o botão XY (que desliga a base de tempo) e aplicar o sinal de frequência desconhecida às placas de deflexão vertical do osciloscópio. A seguir, aplica-se o sinal de um gerador de sinais às placas de deflexão horizontal do osciloscópio.
Efetuadas estas operações, faz-se variar a frequência do gerador de sinais até se obter uma circunferência ou uma elipse na tela.
Quando isso se consegue indica-nos que a frequência desconhecida do sinal é a mesma que a do gerador de sinais, se os dois sinais aplicados são senoidais.
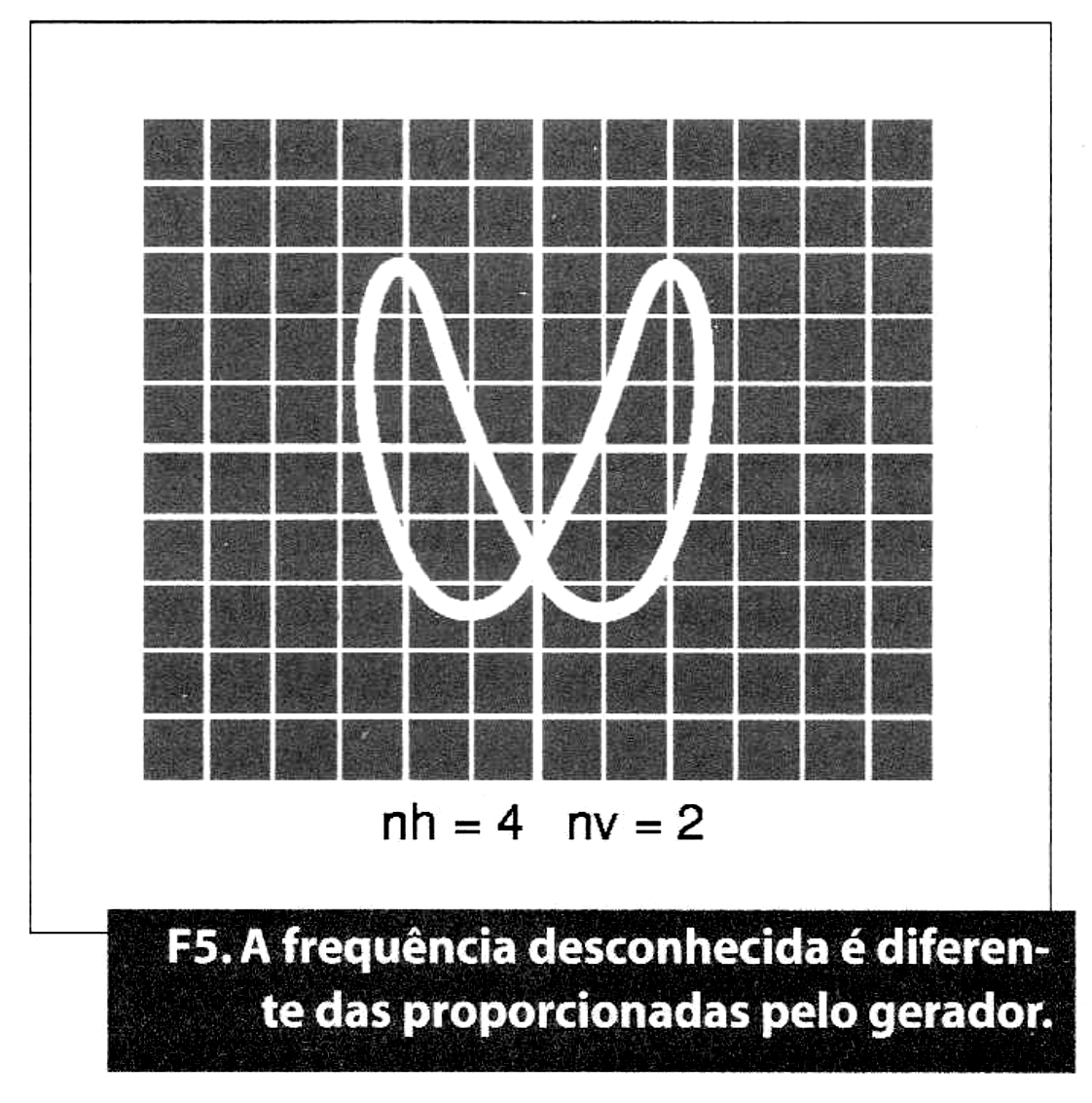
Se, com a gama de frequências do gerador de sinais não se conseguir a citada circunferência ou elipse é porque a frequência desconhecida é distinta das proporcionadas pelo gerador de sinais (figura 5).
Observando a imagem na tela, é possível deduzir a relação de frequências entre os dois sinais aplicados.
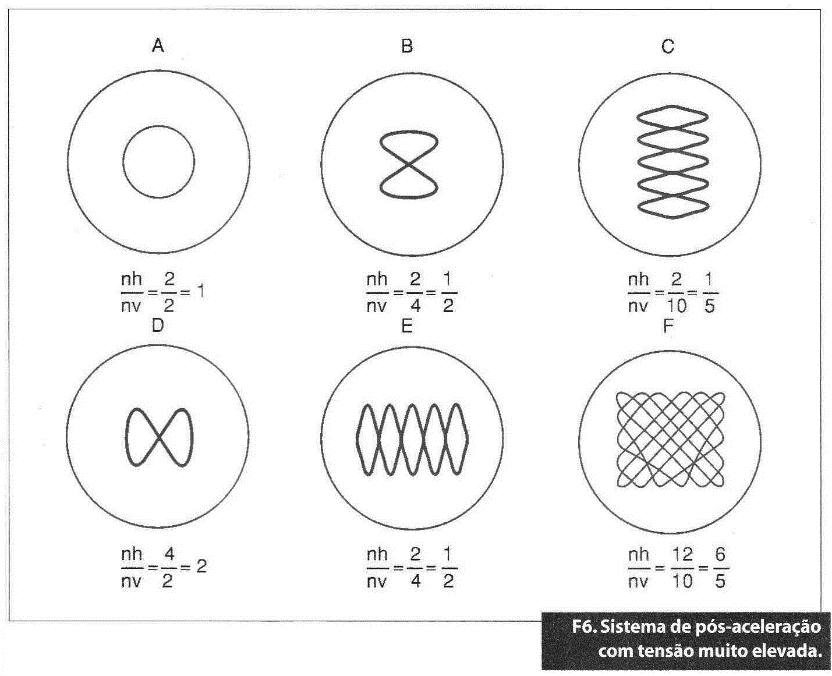
Na figura 6 mostram-se exemplos.
Para obter o valor da frequência desconhecida, basta contar o número de vezes que o traço cruza o eixo de simetria horizontal da tela, e dividi-lo pelo número de vezes que cruza o eixo de simetria vertical dela. O quociente é multiplicado pela frequência conhecida proporcionada pelo gerador de sinais, obtendo-se o valor da frequência desconhecida.
fx = fg nh/nv
onde:
fx é a frequência desconhecida;
fg é a frequência proporcionada pelo gerador de sinais;
nh é o número de vezes que o traço cruza o eixo de simetria horizontal da tela;
nv é o número de vezes que o traço cruza o eixo de simetria vertical da tela.
Por meio das figuras de Lissajous
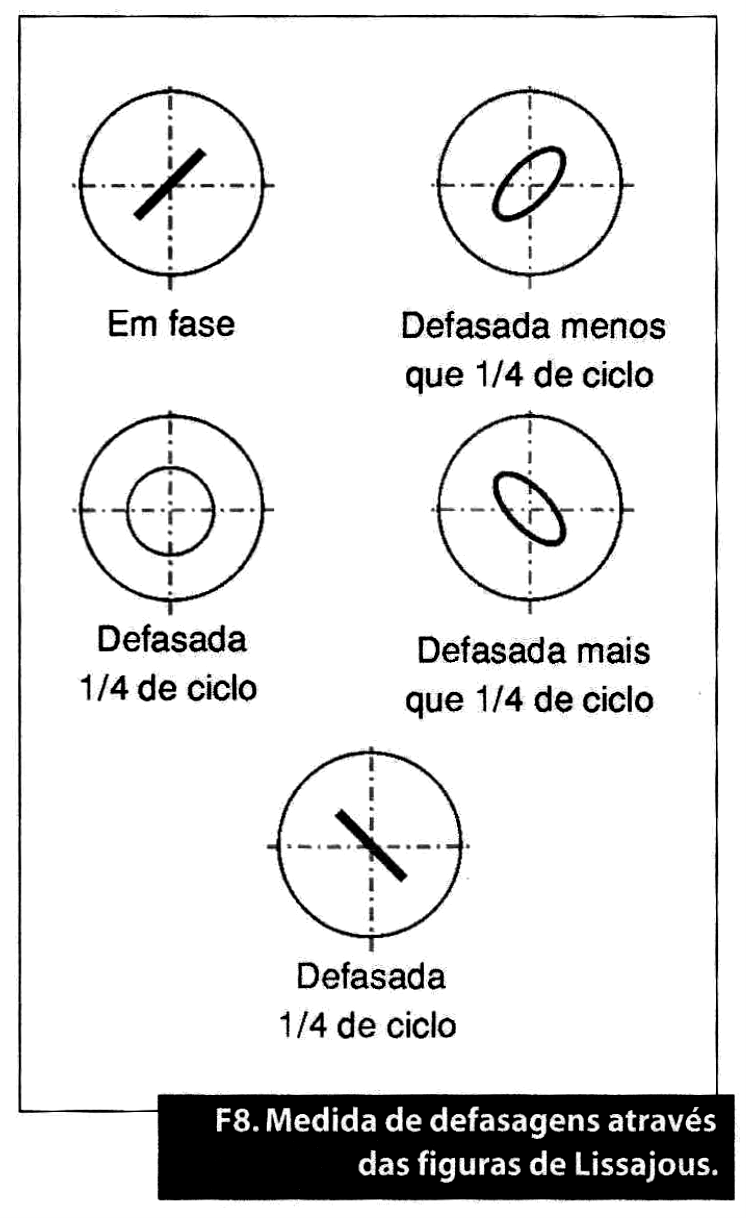
Tendo em conta que os sinais aplicados ao osciloscópio são da mesma frequência, na tela aparecerão círculos ou elipses com diferentes graus de excentricidade. A excentricidade da elipse na tela determina a defasagem entre os dois sinais analisados.

Na figura 8, mostram-se algumas imagens, nas quais se indicam os seus defasamentos. O osciloscópio no modo XY, permite-nos determinar rapidamente o desfasamento existente entre dois sinais.
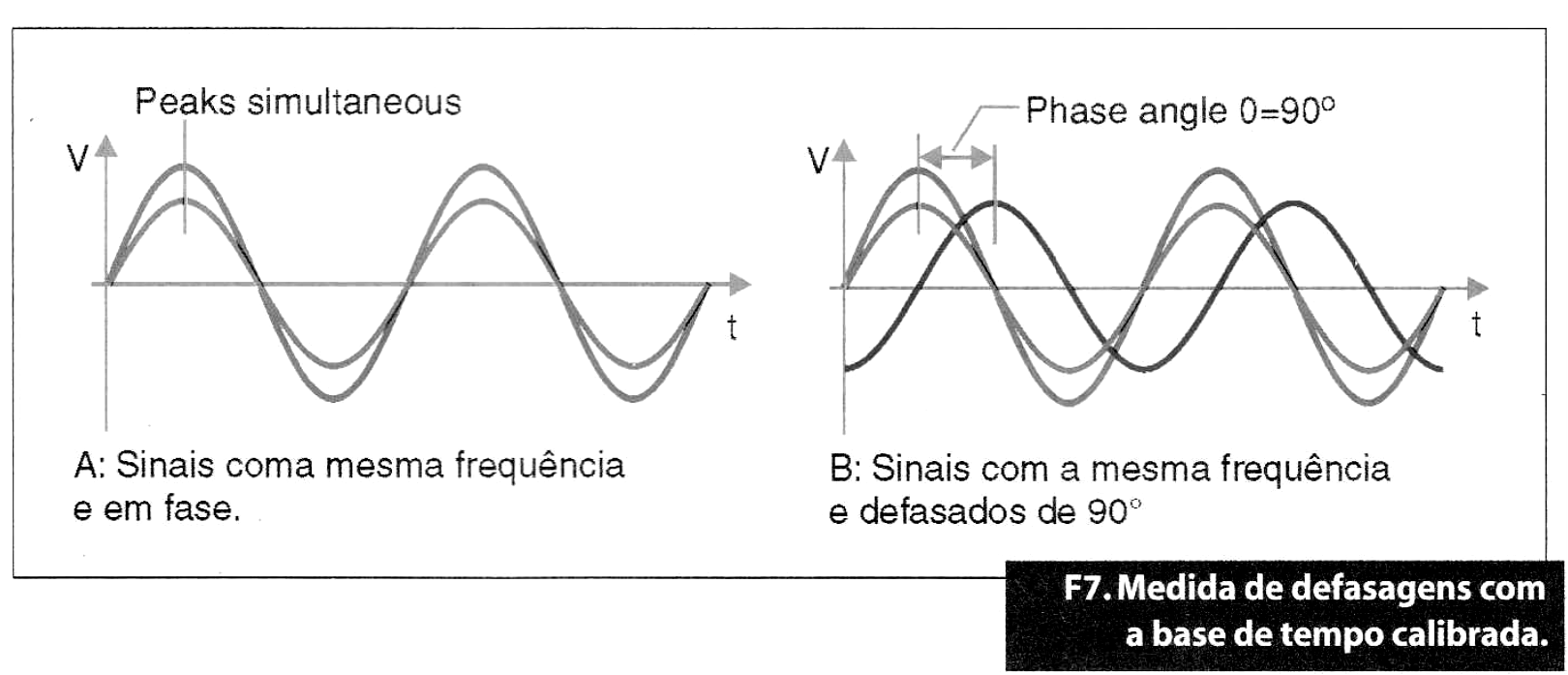
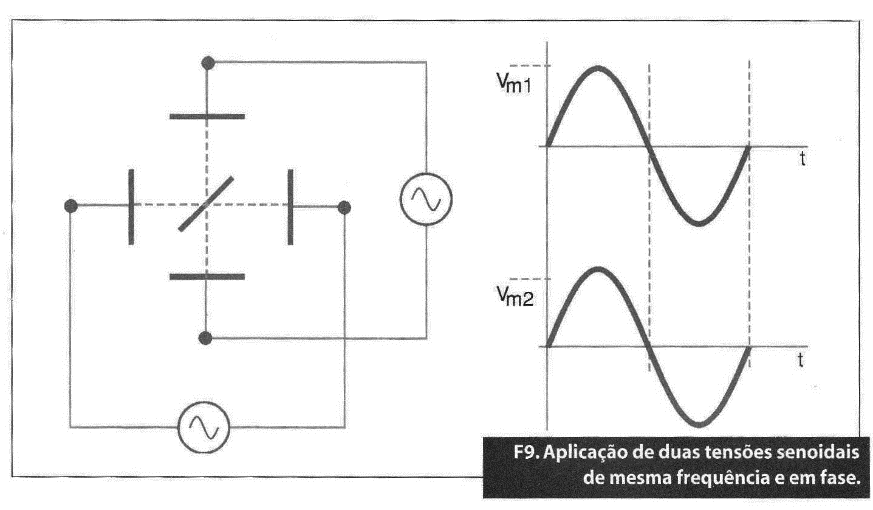
Aplicação simultânea de duas tensões alternadas senoidais da mesma frequência e em fase
A imagem que surge na tela é um traço oblíquo da direita para a esquerda e cuja inclinação depende da relação entre as amplitudes das tensões.
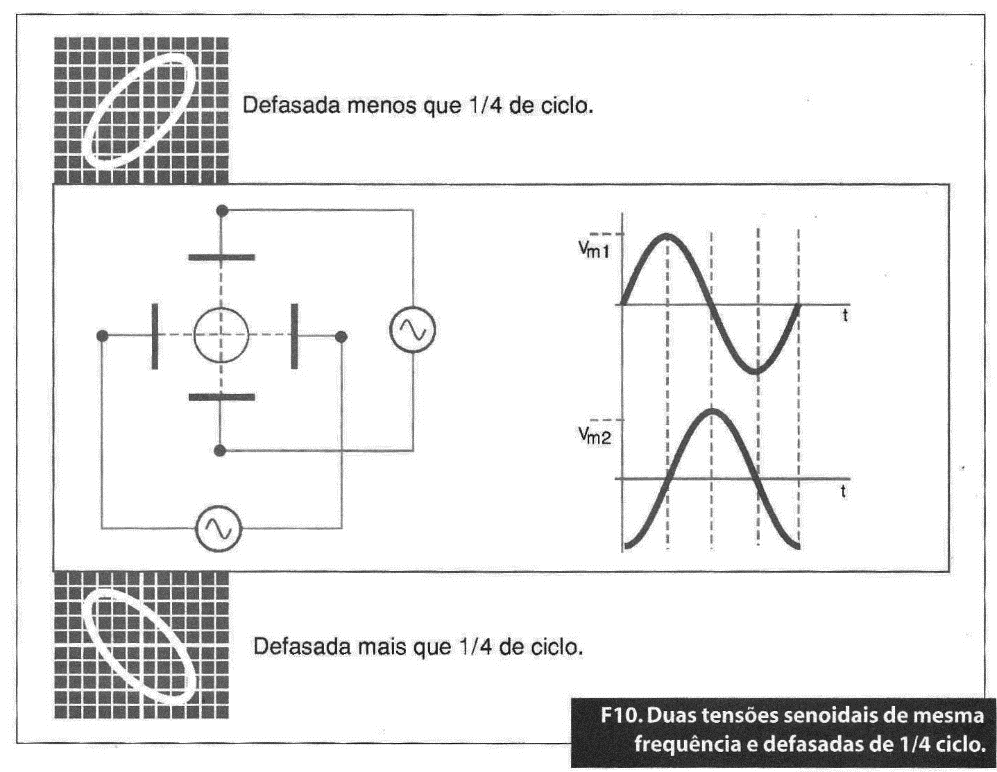
Aplicação simultânea de duas tensões alternadas senoidais da mesma frequência defasadas de 1/4 de ciclo
A imagem resultante é uma circunferência se as tensões forem da mesma amplitude. Sendo de amplitudes diferentes, a figura é uma elipse de eixo maior vertical ou horizontal conforme a tensão de maior amplitude for aplicada às placas verticais ou horizontais (figura 10).
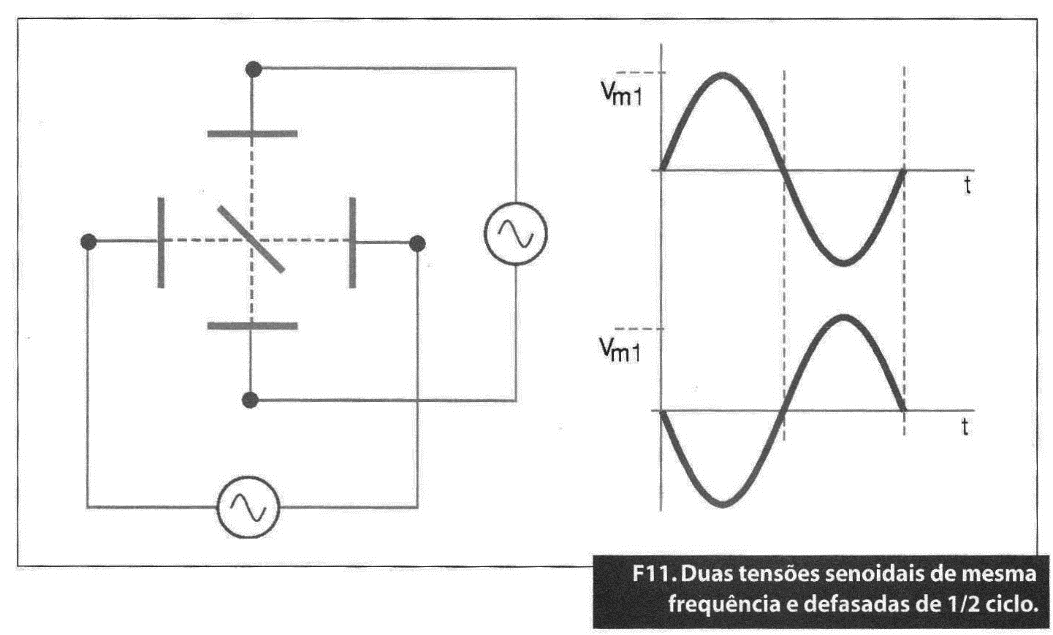
Aplicação simultânea de duas tensões alternadas senoidais da mesma frequência defasadas de 1/2 ciclo
Neste caso a figura que surge na tela é um traço oblíquo da esquerda para a direita, com uma inclinação de 45° se as tensões forem da mesma amplitude. Se forem de amplitudes diferentes, a inclinação poderá tomar valores entre 0° e 90° (figura 11).