Existem dispositivos mecânicos muito simples que, no entanto, se mal utilizados ou mal calculados podem levar a resultados inesperados bastante desagradáveis. Até mesmo um parafuso pode causar problemas se não soubermos exatamente como ele funciona. Sim, um simples parafuso segue leis físicas muito bem estabelecidas que, se não forem observadas podem trazer problemas. Veja neste artigo como "calcular" um parafuso.
O parafuso é uma "máquina simples" que encontra uma infinidade de usos. Ele não serve apenas para prender peças como muitos podem pensar, mas pode ser usado em configurações que transmitem força e movimento, conforme veremos a seguir.
Como máquina simples o parafuso permite um ganho de força ou "vantagem mecânica" e por isso pode ser usado em aplicações que vão muito além do que manter peças unidas.
O parafuso pode ser considerado uma modificação do plano inclinado. Se cortarmos uma peça de papel em forma de triângulo, que representa um plano inclinado, e a enrolarmos num lápis, conforme mostra a figura 1, teremos uma idéia muito clara de como funciona e se obtém um parafuso.
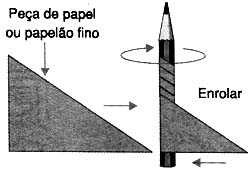
A distância entre os pontos em que cada volta do parafuso passa determina o "passo" do parafuso, ou se adotarmos o termo em inglês muito comum, o "pitch" do parafuso.
Girando o lápis em que o papel foi enrolado e preso, vemos que à medida que isso ocorre temos um movimento das espiras enroladas numa determinada direção, conforme mostra a figura 2.
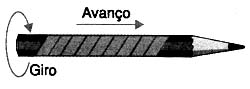
Observe que podemos associar esse movimento que as espiras fazem pode ser associado ao movimento de rotação do parafuso. Isso nos permite usar o parafuso para converter um movimento rotativo num movimento linear! Uma outra aplicação importante desta máquina simples.
O passo, que é determinado pela inclinação do plano que forma o parafuso, juntamente com seu diâmetro determina a vantagem mecânica que podemos obter além de outras características importantes.
Assim, conforme mostra a figura 3 para obtermos um parafuso, basta gravar num tubo de metal sólido os sulcos que tenham uma determinada inclinação que determine seu passo.
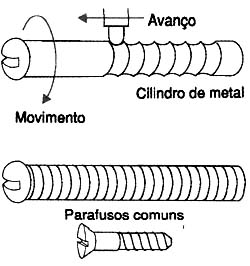
Evidentemente, a distância entre os sulcos e portanto o passo deve ser sempre constante.
Cálculos
Uma idéia de como podemos fazer alguns cálculos interessantes a partir da idéia do parafuso é a que nos dá o macaco, mostrado na figura 4.
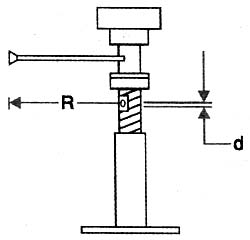
O que temos neste caso é a união de uma alavanca a um parafuso de modo a multiplicarmos a força que faz a alavanca se movimentar num percurso circular de modo que ela atue linearmente levantando um peso.
Se considerarmos que o braço da alavanca usada no macaco tem um comprimento R, podemos afirmar que no percurso de uma volta a sua extremidade, onde a força é aplicada percorre uma distância dada por:
D = 2 x p x R
Ao mesmo tempo, em uma volta o parafuso "avança" a distância correspondente a um passo. Se considerarmos on tamanho do passo "d", a vantagem mecânica, ou seja, "por quanto a força F fica multiplicada" será dado por:
V.M. = 2 x p x R/ d
Um exemplo prático nos mostra como um parafuso pode "aumentar" enormemente a força:
Suponhamos um macaco em que o comprimento do braço da alavanca seja de 50 cm e que o passo do parafuso seja de 0,5 cm. Essa alavanca multiplicará a força aplicada por:
V.M. = 2 x 3,14 x 50/0,5
V.M. = 6,28 x 100
V.M. = 628
Precisamos de uma força de apenas 1 N para levantar um "peso" de 628 N.
Temos ainda a vantagem de poder transformar um movimento giratório num movimento linear.
Um exemplo prático de dispositivo simples que pode ser elaborado segundo o princípio do parafuso é o atuador linear mostrado na figura 5.
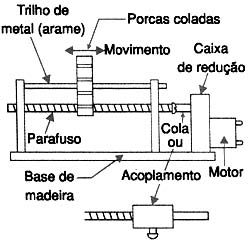
Usando uma caixinha de redução e um parafuso comprido (pelo menos 4" x 1/8") e uma porca, podemos montar um dispositivo simples capaz de movimentar peças linearmente com grande força.
Força pode ser calculada a partir do torque aplicado parafuso e o tamanho de seu passo.
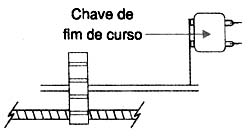
Uma opção para termos um atuador mais complexo seria colocar duas chaves de fim de curso nas extremidades do parafuso, conforme mostra a figura 6, de modo a desligar o motor quando a porta chegasse a esses pontos, não forçando assim a estrutura do atuador.
Uma outra aplicação prática é a prensa, como a mostrada na figura 7 e que pode produzir enormes forças, graças à vantagem mecânica do parafuso.

Conclusão
Veja que é importante saber como fazer esses simples cálculos com parafusos pois eles podem ajudar a elaborar dispositivos de grande utilidade nos projetos de mecatrônica.
Muito mais do que simplesmente segurar partes de modo fixo, o parafuso é uma máquina simples que pode ser usado de forma dinâmica transmitindo força e movimento!



















