Você sabia que qualquer sinal eletrônico, por mais que pareça ter uma forma de onda complicada, pode ser obtido através da soma de vários geradores de tensão senoidal? Essa descoberta, publicada pela primeira vez em 1822, foi utilizada como base para diversas outras descobertas nos ramos eletroeletrônicos. Vejamos como isso é possível.
Ondas, ondas e mais ondas
Jean Baptist Joseph Fourier (1768 — 1830), foi um grande estudioso dos mecanismos físicos de propagação do calor. Ao supor que o calor em um corpo qualquer se propaga através de ondas, Fourier desenvolveu uma matemática que caiu como uma luva para qualquer representação de fenômenos elétricos, pois estes também fazem uso de ondas. Seu trabalho Thèorie Analytique de La Chaleur, de 1822, mostrou ao mundo como era possível decompor qualquer onda em soma de senos e cossenos, através do que viria a se tornar conhecido como Série de Fourier.
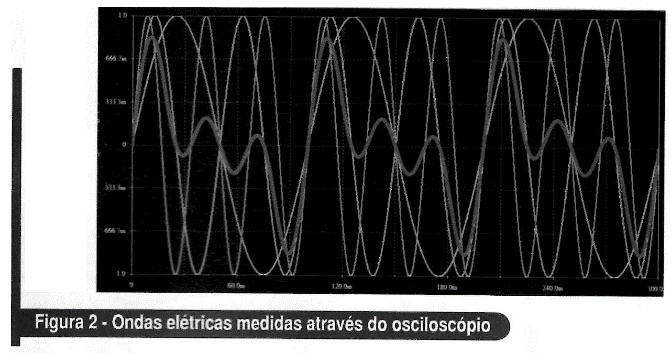
Para entender como isso é possível, vamos a um exemplo: o que acontece quando conectamos três geradores de onda senoidal em paralelo e aplicamos isto a uma carga? Neste exemplo ajustamos cada um deles para a mesma amplitude e fase, mas colocamos frequências diferentes. A carga receberá o resultado da soma das tensões enviadas por cada um dos geradores. A figura 1 exemplifica essa ideia e o resultado gráfico é mostrado na figura 2. Veja que o sinal azul resultante não tem o comportamento senoidal, formando uma outra onda, que nada mais é do que a soma em cada instante de tempo, dos níveis de tensão dos três geradores.
O que Fourier conseguiu perceber e demonstrar com seu teorema matemático é que se os valores de tensão, fase e frequência de cada um dos geradores forem ajustados coerentemente, a onda azul pode assumir qualquer formato desejado. Quanto maior o número de geradores ligados em paralelo, mais o sinal azul se aproxima do formato exato desejado. A precisão entre o formato que se quer e o sinal obtido estará ligado ao número de geradores montados em seu circuito.
Os coeficientes da Série de Fourier
Mas como saber quais os valores de tensão, frequência e fase a ajustar em cada gerador? Aí começa a genialidade de Fourier. O sinal azul pode ser escrito como uma função matemática f(x). Fourier demonstrou que qualquer que seja o f(x), ele pode ser escrito a partir da expressão abaixo:
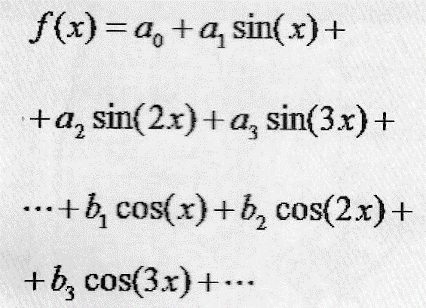
Cada uma destas letras da função representa um coeficiente da Série de Fourier. Em nosso circuito o valor de a0 é equivalente a uma componente DC, ou seja, ligar uma bateria DC em paralelo aos geradores AC.
O valor de a1 é equivalente à tensão ajustada no gerador A1, que tem fase zero (seno) e frequência x (por exemplo, 10 Hz).
O valor de a2 é equivalente a tensão ajustada no gerador A2, que tem fase zero (seno) e frequência 2x (seguindo o exemplo: 20 Hz), e assim por diante em todos os geradores de senoides (fase zero).
Faltam ainda as letras "b": O valor de b1 é equivalente a tensão ajustada no gerador 131, que tem fase 90° (cosseno) e frequência x (10 Hz). O valor de b2 é equivalente a tensão ajustada no gerador B2, que tem fase 90° (cosseno) e frequência 2x (20 Hz), e assim por diante em todos os geradores de cossenóides (fase 90°.
Assim, para obter qualquer formato de onda é necessário descobrir quais são os valores de a0, a1, a2, a3, a4.... b1, b2, b3, b4, ... adequados.
Através do cálculo integral e diferencial, Fourier chegou a equações que permitem calcular estes coeficientes para qualquer sinal. As expressões utilizadas em cada um deles são mostradas a seguir:
Cálculo da componente DC (a0):
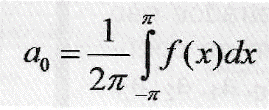
Cálculo das componentes cossenoides (a1, a2, a3, a4 ...):
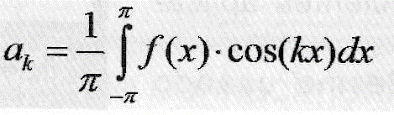
Cálculo das componentes senoidais (b1, b2, b3, b4 ...):
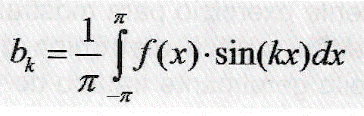
Uma vez que forem obtidos estes coeficientes, basta montar nossos circuitos e fazer os testes.
Exemplos
Para ilustrar a quão poderosa é essa ferramenta matemática, serão apresentados três exemplos de ondas obtidas através da Série de Fourier. O procedimento é sempre o mesmo: coloca-se o f(x) do sinal nas equações dos coeficientes, calcula-se os valores de a0, a1, a2, a3, a4 b1, b2, bv3, b4, adequados e ajusta-se tantos geradores quanto for a precisão desejada.
1.Onda quadrada
Após os cálculos dos coeficientes obteve-se:
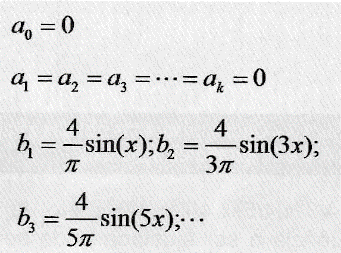
Note que apenas os geradores b1, b2, b3, b4, ... precisarão ser ligados, com os respectivos ajustes de tensão: 4/π, 4/3π, 4/5π, 4/7π, 4/9π e, etc. Já a frequência a ser ajustada pode ser, respectivamente: 10 Hz, 30 Hz, 50 Hz, 70 Hz, 90 Hz, etc. Todos deverão estar em fase zero, ou seja, gerando senoides.
Fizemos a montagem dos circuitos com 4 (onda azul), 8 (onda vermelha) e 16 (onda lilás) geradores. O resultado é mostrado na figura 3.

2.0nda triangular
Após os cálculos dos coeficientes obteve-se:
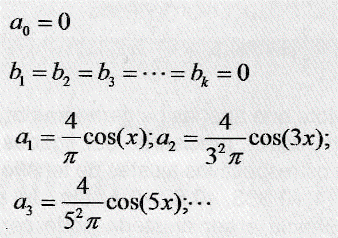
Note que apenas os geradores a1, a2, a3, a4, ... precisarão ser ligados, com os respectivos ajustes de tensão:
4/π, 4/32π, 4/52π, 4/72π, 4/92π, etc. Já a frequência a ser ajustada pode ser, respectivamente: 10 Hz, 30 Hz, 50 Hz, 70 Hz, 90 Hz, etc. Todos deverão estar em fase 90°, ou seja, gerando cossenóides.
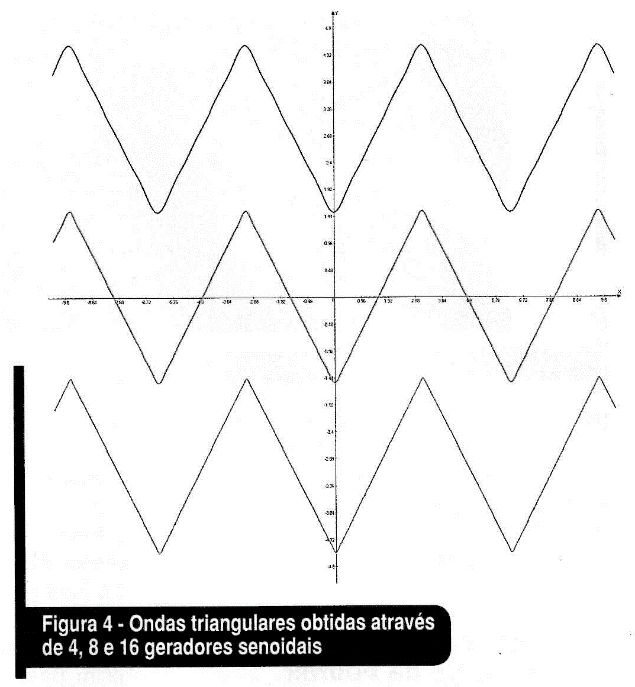
Fizemos a montagem dos circuitos com 4 (onda azul), 8 (onda vermelha) e 16 (onda lilás) geradores. O resultado é ilustrado na figura 4.
3. Onda "dente de serra"
Após os cálculos dos coeficientes obteve-se a equação abaixo:
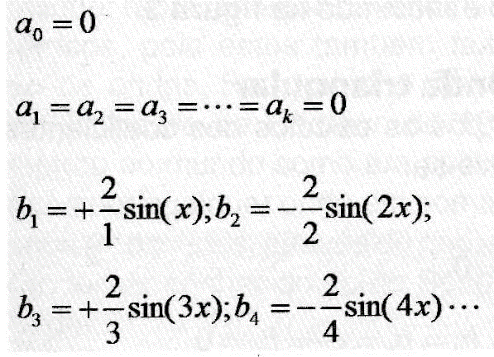
Note que apenas os geradores b1, b2, b3, b4, ... precisarão ser ligados, com os respectivos ajustes de tensão: +2, -1, +0,333, -0,5, +0,4, etc. Já a frequência a ser ajustada pode ser, respectivamente: 10 Hz, 20 Hz, 30 Hz, 40 Hz, 50 Hz, etc. Todos deverão estar em fase zero, ou seja, gerando senoides.
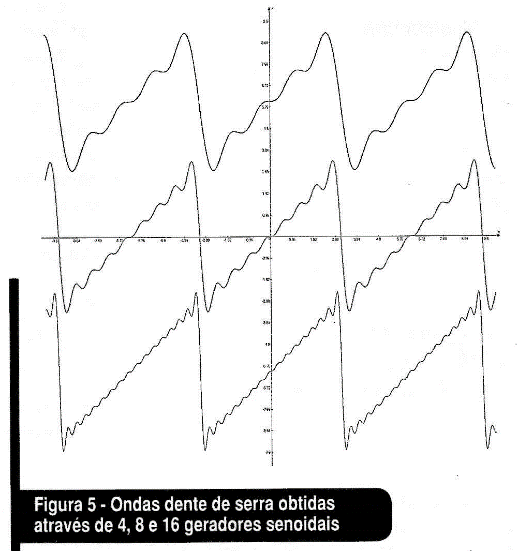
Fizemos a montagem dos circuitos com 4 (onda azul), 8 (onda vermelha) e 16 (onda lilás) geradores. O resultado é exibido na figura 5.
Conclusão
Apesar dos exemplos mostrados não utilizarem os coeficientes a0, a1, a2, a3, a4 ... isto não é regra. Cada sinal deve ser analisado e calculado para obter todos os coeficientes aplicáveis. Mesmo usando uma matemática mais avançada, necessitando de conhecimentos de cálculo integral e diferencial, as Séries de Fourier consistem em um excelente exercício para mostrar uma aplicação prática eletrônica de um conceito geralmente tratado de forma abstrata no curso superior.