Quem não se lembra de um dos nossos projetos de maior sucesso, o Micro Transmissor de FM que saiu na Revista Saber Eletrônica 56 de março de 1977? Este transmissor tinha um diferencial. A bobina do circuito era impressa na própria placa que foi dada de brinde na capa da revista. Neste artigo explicamos o modo como chegamos a essa bobina, ensinando como calcular uma bobina impressa numa placa.
Para os que desejarem lembrar deste transmissor, recomendamos o nosso vídeo da série Artigos e Vídeos que Marcaram época VAM001 e se quiserem fazer a montagem, o Micro Transmissor de FM II (ART2801). Micro Transmissor de FM (ART2935) e Micro Transmissor de FM (ART2803).
Começamos por lembrar da capa da revista que muitos ainda têm em sua coleção, dada a figura 1.

Na figura 2, mostramos a placa de circuito dada como brinde onde se destaca a bobina impressa e a montagem de um trimmer de porcelana como se usava na época, do outro lado.
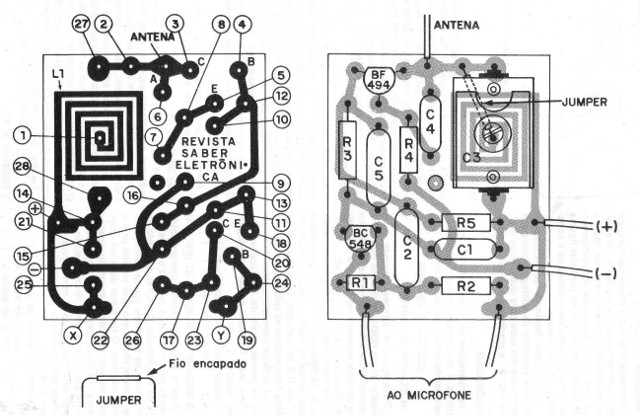
Conforme relato num vídeo histórico, a dificuldade maior que tive foi dimensionar essa bobina para que ela desse a cobertura da faixa de FM. Mas, calcular a indutância de uma bobina impressa não é tão difícil para quem domina um pouco da matemática.
Na verdade, hoje temos as calculadoras, inclusive on-line que permitem realizar cálculos com fórmulas que tenham expoentes fracionários, funções trigonométricas, com certa facilidade.
Calculando a bobina
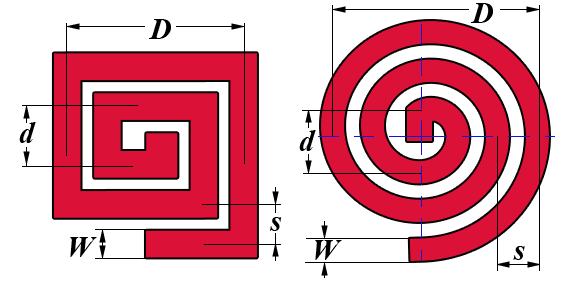
Na figura 3 temos dois padrões básicos que podem ser usados nos cálculos. As diferenças obtidas com os procedimentos, podem variar em torno de 3% o que é bastante bom para a maioria das aplicações. Veja que essas bobinas também podem variar de forma, passando de padrões como o quadrado, para o pentágono, hexágono e mesmo com mais lados.
Uma primeira fórmula que encontramos e que exige uma boa calculadora científica, pois vamos trabalhar com potências negativas ou fracionárias é:
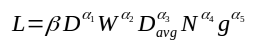
Esta fórmula foi obtida de uma documentação que analisou uma base de dados de indutores.
Nela temos:
L é a indutância em nanohenry (nH)
D é o diâmetro externo da bobina em micrometros (um)
W é a largura da trilha na placa de circuito impresso em micrometros (um) – veja figura 3 - (*)
Davg = diâmetro médio da bobina em micrometros (veja figura 3)
N = número de espiras ou voltas da bobina
G = s – W – espaço entre as espiras em um (veja figura 3 como é tomada esta dimensão)
Α e β são constantes que dependem do layout da bobina, dadas pela seguinte tabela:
| Layout | β | α1 | α2 | α3 | α4 | α5 |
| Quadrado | 1.62·10-3 | -1.21 | -0.147 | 2.40 | 1.78 | -0.03 |
| Hexagonal | 1.28·10-3 | -1.24 | -0.174 | 2.47 | 1.77 | -0.049 |
| Octogonal | 1.33·10-3 | -1.21 | -0.163 | 2.43 | 1.75 | -0.04 |
(*) Lembramos que 1 um = 10-6 m.
Uma segunda fórmula que encontramos em documentação técnica é derivada de princípios do eletromagnetismo e que roda também em sites é:
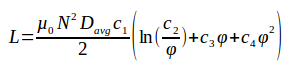
Nessa fórmula:
L é a indutância em microhenry (uH)
μo = constante magnética que equivale a 4π x 10-7 ou 1,2566 x 10-6 H/m
N = número de espiras
Davg = diâmetro médio da bobina (um) - (ver fórmula anterior)
Φ = Fator de enchimento – Ver fórmula mais adiante
C (1 a 4) – fatores da tabela que dependem do formato da bobina
| Layout | c1 | c2 | c3 | c4 |
| Quadrada | 1.27 | 2.07 | 0.18 | 0.13 |
| Hexagonal | 1.09 | 2.23 | 0.00 | 0.17 |
| Octogonal | 1.07 | 2.29 | 0.00 | 0.19 |
| Circular | 1.00 | 2.46 | 0.00 | 0.20 |
Esta fórmula tem boa precisão quando a relação s/W se mantém pequena. Quando ela aumenta, a precisão dos valores obtidos diminui. No geral, é garantida uma precisão melhor que 8%.
O chamado fator de enchimento, indica quando a bobina é “vazia” em seu interior, pode ser calculado pela fórmula:
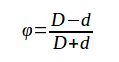
Φ = fator de enchimento
D = diâmetro externo da bobina
d = diâmetro interno
Veja que os diâmetros não têm unidade. Basta manter os dois na mesma unidade de modo a se obter um número adimensional.
Outro ponto importante a ser considerado é o fator de qualidade (Q) que tem seu melhor valor quando a bobina é circular e a relação s/D = 4.
Fórmulas adicionais
O cálculo da indutância que deve ter a bobina impressa parte de outros cálculos, mas o que temos é a frequência ou a faixa de frequências em que o circuito deve operar.
Assim, no nosso caso do transmissor de FM, por exemplo, precisamos calcular que indutância deve ter a bobina quando em paralelo com um trimmer comum, por exemplo de 3 – 20 pF como se usava na época possamos cobrir a faixa de FM, 88 a 100 MHz. (figura 4)

Assim, fixamos em nosso cálculo da indutância o capacitor na metade de sua capacitância (10 pF), valor que era facilmente alcançado pela maioria dos tipos existentes no mercado na época, e a frequência em 100 MHz, aplicando a fórmula para capacitância em picofarads e indutância em microhenry:
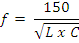
A frequência será obtida em MHz.
Veja mais em: https://www.newtoncbraga.com.br/index.php/matematica-para-eletronica/2163-m127.html
Assim, aplicando essa fórmula, obtemos que a indutância a ser usada nos cálculos será:
L = 0,253302 uH (Valor aproximado)
Na internet encontramos uma útil calculadora para circuitos LC que pode ser de grande utilidade para os leitores que estão projetando um circuito com bobina impressa, usando os procedimentos descritos.
https://goodcalculators.com/resonant-frequency-calculator/
Com esse valor, determinamos o número de voltas para a bobina que foi impressa na placa-brinde, com sucesso.
Encontramos um valor intermediário entre 5 e 6 espiras que nos atendeu perfeitamente com o projeto indicado.
E, para bobinas desse tipo hoje, além do calculador do circuito LC podemos encontrar na internet um calculador muito útil para o número de espiras:
https://coil32.net/online-calculators/pcb-inductor-calculator.html
Assim, se você está desenvolvendo seu projeto com base em bobinas impressas, os procedimentos que demos podem ser úteis, mas cuidado.
Bobinas impressas estão normalmente elaboradas em placas feitas de materiais que possuem propriedades elétricas específicas. Quando trabalhamos com frequências relativamente baixas, não temos problemas, mas em frequências muito altas ou mesmo com materiais como a fenolite que pode absorver umidade, podemos ter problemas.
No caso do microtransmissor, realmente vimos que em alguns casos, as placas dadas como brinde na revista ficaram expostas a umidade e isso fez com que em alguns projetos o circuito não oscilasse. Nossa recomendação foi deixar a placa em lugar seco por algum tempo ou mesmo num ambiente com silica gel. Com as placas de fibra modernos, o problema quase inexiste.
As fórmulas e procedimentos que damos derivam da fórmula de Wheler que abordamos em artigo de nosso site, e que é a mais conhecida. O link é: https://www.newtoncbraga.com.br/index.php/matematica-na-eletronica/6071-m252.html?highlight=WyJ3aGVsZXIiXQ==
É claro que os cálculo que mostramos são empíricos, ou seja, partem de fórmulas aproximadas que funcionam com boa tolerância dentro de uma certa margem de valor. Se os nossos seguidores querem um procedimento mais exato, por exemplo, para um trabalho acadêmico, sugerimos consultar a seguinte documentação.
https://ietresearch.onlinelibrary.wiley.com/doi/pdf/10.1049/iet-pel.2018.5780




















