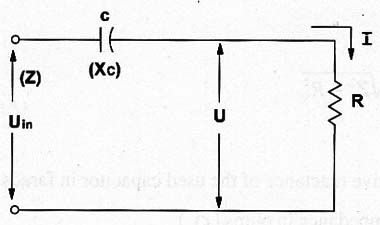
A reatância capacitiva de um capacitor pode ser usada num divisor de tensão, possibilitando o projeto de fontes sem transformador, como a mostrada na figura 1. Supondo uma carga resistiva, podemos calcular R e C usando as seguintes fórmulas.
Fórmula 1
Calculatndo R:
R = U / I
Onde : U é a tensão na carga em volts (V)
I é a corrente na carga em ampères (A)
R é a resistência de carga em ohms (Ω)
Obs: U e I são valores RMS (valores médios quadráticos)
Fórmula 2
Impedancia:
Z = Uin / I
Onde : Z é a impedância do circuito em ohms (Ω)
Uin é a tensão de entrada em volts (V)
I é a corrente total de carga em ampères (A)
Fórmula 3
Reatância capacitiva:
Xc = √(Z2 - R2)
Onde: Xc é a reatância capacitiva do capacitor usado em ohms (Ω)
Z é a impedância do circuito em ohms ( Ω)
R é a resistência de carga em ohms (Ω)
Fórmula 4
C = 106 / (2 x Π x f x Xc)
Onde : C é a capacitância em microfarads (uF)
Π vale 3,1416
f é a frequência da linha de alimentação em hertz (Hz)
Xc é a reatância capacitiva em ohms (Ω)
Exemplo de Aplicação:
Determina a capacitância de C no circuito da figura 2 para alimentar uma lâmpada de 12 V com 50 mA a partir da rede de 117 V x 60 Hz.
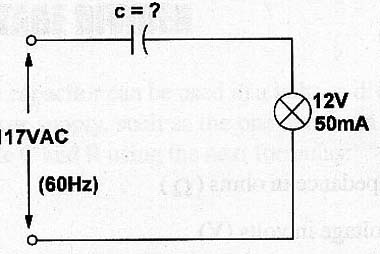
Dados U = 12 V
Uin = 117 V
I = 0.02 A (20 mA)
f = 60 Hz
C = ?
a) Calculando R (formula 1)
R = 12 / 0.02 = 600 Ω
b) Determinando Z (formula 2)
Z = 117 / 0.02 = 5 850 Ω
c) Agora, Xc pode ser calculado usando a fórmula 3
Xc = √( (5.880)2 – (600)2 )
Xc = √( (31,9 x 106) – (0,36 x 106) )
Xc = √( 31,5 x 106 )
Xc = 5 618 Ω
d) Encontrando C (fórmula 4):
C = 106 / (2 x 3,14 x 60 x 5,618)
C = 106 / (2.116 x 106)
C = 1 / 2.116
C = 0.47 µF or 470 nF


















