Fundamental na medida de diversas grandezas elétricas como resistências, capacitâncias, indutâncias, etc. a ponte de Wheatstone consiste num circuito sensível que pode ser facilmente implementado e usado. Veja neste artigo o que é a ponte de Wheatstone e como utilizá-la. Daremos também alguns projetos práticos interessantes para os iniciantes que desejam utilizar este circuito.
Os dos problemas que ocorre quando introduzimos num circuito um instrumento para realizar uma medida é que este instrumento afeta a grandeza que está sendo medida.
Por exigir uma certa corrente para funcionar, o instrumento é responsável “pelo desvio” de parte da energia envolvida no processo e, com isso, ocorre uma alteração sensível.
Um exemplo simples pode ser visto no circuito da figura 1.
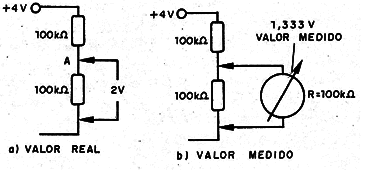
Neste circuito, na realidade a tensão no ponto A é a metade da tensão na entrada, ou seja, devemos ter 2 V.
No entanto, com a introdução de um instrumento que tenha certa resistência interna e que, portanto, desvie energia, cai a resistência total no ramo medido e cai também a tensão no ponto A.
Medimos então um valor muito menor do que os 2 V esperado.
Uma maneira interessante de se usar um instrumento de medida sem que ocorra este problema é fazendo uso de uma ponte.
Uma ponte consiste basicamente num circuito com 4 braços, arranjados de tal forma que podemos aplicar uma tensão e detectar seu equilíbrio, o que ocorre quando os valores dos componentes dos braços estiverem com uma certa relação de valores.
Nestas condições, a corrente no instrumento será nula, conforme mostra a figura 2.
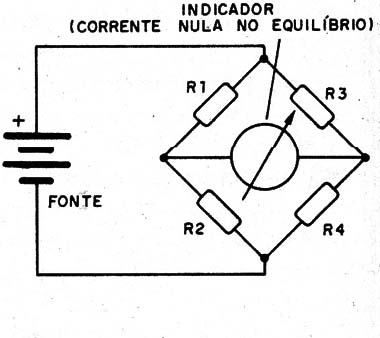
Conhecendo o valor de 3 componentes da ponte, podemos facilmente calcular o quarto no momento em que conseguirmos o ponto de nulo.
O tipo mais conhecido de ponte é a de Wheatstone, em homenagem ao seu criados.
Esta ponte é usada para a medida de resistências.
A Ponte de Wheatstone
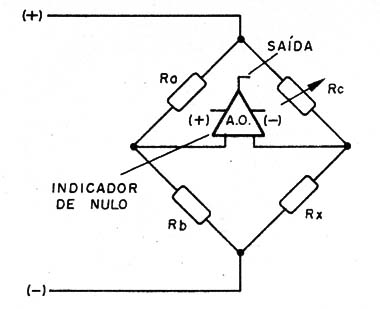
Na figura 3 temos a configuração básica da ponte de Wheatstone.
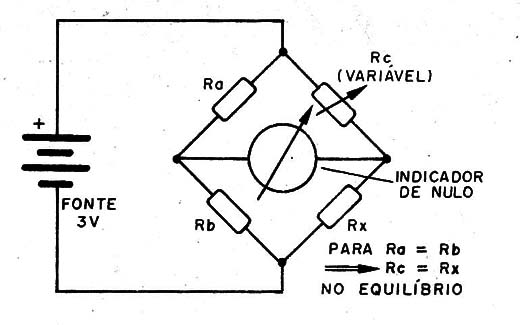
Os resistores Ra e Rb seguem uma relação de valores que depende das resistências que desejamos medir.
Para efeito prático, facilitando nossas explicações, podemos fazer Ra = Rb.
Rc é um resistor variável e Rx é o resistor cuja resistência pretendemos medir.
Na entrada da ponte aplicamos uma tensão contínua e na sua parte central, na junção dos quatro elementos, ligamos um detector de nulo, que pode ser qualquer tipo de detector de corrente contínua, por exemplo, um microamperímetro, uma lâmpada, etc.
Para maior sensibilidade, o ideal é ligar um microamperímetro, se bem que na parte prática deste artigo, ensinaremos como usar circuitos adicionais que aumentam a sensibilidade.
O funcionamento deste sistema é o seguinte, partindo do caso em que usamos um microamperímetro como detector de nulo.
É fácil observar pela figura 4 que, para que não circule corrente alguma pelo circuito indicador, é preciso que a tensão no ponto A seja igual ao ponto B.
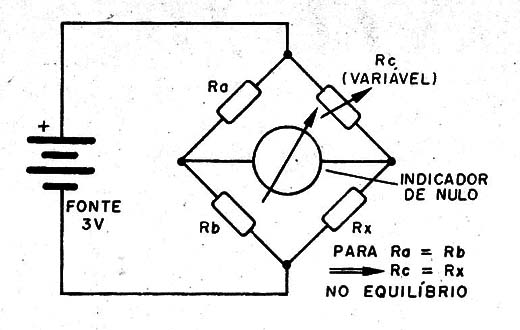
Se a tensão do ponto A for maior do que a tensão no ponto B, a corrente circula de A para B.
Se a tensão do ponto A for menor do que a tensão no ponto B, a corrente circula de B para A.
As correntes serão tanto maiores quanto maiores forem sãs diferenças entre as duas tensões.
Portanto, para que as tensões A e B sejam iguais, e com isso não haja corrente circulando, basta que Ra seja igual a Rb e que Rc seja igual a Rx.
Uma proporção entre eles que pode ser expressa pela fórmula:
Ra/Rb = Rc/Rx
Esta fórmula pode ser facilmente deduzida se considerarmos que Ra e Rb forma um divisor de tensão e que, Rc e Rx formam outro divisor de tensão.
Igualando as tensões nos divisores obteremos a relação indicada.
Como Ra e Rb são fixos, é fácil perceber que a relação se satisfaça e a corrente no instrumento indicador seja nula.
Quando isso acontece, dizemos que a ponte está em equilíbrio.
Tomemos um exemplo prático.
Na figura 5 temos uma ponte em que:
Ra = Rb = 1 k Ω
Rc = 10 k – potenciômetro
Rx = resistor de 2,2 k Ω
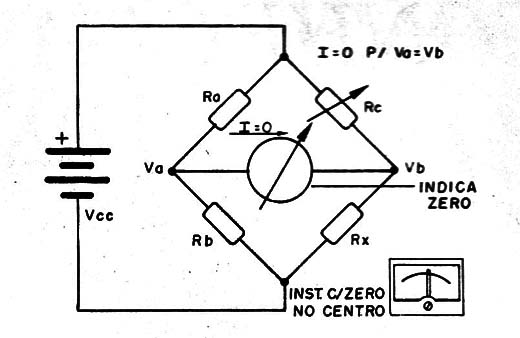
O indicador é um microamperímetro de 100 – 0 – 100 µA e a fonte de alimentação uma pilha de 1,5 V ou ainda duas pilhas de 1,5 V.
(Veja que na fórmula de equilíbrio ao aparece a tensão da fonte, o que significa que seu valor não influi no equilíbrio. A escolha da tensão para uma montagem prática depende apenas da sensibilidade d instrumento usado e da ordem de grandeza dos resistor medidos)
Colocando Rx no circuito e Re em qualquer posição, certamente não haverá equilíbrio e a corrente poderá circular no instrumento num sentido ou noutro.
Por isso, devemos usar um microamperímetro com zero no centro da escala para este tipo de montagem, conforme o tipo mostrado na figura 6.

Devemos então variar vagarosamente o valor de Rc, até que a corrente registrada pelo instrumento seja zero, ou seja, até o instante em que tenhamos conseguido o equilíbrio.
Quando isso ocorrer, no nosso caso, podemos dizer que a resistência ajustada em Rc é igual a resistência de Rx.
Se previamente tivermos colocado uma escala em Rc de modo a termos os valores de resistências para diversas posições do cursor, conforme mostra a figura 7, bastará ler o valor do resistor medido no próprio potenciômetro.
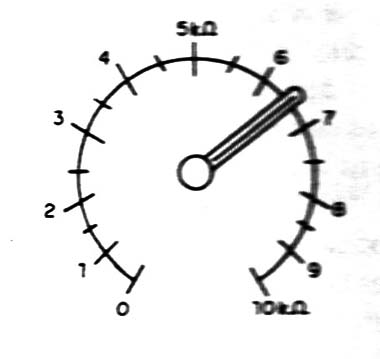
A precisão da medida obtida dependerá da precisão dos valores dos componentes usados, e também da indicação do instrumento.
Para um aperfeiçoamento maior, podemos colocar na nossa ponte uma chave seletora que nos permita trocar Rc, pois o valor deste componente limita a faixa de resistências que podemos medir.
Temos então um circuito como o da figura 8.
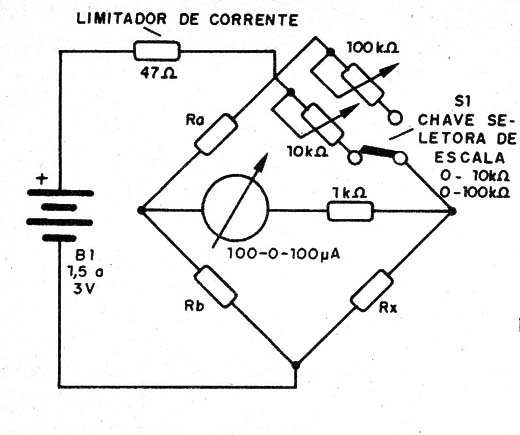
Outra possibilidade consiste em alterar o valor de Ra e Rb, mas temos ainda um problema prático a ser considerado.
Se a resistência de Rx for muito baixa, devemos também ajustar Rc para apresentar uma resistência e o resultado total será uma resistência muito pequena entre os pólos da fonte de alimentação.
Esta baixa resistência drenará da fonte uma corrente muito intensa que, tanto pode queimar os componentes (Rx e Rc) como também causar um curto circuito na fonte, conforme mostra a figura 9.
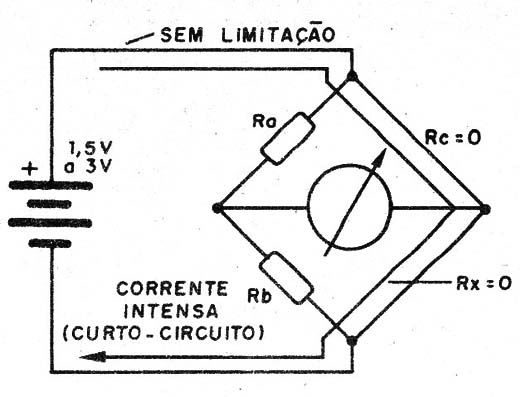
Outro problema será o próprio esgotamento da fonte, se ela for formada por pilhas.
Circuitos Práticos
Partindo dos circuitos que vimos, podemos contornar alguns problemas e elaborar projetos que podem ser de utilidade para os leitores.
O primeiro projeto é mostrado na figura 10.
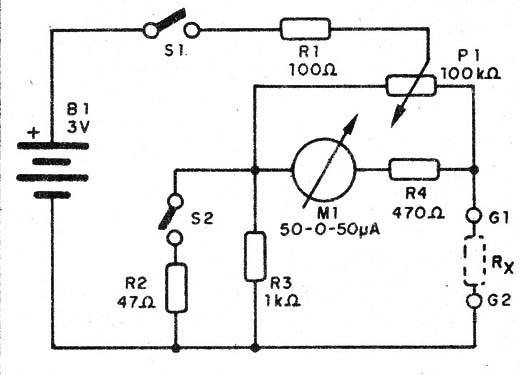
Este circuito usa como detector um microamperímetro com 0 no centro.
Um indicador de estado de bateria de antigos gravadores é um instrumento interessante para ser empregado com sucesso na montagem.
O resistor R serve de limitador de corrente para o caso da resistência Rx a ser medida ser muito baixa.
A chave S1 coloca num dos braços da ponte um resistor de baixo valor para medirmos pequenas resistências.
Na figura 11 temos o aspecto da montagem utilizando uma barra de terminais, já que os poucos elementos não justificam o uso de uma placa de circuito impresso.
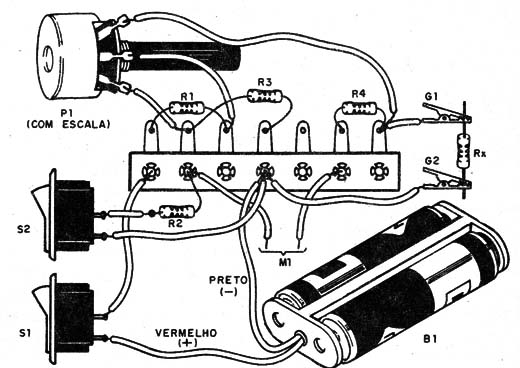
Para a conexão de Rx poderemos utilizar bornes ou garras e a calibração de P1 pode ser feita com base em resistores comuns com valores conhecidos.
Para usar a ponte é simples: basta ligar Rx e tentar o equilíbrio. Se não conseguimos o ajuste de P1 para o instrumento, fechamos S1.
Se ainda assim o ajuste não for possível, é sinal de Rx é maior do que 100 k Ω.
Para estender o alcance use para P1 um potenciômetro de 470 k ou mesmo 1 M e aumente B para 6 V. R1 deve ser alterado para 47 k Ω.
Outro projeto bastante sensível de ponte de Wheatstone faz uso de um sensível detector de nulo com operacional, conforme mostra a figura 12.
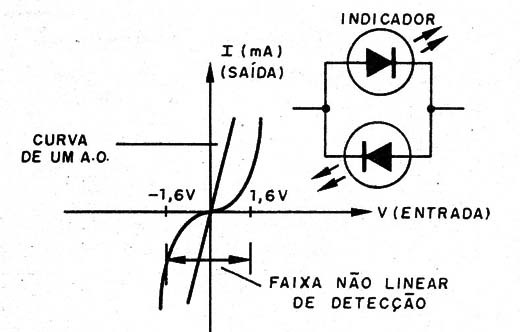
Um dos motivos pelos quais não podemos usar diretamente LEDs na configuração mostrada anteriormente é porque os LEDs precisam de pelo menos 1,6 V para acender.
Isso significa que a faixa de nulo detectada torna-se larga afetando a precisão, conforme mostra a figura 13.
Com a utilização de um amplificador operacional temos o seguinte princípio de funcionamento:
Na entrada inversora estabelecemos através de Ra e Rb uma tensão igual à metade da tensão de alimentação.
Se Rc for ajustado para ter o mesmo valor de Rx teremos também na entrada não-inversora uma tensão igual à metade da tensão de alimentação.
Ora, os amplificadores operacionais fornecem uma saída que depende da diferença entre as tensões de entrada, conforme mostra sua curva característica na figura 14.
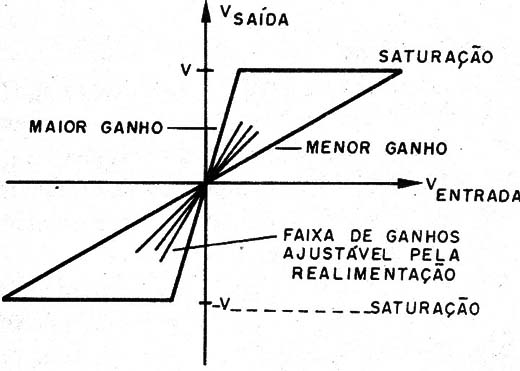
Se ligarmos dois LEDs em oposição a um divisor com dois resistores que estabeleça uma tensão igual à metade da tensão de alimentação, quando a situação acima ocorrer (equilíbrio) a corrente nos LEDs será nula e eles permanecerão apagados.
Veja então que se Rc for maior que Rx a tensão de saída do operacional será maior do que a tensão no divisor e com isso acende o LED1.
Por outro lado, se Rc for menor que Rx a tensão de saída será menor do que a tensão no divisor e com isso acende LED2.
O ganho de um operacional é muito grande, chegando a 100 000 vezes. O que significa que uma variação mínima de Rc no ajuste do equilíbrio já leva um ou outro LED a acender, pois a ponte se desequilibra facilmente.
Isso significa que usando todo o ganho do circuito, o equilíbrio da ponte se torna crítico.
Ficará muito difícil ajustar o ponto exato em que os dois LEDs apagam.
Poderemos resolver este problema controlando o ganho do operacional, o que se consegue através de um potenciômetro de realimentação.
Este potenciômetro é ligado entre a saída e a entrada inversora, conforme mostra a figura 15.
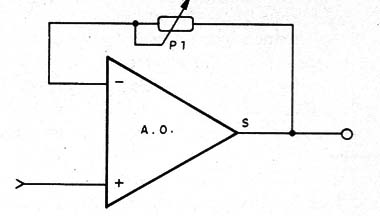
Reduzindo o valor da resistência do potenciômetro, o ganho do operacional tende a 1 e com isso temos maior facilidade em obter o ponto em que os LEDs apagam.
Depois, aumentando a resistência gradualmente, aumentamos o ganho e com isso estreitamos a faixa de ajuste, de modo a termos mais precisão, ou seja, fazemos um ajuste fino.
Tudo isso nos vela ao circuito final da ponte na figura 16.
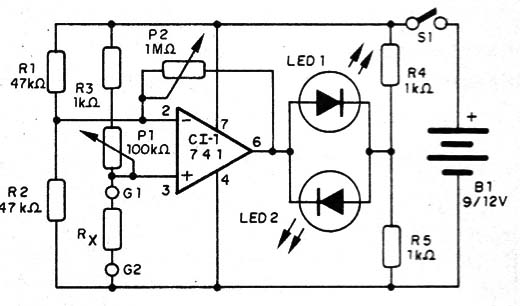
A alimentação pode ser feita por uma bateria de 9 V ou 12 V. Pode ser usada fonte.
Na figura 17 temos a placa de circuito impresso para a montagem.
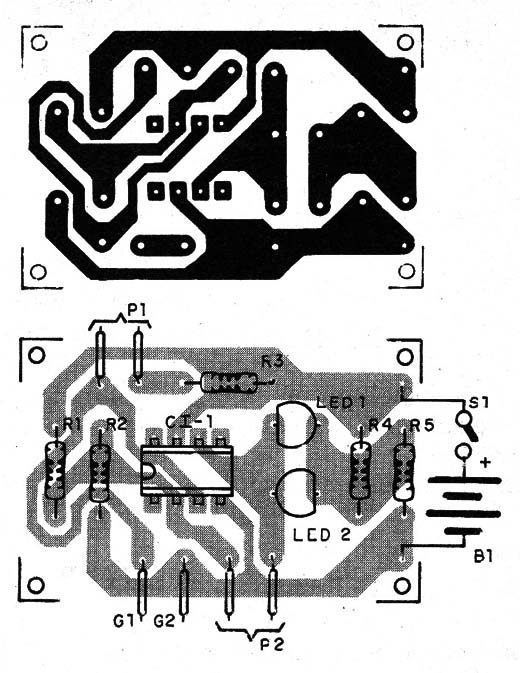
CI-1 – 741 – amplificador operacional
LED1, LED2 – LEDs vermelhos comuns
B1 - 9 V ou 12 V – bateria ou fonte
P1 – 100k – potenciômetro
P2 – 1 M – potenciômetro
S1 – Interruptor simples
R1, R2 – 47 k Ω x 1/8 W – resistores – amarelo, violeta, laranja
R3, R4, R5 – 1 k Ω x 1/8 W – resistores – amarelo, violeta, vermelho
G1, G2 – garras jacaré
Diversos:
Placa de circuito impresso, fios, conector para bateria ou fonte, caixa para montagem, solda, etc.
Conclusão
A ponte d Wheatstone consiste num recurso importante na medida de resistores muito pequenos ou muito grandes de resistências, quando instrumentos comuns podem falhar.
Em nosso artigo “Conheça as Pontes” (INS065), analisamos outros tipos de pontes de grande importância para a medida das mais diversas grandezas elétricas.



















