6.1 - Os Flip-Flops
O termo flip-flop, báscula ou multivibrador biestável é associado a um tipo de circuito que, apresentando apenas dois estados possíveis, se torna compatível com algumas aplicações de sequenciamento digital.
Por esse motivo, os flip-flops consistem em dispositivos de grande importância na implementação de projetos de eletrônica digital, merecendo uma lição completa à parte.
Esses circuitos podem ser usados para armazenar bits de informação, para fazer o sequenciamento de informações digitais e para fazer a divisão de freqüência de sinais digitais, além de muitas outras funções que ficarão claras a partir desse momento, no decorrer desse curso.
Analisemos então como funcionam os flip-flops ou multivibradores biestáveis.
Os flip-flops são elementos de circuito que podem apresentar em seu funcionamento apenas dois estados estáveis. Não existem estados intermediários entre estes dois estados.
Podemos compará-los a uma gangorra em que existem apenas dois estados estáveis possíveis: quando o lado A está no nível baixo ou lado B está no alto e quando o lado A está no alto o lado B está no baixo. As situações intermediárias são instáveis e não se mantém senão durante as transições ou mudanças de estado, conforme mostra a figura 140.
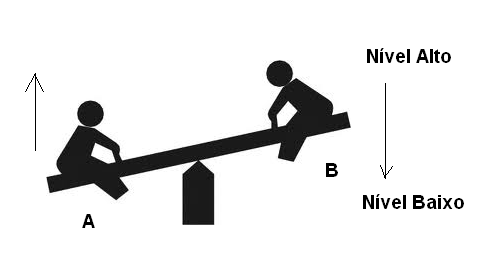
No caso específico de um flip-flop eletrônico, implementado com componentes como transistores, a aplicação de um sinal de entrada pode causar uma mudança de um estado para outro, e como a qualquer momento podemos saber qual é o estado em que ele se encontra, podemos considerar este circuito como uma unidade de memória capaz de armazenar um bit.;
Por essa capacidade de armazenamento, o flip-flop é usado como elemento básico de diversos tipos de memórias.
Existem diversos tipos de flip-flops que podem ser encontrados nos circuitos digitais.
Posteriormente, foram implementados flip-flops com transistores discretos e o passo final na sua evolução, foi a sua integração como elementos de circuitos integrados de famílias lógicas como a TTL, CMOS ou ainda em memórias de diversos tipos.
Para nós, em especial, interessa conhecer os tipos principais de flip-flops que podem ser encontrados nos circuitos integrados das famílias digitais principais, ou seja, TTL e CMOS e que analisaremos a partir de agora.
6.2 – Flip-flop R-S
O flip-flop R-S (de Reset e Set) – Este circuito tem sua configuração com transistores mostrada na figura 141, funcionando da seguinte maneira:
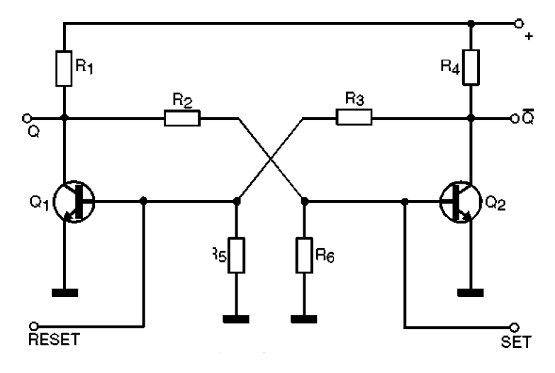
Quando alimentamos o circuito, dadas as mínimas diferenças que podem existir entre as características dos dois transistores, um deles conduzirá mais do que o outro. Supondo que este transistor seja Q1 o que ocorre é que há uma queda de tensão no seu coletor que reduz, em consequência, a corrente que polariza a base de Q2 via R2.
Nestas condições, a tensão do coletor de Q2 se mantém alta, realimentando a base de Q1 via R3 e a situação final do circuito é estabelecida: Q1 satura e Q2 fica no corte. O flip-flop encontra seu estado estável inicial.
O flip-flop R-S tem duas saídas, representadas por Q e /Q, assim na condição inicial estável com Q1 conduzindo Q estará no nível baixo (0) e /Q estará no nível alto (1).
O processo que leva o flip-flop a este estado inicial, pronto para funcionar é muito rápido, não demorando mais do que alguns microssegundos, ou mesmo nanossegundos dependendo dos componentes usados.
Quando o flip-flop se encontra na situação indicada, com Q=0 e /Q=1 dizemos que ele se encontra "setado" ou ainda fixado (o termo "armado" também pode ser usado).
A mudança de estado do flip-flop pode ser obtida aplicando-se um sinal na entrada conveniente. Como usamos transistores NPN, para comutar o flip-flop, temos de fazer conduzir por um instante o transistor que está cortado, ou seja, devemos aplicar um pulso positivo na entrada correspondente.
Assim, estando o flip-flop na condição indicada e desejarmos mudar o estado, aplicamos o pulso na entrada SET. O transistor Q2 conduz por um instante, realimentando via R3 a base de Q1 que é cortado. Com o corte, a tensão na base de Q2 sobe via polarização de R2, e mesmo que o pulso de disparo desapareça, o circuito se mantém no novo estado graças à realimentação.
Sua saída Q vai ao nível (1) e a saída /Q vai ao nível (0).
Para trocar novamente de estado o flip-flop R-S, aplicamos um pulso positivo na entrada RESET levando Q1 a saturação e Q2 ao corte, situação que se firma mesmo depois de desaparecido o pulso graças à realimentação proporcionada pelos resistores.
Veja que um pulso aplicado à entrada SET, o que corresponde a um bit 1, faz com que a saída Q que estava em 0 passe a 1 armazenando este bit. O flip-flop funciona realmente como uma memória para este bit.
Da mesma forma como utilizamos transistores bipolares NPN para obter um flip-flop, podemos também empregar outros tipos de componentes em configurações semelhantes. Podemos, por exemplo, elaborar flip-flops usando transistores PNP caso em que a polaridade dos sinais de disparo vai ser invertida.
Da mesma forma, podemos usar transistores de efeito de campo (FET), tanto de canal N como canal P (bipolares ou JFETs) como também transistores de efeito de campo MOS, com os dois tipos de canal (N ou P). O que vai mudar em cada caso é o sentido de circulação das correntes e as polaridades dos sinais aplicados.
Conforme já falamos, e veremos em detalhes no último item desta lição, os flip-flops também podem ser feitos com válvulas e na realidade os primeiros que existiram eram justamente montados com estes componentes. Naquela época não existiam transistores (bipolares ou FETs) e nem circuitos integrados.
Os flip-flops podem ser elaborados com portas lógicas e o R-S que estudamos pode ser facilmente obtido a partir de duas portas NAND de duas entradas, conforme mostra a figura 142.
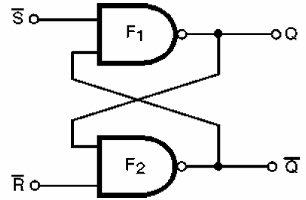
Levando em conta as tabelas verdade das portas NAND, vemos que a saída da primeira porta realimenta a segunda e vice-versa, garantindo assim a manutenção dos estados obtidos quando o flip-flop comuta.
No entanto, a comutação deste circuito ocorre quando as entradas passam do nível alto para o baixo, ou seja, de 1 para 0. Esta condição é indicada pelos símbolos /R e /S nas entradas.
O leitor pode então perceber que, quando as entradas estão ambas no nível baixo, o flip-flop se mantém no estado em que foi colocado por ser ligado ou por uma comutação anterior.
Por outro lado, se as entradas forem levadas simultaneamente ao nível alto, o flip-flop vai para um estado indeterminado que deve ser evitado. Na prática, a aplicação de níveis altos (1) nas duas entradas pode destruir o dispositivo.
O diagrama de tempos da figura 143 mostra o que ocorre no funcionamento de um flip-flop por etapas que podem ser analisadas da seguinte forma.
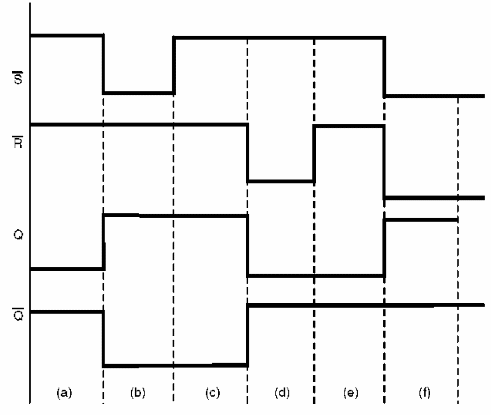
Na figura temos as seguintes condições do flip-flop a serem consideradas:
a) Flip-flop ressetado
b) /S vai ao nível baixo e o flip-flop é setado
c) /S vai ao nível alto e o flip-flop permanece setado
d) /R vai ao nível baixo e o flip-flop é ressetado
e) /R volta ao nível alto e o flip-flop permanece ressetado
Tudo isso pode ser representado por uma tabela verdade, da mesma forma que fazemos com as funções lógicas. Nesta tabela temos alguns novos símbolos com os quais o leitor deve começar a se familiarizar e que são amplamente usados em eletrônica digital, a saber:
a) Primeira possibilidade
Qn-1 = representa o estado da saída Q ANTES da aplicação dos sinais.
Qn = representa o estado da saída Q DEPOIS da aplicação dos sinais.
b) Segunda possibilidade
Q = representa o estado da saída Q ANTES da aplicação dos sinais.
Qn+1 = representa o estado da saída Q DEPOIS da aplicação dos sinais.
Obs: em lugar de n em alguns livros encontramos a letra t.
Os dois tipos de representação são usados.
Nas colunas e linhas em que são colocados os níveis lógicos 0 e 1, quando aparece o termo Qn ou /Qn isso indica que a saída vai para um estado indeterminado.
A tabela verdade do flip-flop R-S com portas NAND fica então:
| R | S | Qn+1 | /Qn+1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | Qn | /Qn |
Para obtermos um flip-flop R-S também podemos usar portas NOR, conforme mostra a figura 144.

Na figura 145 temos os símbolos adotados para representar este tipo de flip-flop.
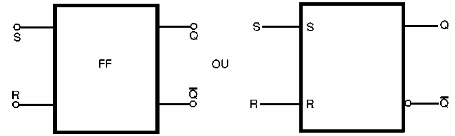
Este circuito também é chamado de R-S NOR LATCH, da mesma forma que o circuito anterior é denominado R-S NAND LATCH.
A palavra "latch" significa trava, o que nos sugere que se trata de um circuito que "trava" numa certa posição a partir dos comandos R e S e que usa portas NAND ou NOR. O termo latch, em inglês pode, portanto, também ser associado a flip-flops.
6.2.1 – Repiques
Quando fechamos um interruptor, ou ainda um sensor é acionado, o estabelecimento da corrente no circuito não é imediato. Os contatos mecânicos tendem a oscilar, causando assim pulsos de variação da tensão ou da corrente, denominados repiques, ou usando o termo inglês “bounce” (balanço),
Esses repiques fazem com que o circuito digital que deva receber o comando do interruptor ou sensor interprete o sinal de entrada como mais de um pulso, conforme mostra a figura 146.

Neste caso, o fechamento do sensor é interpretado como uma sequência de três pulsos. Se o circuito tiver de contar pulsos, a contagem será de 3, e não apenas um fechamento.
6.3 – Flip-flops RS com Clock Mestre-Escravo
Este circuito, chamado de flip-flop R-S controlado por clock (*) e mestre escravo, encontra uma gama de aplicações muito grande nos circuitos digitais mais complexos, já que eles são sempre comandados por um clock, ou seja, são circuitos lógicos sincronizados.
O uso de um circuito de controle (mestre) que determina quando o flip-flop (escravo) muda de estado é importante para permitir que as mudanças de estado do flip-flop só ocorram em instantes bem determinados.
Usando portas NAND podemos inicialmente implementar um flip-flop R-S controlado por clock (Master-Slave) conforme mostra a figura 147.
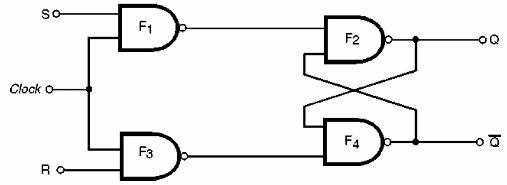
Analisemos seu funcionamento:
Partindo da situação em que a entrada de clock (relógio) esteja no nível baixo, as saídas Q e /Q permanecerão no estado inicial em que se encontravam e insensíveis a qualquer variação que ocorra nas entradas S e R (set e reset).
Quando a entrada de clock for levada ao nível 1, o circuito passa a responder aos sinais das entradas R e S.
No entanto, conforme mostra o diagrama de tempos da figura 148, este circuito tem um inconveniente.
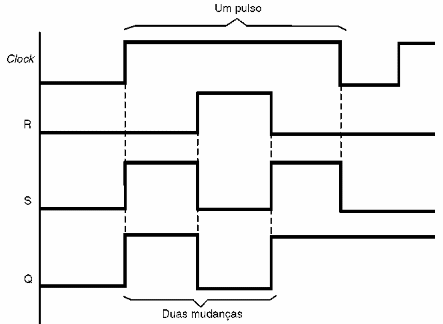
Como as saídas acompanham as entradas, durante o tempo em que o clock as habilita, estas saídas podem mudar de estado mais de uma vez, voltando assim ao estado inicial, o que não é desejado de forma alguma, pois levaria o circuito a uma instabilidade de funcionamento.
Um modo de contornar este problema consiste na utilização de duas etapas numa configuração mais complexa, que é mostrada na figura 149.
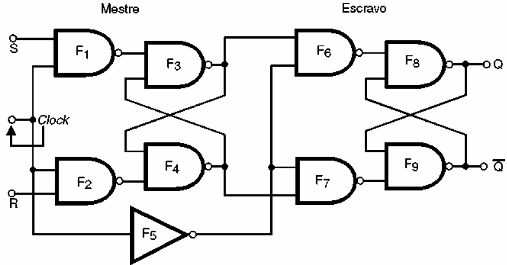
Obtém-se então uma configuração mais elaborada em que se isola a etapa de saída que o flip-flop propriamente dito e a etapa de controle, em que temos os comandos set e reset.
Este circuito é denominado Flip-Flop R-S Mestre-Escravo ou Flip-Flop R-S Master-Slave podendo fazer uso, tanto de portas NAND, como um inversor cuja finalidade é inverter o pulso de clock (F5).
Isolando as duas etapas, as mudanças de sinal que ocorrem na primeira etapa não afetam a segunda etapa, a não ser quando isso é necessário.
O que ocorre neste caso é que, quando a entrada de clock for ao nível 1, o flip-flop mestre mudará de estado, mas o flip-flop escravo permanecerá insensível, mantendo seu estado.
Quando a entrada de clock passar para o nível lógico 0, a saída do flip-flop mestre será levada para o escravo.
Isso significa que o flip-flop, em seu todo, não é sensível ao nível do sinal de clock, ou seja, se ele é 0 ou 1, mas sim à sua transição. As saídas Q e /Q só vão mudar de estado no instante em que ocorrer a transição, do sinal de clock do nível alto para o nível baixo.
Com esta configuração é possível garantir que só vai ocorrer uma mudança de estado na presença de um pulso de clock.
Os flip-flops que funcionam desta forma são denominados "Edge Triggered" ou "Disparados pela Borda", referindo-se ao pulso de disparo.
O termo "borda" se refere a transição de um sinal, ou seja, ao trecho da curva que representa a tensão em que ela varia entre o nível 0 e 1 (borda de subida), ou do nível 1 ao 0 (borda de descida). Também é comum usar o termo "fronte" para indicar estas variações.
Assim, também chamamos "fronte positiva" ao trecho em que ocorre a variação do sinal de 0 a 1 e fonte negativa ao trecho que temos a variação de 1 a 0.
Se a mudança de estado ou disparo (gatilhamento) ocorre quando o sinal de clock passa de 0 para 1, os flip-flops são denominados "positive edge-triggered" (disparados pela borda ou fronte positiva), enquanto que, se o disparo ocorre quando o clock vai do nível 1 para 0, ou seja, na queda do nível lógico, os flip-flops são chamados de "negative edge-triggered" (disparados pela borda ou fronte negativa).
A maioria dos flip-flops deste tipo disponíveis na forma de circuito integrado é do tipo acionado pela transição negativa do sinal de clock.
Na figura 150 temos uma representação mais comum para este tipo de flip-flop, em que temos os circuitos internos, para o caso do sinal de clock ser aplicado diretamente ao flip-flop mestre (M).

No entanto,m na simbologia mais usual, temos a representação mostrada na figura 151 em que se leva em conta apenas as entradas e saídas.
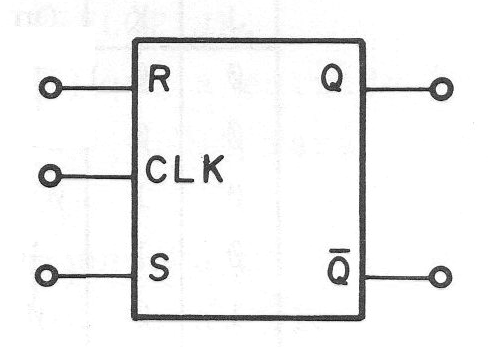
Quando este tipo de flip-flop é usado num projeto de maior velocidade, é muito importante levar em conta os tempos em que todo o processo ocorre.
Assim, partindo do diagrama de tempos da figura 152, vemos que a saída do flip-flop só completa sua mudança de estado depois de certo tempo, a partir do instante em que o pulso de clock foi aplicado.
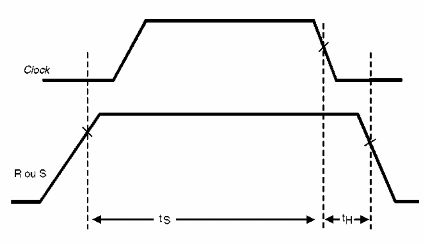
Dois tempos são importantes neste tipo de circuito.
a) th é chamado de Hold Time ou Tempo de Manutenção e é o tempo em que a entrada deve permanecer ainda no circuito para que seu nível lógico seja reconhecido pelo flip-flop.
b) ts é chamado de Setup Time ou tempo de fixação e é o tempo em que a entrada do flip-flop deve permanecer no estado desejado, antes da transição do clock que vai provocar a mudança de estado do circuito.
Duas entradas podem ser acrescentadas neste circuito, conforme mostra a figura 153, dotando-o de recursos importantes para aplicações práticas.
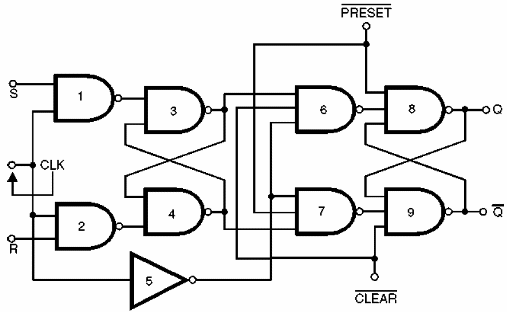
Uma das entradas é denominada PRESET (/PR), ou pré-ajuste, e tem por função levar imediatamente as saídas do circuito a um estado determinado (Q=1 e /Q=0) independentemente do que pode estar acontecendo nas demais entradas.
Sua ativação ocorre quando /PR estiver em 0 e /CLR em 1, no caso indicado, pois a / sobre a identificação indica que ela está ativa no nível baixo.
A outra entrada denominada CLEAR, ou apagamento, tem por função levar as saídas aos estados Q=0 e /Q=1 independentemente do que estiver ocorrendo nas demais entradas.
Na figura 154 temos a representação comum para este tipo de flip-flop.
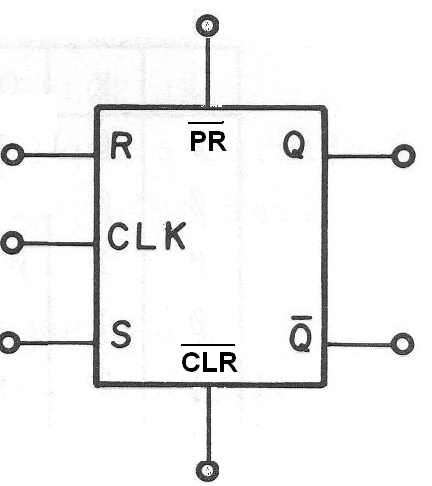
É importante observar que estas duas entradas não podem ser ativadas ao mesmo tempo, pois isso levaria o circuito a um estado indeterminado que inclusive pode causar problemas aos seus componentes.
Já alertamos que é comum que em funções mais complexas, como os flip-flops, existam "situações proibidas". Existem combinações de níveis lógicos que não podem estar presentes ao mesmo tempo em determinadas entradas, pois podem levar o circuito a um estado indefinido, ou seja, em que não é possível prever, o que vai ocorrer com a saída. Um exemplo simples é o de aplicarmos ao mesmo tempos níveis de disparo nas entradas Set e Reset de um flip-flop ao mesmo tempo.
Voltando ao nosso exemplo, a tabela verdade para esse circuito nos mostra três novos símbolos que normalmente são usados em eletrônica digital.
X representa uma condição irrelevante, ou seja, qualquer que ela seja não haverá influência no que ocorre na saída.
A seta para cima indica a transição do nível baixo para o nível do sinal na entrada ou saída representadas enquanto que a seta apontando para baixo indica uma transição do nível alto para o nível alto do sinal correspondente.
|
/CLR |
/PR |
R |
S |
CLK |
Qn+1 |
/Qn+1 |
|
0 |
0 |
x |
x |
x |
1 |
1 |
|
0 |
1 |
x |
x |
x |
0 |
1 |
|
1 |
0 |
x |
x |
x |
1 |
0 |
|
1 |
1 |
0 |
0 |
↓ |
Qn |
/Qn |
|
1 |
1 |
0 |
1 |
↓ |
1 |
0 |
|
1 |
1 |
1 |
0 |
↓ |
0 |
1 |
|
1 |
1 |
1 |
1 |
↓ |
1 |
1 |
X- não importa
Qn e /Qn – não muda
6.4 - O flip-flop J-K Mestre-Escravo
Mesmo usando duas etapas, o flip-flop que vimos ainda pode apresentar alguns problemas de funcionamento quando usado em determinadas aplicações. Um aperfeiçoamento desse circuito é que veremos a seguir.
O flip-flop J-K mestre-escravo ou "master-slave", como as demais funções que estudamos, pode ser implementado por funções lógicas comuns adquirindo a configuração básica mostrada na figura 155.
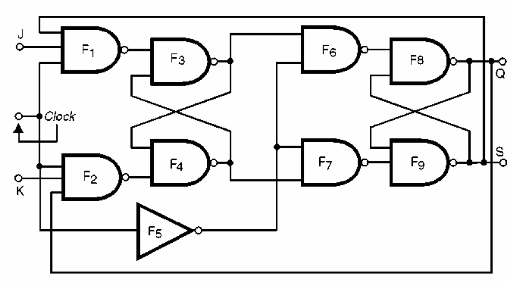
Um problema que observamos nos flip-flops R-S é que temos uma situação "proibida" que ocorre quando as entradas R e S vão ao nível alto ao mesmo tempo, o que pode levar o circuito a um estado indeterminado, conforme já alertamos.
Essa situação ocorre principalmente nas aplicações em computação e controle quando uma parte do sinal de saída é usada para realimentar a entrada. Nestas condições podem ocorrer as situações de conflito, com a produção de oscilações indesejadas e mesmo resultados imprevisíveis nos circuitos que devem ser excitados.
Essa situação pode ser contornada com a utilização de uma nova configuração que é justamente a do flip-flop J-K, e que analisaremos a seguir. Essa configuração, por suas vantagens em determinados circuitos é a mais utilizada nas aplicações práticas.
Partimos então das entradas desse tipo de flip-flop. Podemos ter quatro combinações possíveis para os sinais aplicados nas entradas J e K, conforme mostra a tabela abaixo.
J K
0 0
1 0
0 1
1 1
Analisemos cada uma delas:
a) J = 0 e K = 0
Quando a entrada de clock (CLK) passa por uma transição negativa, do sinal o flip-flop mantém sua condição original não mudando de estado.
b) J = 1 e K = 0
Quando a entrada de clock (CLK) passa por uma transição negativa, o flip-flop é "setado". Se já estiver setado ele permanece nesta condição.
c) J = 0 e K = 1
Quando a entrada de clock (CLK) passa por uma transição negativa, o flip-flop é "ressetado". Se já estiver nesta condição ele permanece.
d) J = 1 e K = 1
Nessa condição, ao receber uma transição negativa na entrada de clock (CLK), o flip-flop muda de estado (TOGGLE) (*). Se estiver setado ele resseta e se estiver ressetado ele é setado.
Podemos elaborar a tabela verdade da figura 156 para indicar o que ocorre com este flip-flop.
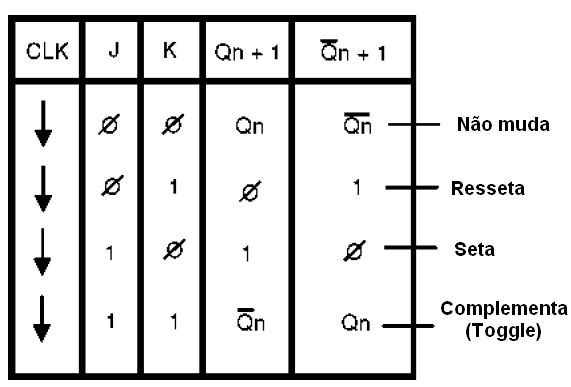
Observe o uso das setas para indicar as transições de sinal na entrada de clock, as quais comandam o funcionamento desse tipo de circuito.
Da mesma forma que nas outras configurações que estudamos, podemos também incluir as entradas de PRESET e CLEAR neste circuito, que ficará da maneira mostrada na figura 157.
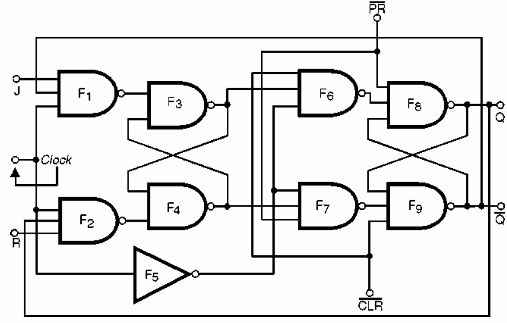
Uma tabela verdade incluindo as entradas de PRESET (PR) e CLEAR (CLR) é mostrada abaixo.
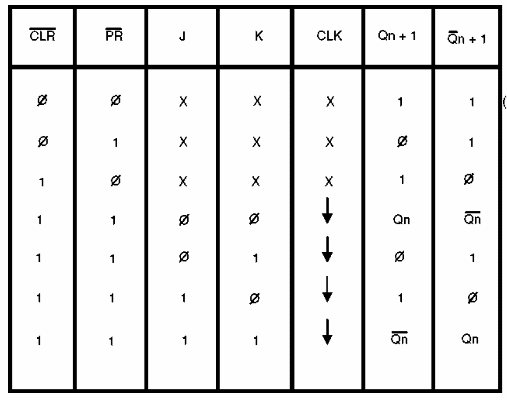
Uma maneira melhor de analisarmos o funcionamento deste circuito é através de um diagrama de tempos, em que observamos as formas de onda nos diversos pontos de entrada e saída. Este diagrama de tempos para o flip-flop J-K é mostrado na figura 158.
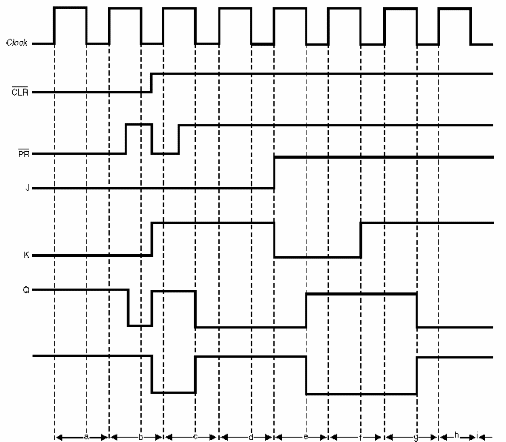
Analisemos alguns trechos importantes deste diagrama. mostrando o que acontece:
a) Nesse instante, CLR e PR estão no nível baixo, Q e /Q estão no nível alto, que é uma condição não permitida.
b) Aplica-se então o sinal PR que, indo ao nivel alto, faz com que o flip-flop seja ressetado.
c) A aplicação de um pulso na entrada CLR que vai ao nível alto, e a ida de PR ao nível baixo, faz agora com que o flip-flop seja setado.
d) CLR e PR são mantidos no nível alto a partir deste instante. Com J = 0 neste trecho e K indo ao nível alto, o flip-flop será ressetado na próxima transição negativa do sinal de clock.
e) Ainda com CLR e PR no nível alto (esta condição se manterá daqui por diante), e a saída J = 0 e k = 1, o flip-flop permanece ressetado.
f) Com J = 1 e K = 0, o flip-flop é setado na transição seguinte do pulso de clock.
g) Com J = 1 e K = 0 não ocorrem mudanças de estado.
h) Com J = 1 e K = 1 na transição seguinte do pulso de clock o flip-flop muda de estado (complementa ou "toggle"). Se estiver ressetado, como neste caso, ele é setado.
i) Mantendo j = 1 e K = 1 com nova transição do pulso de clock, o flip-flop muda de estado outra vez, ou seja, complementa.
Veja que quando as entradas J e K estão no nível alto, o circuito se comporta como um disparador, mudando de estado a cada transição negativa do pulso de clock.
Conforme o leitor verá nas lições futuras, na maioria das aplicações digitais, o funcionamento é dinâmico, com os níveis de entrada e saídas das diversas funções mudando constantemente. Isso significa que, em muitas aplicações, a análise do circuito não se limita saber o que ocorre com uma saída quando determinadas entradas apresentam determinados níveis.
Pode ser necessário analisar a dinâmica do funcionamento do circuito e, nesse caso, os diagramas de tempo são muito mais apropriados.
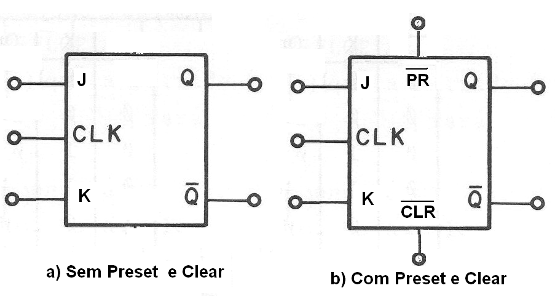
O símbolo usual para este tipo de flip-flop é o mostrado na figura 159.
6.5 - O flip-flop tipo D
Os flip-flops tipo D também encontram uma vasta gama de aplicações práticas. Na figura 160 temos o símbolo adotado para representar esse tipo de flip-flop.
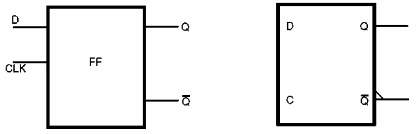
O flip-flop tipo D possui uma única entrada que comanda todo o seu funcionamento. Esta entrada é que lhe dá nome. Denominada "Data" (dados), ela é abreviada por D e daí o nome do dispositivo.
Esse flip-flop opera de uma maneira muito simples: no pulso de clock ele assume o estado da entrada, conforme podemos ver pela sua tabela verdade:
D Qn+1
0 0
1 1
Pela sua simplicidade de funcionamento ele funciona muito bem aplicações como divisores de frequência, contadores de pulsos, etc.
6.6 – Flip-flop tipo T
O nome deste flip-flop vem de "Toggle" (T) ou complementação, e seu símbolo é mostrado na figura 161.
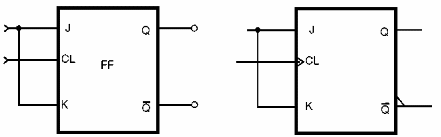
O que esse circuito faz pode ser entendido facilmente pelo diagrama de tempos mostrado na figura 162.
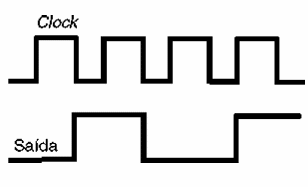
Quando a entrada T desse circuito está no nível baixo, o flip-flop se mantém em seu estado anterior, mesmo com a aplicação do pulso de clock. No entanto, quando a entrada T está no nível alto, o flip-flop muda de estado. Se estava setado ele resseta, e se estava ressetado, ele seta.
Este comportamento significa na realidade a divisão da frequência do clock por dois. Em outras palavras, esse circuito se comporta como um divisor de frequência, encontrando aplicações práticas bastante importantes em eletrônica digital.
Um exemplo de aplicação é dado na figura 163 em que associamos diversos flip-flops do tipo T em série de modo que, passando por cada um a frequência do sinal de entrada, temos a sua divisão por 2.

Usando 4 flip-flops, podemos dividir a frequência de um sinal de entrada por valores que sejam potências de 2, como: 2, 4, 8 e 16.
Esse tipo de divisor de frequência é muito usado, a ponto de existirem circuitos integrados que possuem sequências de mais de 10 flip-flops ligados desta forma.
Na prática não temos os flip-flops tipo T como componentes prontos para uso. O que se pode fazer é obter este flip-flop a partir de outros e isso será visto no item seguinte.
6.7 – Transformando Flip-Flops
Da mesma maneira como podemos obter qualquer função lógica complexa a partir de funções simples, o que foi visto em lições anteriores, também podemos "brincar" com os flip-flops, obtendo outros tipos a partir de um tipo básico.
Assim, usando um flip-flops R-S ou J-K, que são comuns, e algumas portas lógicas, podemos obter flip-flops de outros tipos.
Na figura 164 temos algumas conversões que podem ser feitas utilizando-se flip-flops do tipo R-S.

O modo de funcionamento de cada um pode ser facilmente entendido se o leitor tentar associar as tabelas verdades dos flip-flops que foram estudados nesta lição às tabelas verdade das portas agregadas, considerando os sinais de realimentação.
Assim, começamos pela figura 165, onde temos o modo de se obter flip-flops tipo D e T a partir de flip-flops do tipo J-K.
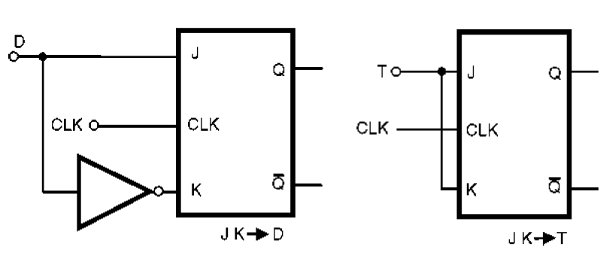
Veja que a simples conexão da entrada K ao J no flip-flop do tipo J-K o transforma em um flip-flop tipo T. Esta possibilidade é muito interessante, já que flip-flops J-K são disponíveis em tecnologia tanto TTL como CMOS e podem ser usados em circuitos divisores de frequência.
Quando falarmos dos tipos específicos de circuitos integrados de flip-flops das famílias TTL e CMOS, o leitor terá informações sobre diversos tipos de flip-flops que podem ser usados em projetos práticos.
Na verdade, já utilizamos esta configuração em diversos de nossos projetos práticos publicados em livros, revistas e no nosso site.
Finalmente temos outras duas transformações importantes de flip-flops que são mostradas na figura 166.

No primeiro caso temos uma transformação de um flip-flop tipo D em flip-flop tipo T, bastando para isso que a saída complementar /Q seja ligada à entrada D, realimentando o circuito.
A segunda transformação, que leva um flip-flop tipo D a funcionar como tipo T, exige o emprego de uma porta AND adicional na realimentação do sinal que é retirado da saída complementar /Q.
Veja que é muito importante saber transformar flip-flops, assim como as funções lógicas. Muitos circuitos integrados possuem mais de um flip-flop disponível no mesmo invólucro. Assim, se precisarmos de um flip-flop do tipo D e de um tipo T, podemos usar um circuito que tenha dois do tipo D e transformar um deles e um do tipo T.
O resultado é que, com um componente apenas, obtemos as duas funções, com economia de custo e espaço na placa de circuito impresso.
6.8 – Nos equipamentos digitais
Encontramos os flip-flops nos computadores, equipamentos de telecomunicações, controles industriais, equipamentos de eletrônica embarcada, robôs e muitos outros, como elementos fundamentais de muitos circuitos.
Uma das aplicações mais importantes do flip-flop é na divisão de frequência de clocks. Conforme o leitor sabe, existem setores de um equipamento digital que devem operar com velocidades menores que a fornecida pelo clock principal.
É o caso dos barramentos de microcontroladores e microprocessadores e controles diversos onde são ligadas as placas de expansão, aquisição de dados e controle, modems, as saídas de dados das portas paralela e serial, etc.
Assim, em lugar de se usar um clock para cada frequência desejada, o que se faz ‚ empregar um clock único e dividir sua frequência conforme as exigências de frequências mais baixas, conforme mostra a figura 167.
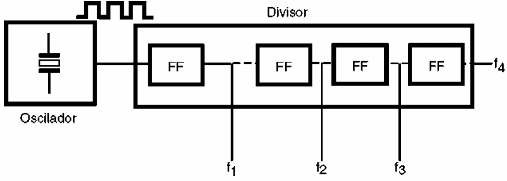
No caso de muitos equipamentos digitais, tanto o próprio clock como a sequência de flip-flops divisores pode ser obtida num único circuito integrado.
Um ponto importante que deve ser levado em conta, e que estudaremos nas lições futuras, é que podemos ligar os flip-flops em conjunto com outras funções, de modo que a frequência possa ser dividida por qualquer número, e não somente por potências de 2 como 2, 4, 8, 16, 32, 64, 128, etc. Como isso é feito, será estudado mais adiante.
Outra aplicação importante é como célula de memória. Oito flip-flops ligados lado a lado podem armazenar um byte inteiro. Cada flip-flop armazena um bit.
Existem diversas memórias internas, usadas em equipamentos digitais que nada mais do que flip-flops organizados em matrizes, contendo grande quantidade deles, e que podem ser habilitados tanto para a leitura de dados como para introdução (gravação de dados).
Existem ainda muitas outras funções importantes que podem ser implementadas a partir de flip-flops e que serão estudadas nas lições seguintes.
6.9. Os flip-flops antigos
A configuração do flip-flop não é nova. Na verdade foi em 1919 que dois pesquisadores americanos chamados Eccles e Jordan apresentaram o primeiro circuito de flip-flop usando válvulas, conforme mostra a figura 168.

Por este motivo, muitos profissionais "da velha guarda" ainda chamam os flip-flops de "Basculas ou Circuitos Eccles-Jordan" quando referem-se a esta configuração.
Em 1930 os físicos já usavam estes circuitos ligados em série para dividir a contagem dos pulsos de contadores Geiger de radiação de modo a obterem valores menores mais facilmente totalizados nas pesquisas.
Um contador binário usando uma lâmpada neon ligada às válvulas foi desenvolvido usando estes flip-flops já em 1940, mas, foi somente depois dessa época que os primeiros computadores digitais passaram a usar estes circuitos de uma forma mais intensa, até o advento do transistor e depois dos circuitos integrados.
Índice
Curso de Eletrônica Digital – Analógica e Digital – Sistemas de Numeração (CUR5001)
Curso de Eletrônica Digital – A Álgebra de Boole (CUR5002)
Curso de Eletrônica Digital – Famílias de Circuitos Lógicos Digitais (CUR5003)
Curso de Eletrônica - Eletrônica Digital – A Família de Circuitos Integrados CMOS (CUR5004)
Curso de Eletrônica Digital – Combinando Funções Lógicas - (Lógica Combinacional) (CUR5005)
Curso de Eletrônica - Eletrônica Digital - Os Elementos Biestáveis (CUR5006)
Curso de Eletrônica - Eletrônica Digital - Flip-Flops e Funções Integradas em CIs (CUR5007)
Curso de Eletrônica - Eletrônica Digital - Os Multivibradores Astáveis e Monoestáveis (CUR5008)
Curso de Eletrônica - Eletrônica Digital - Os Contadores Digitais (CUR5009)
Curso de Eletrônica - Eletrônica Digital - Memórias, ADCs e DACs (CUR5013)



















