
De todos os componentes eletrônicos, os capacitores eletrolíticos pouco evoluíram em relação ao princípio básico de funcionamento. Apesar de melhorias no que se refere as características mais críticas, eles ainda operam segundo os mesmos princípios eletroquímicos originais o que os torna particularmente sensíveis em qualquer projeto. Vejas neste artigo algumas das principais características dos capacitores eletrolíticos para que elas possam ser levadas em conta nos projetos mais críticos.
Capacitores são componentes que armazenam cargas elétricas.
Formados por dois condutores entre os quais é colocado um dielétrico, eles são especificados em Farads (F) e seus submúltiplos (microfarad, nanofarad e picofarad).
A figura 1 mostra a estrutura básica de um capacitor.
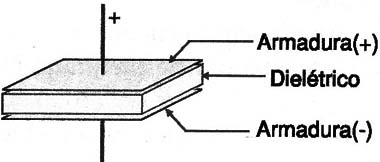
A quantidade de cargas que um capacitor pode armazenar é dada pela conhecida fórmula:
Q = C x.V
Onde:
Q é a quantidade de cargas (coulombs)
C é a capacitância (farads)
V é a tensão entre as armaduras (V)
A quantidade de energia armazenada, por outro lado é dada por:
P = ½ x C x V2
Onde:
P é a energia armazenada em joules
C é a capacitância em farads
V é a tensão em volts
Os Capacitores Eletrolíticos
Os capacitores eletrolíticos se diferenciam dos demais pela espessura extremamente pequena do seu dielétrico, conforme mostra a figura 2.
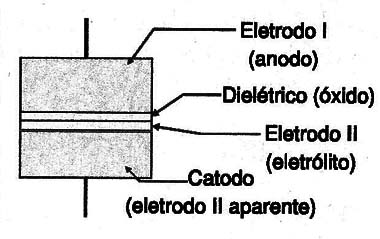
Nos tipos comuns são os usados os mesmos materiais para os eletrodos I e II .
Esse material pode ser o alumínio (Al), tântalo (Ta), nióbio (Nb), titânio (Ti), zircônio Zr), háfnio (Hf) além de outros cujas características permitam.
Sobre esses eletrodos de metal durante um processo de oxidação anódica forma-se uma finíssima camada de óxido do metal usado a qual consiste num dielétrico.
Atualmente, os capacitores mais usados são os que fazem uso do alumínio e o tântalo.
Como a constante dielétrica do óxido de tântalo é maior do que a do óxido de alumínio, os capacitores de tântalo, para uma mesma capacitância podem ser bem menores, conforme mostra a figura 3.,
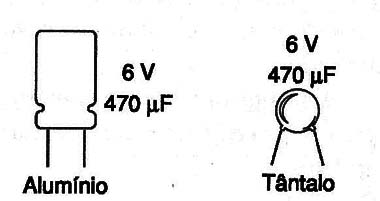
Como o óxido necessita de um processo que envolve uma polarização, os capacitores eletrolíticos são componentes polarizados.
Na figura 4 temos a estrutura bastante aumentada de um capacitor de modo que o leitor perceba que a camada de dielétrico não é perfeitamente regular.
Um capacitor real não representa apenas um capacitância para um circuito externo.
Na verdade ele possui elementos parasitas que se devem a resistência dos terminais, indutância do próprio material condutor que é enrolado, etc.
Assim, o circuito equivalente a um capacitor eletrolítico é o mostrado na figura 5.
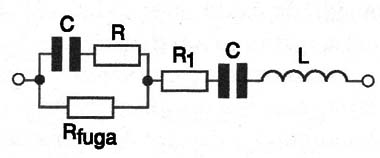
A indutância em série é especialmente importante quando usamos os capacitores em circuitos de altas freqüências.
Por exemplo, essa indutância impede que esses componentes sejam usados de forma eficiente no desacoplamento de sinais de altas freqüências.
Construção
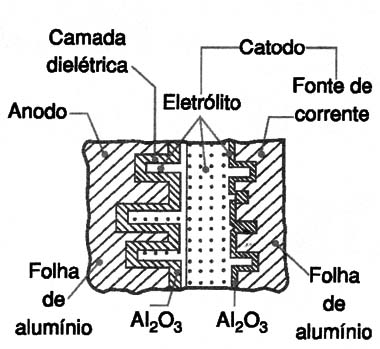
A figura 6 mostra uma vista em corte de um capacitor eletrolítico típico, para que o leito tenha uma idéia de como esse componente é fabricado.
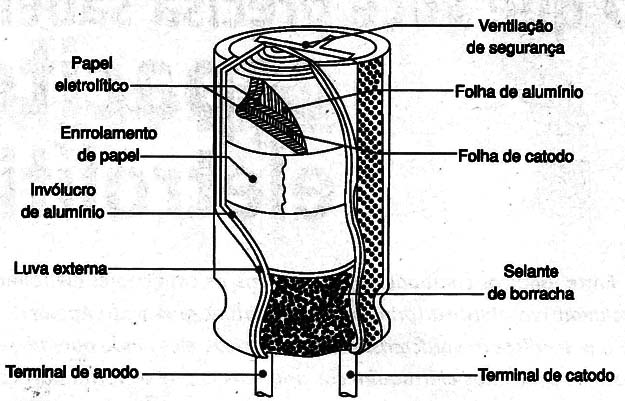
Nessa figura temos a construção típica de um capacitor com terminais paralelos.
Especificações
A partir dessas informações iniciais, podemos passar às especificações dos capacitores eletrolíticos e o que elas significam.
a) Capacitância nominal
É a capacitância indicada no componente, ou seja, seu valor em Farads (submúltiplos).
b) Corrente de Fuga
Quando uma tensão DC é aplicada ao capacitor uma pequena corrente flui devido ao fato do dielétrico não ser um isolante perfeito e outros fatores, como umidade, características do invólucro, etc.
c) Tangente do Ângulo de Perda e Fator de Dissipação
Como um capacitor real não representa uma capacitância pura, mas possui uma resistência equivalente em série (ESR), operando em corrente alternada, temos uma defasagem corrente tensão, conforme o gráfico mostrado na figura 7, a qual é responsável por uma dissipação de potência.
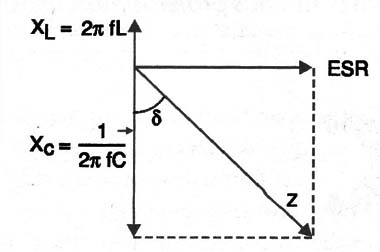
A tangente do ângulo de perda (tg δ) é dada pela relação entre a ESR e a reatância capacitiva, Xc conforme a seguinte fórmula:
tg δ = ESR/Xc
O fator de dissipação, por outro lado pode ser calculado em função da ESR para se obter as perdas na sua resistência ohmica.
ESR = Tg δ / 2. δ x f x C
Onde:
f é a freqüência em Hz
C é a capacitância em farads
d) Faixa de Temperaturas de Operação
Trata-se de faixa de temperaturas ambiente para o qual o capacitor foi projetado para operar de modo contínuo.
e) Tensão de Trabalho
Trata-se da tensão DC máxima para a qual o capacitor foi projetado.
Essa tensão é dada pela soma da tensão DC com a tensão AC de pico aplicada ao capacitor.
f) Tolerância
Da mesma forma em que outros componentes, existe uma tolerância de valores que é a diferença máxima que pode haver entre o valor especificado e o valor encontrado de capacitância.
g) Tensão de Surto
Essa é uma aplicação importante quando o capacitor é usado em controles de potência e outros circuitos que estejam sujeitos a surtos de tensão.
Trata-se da tensão máxima DC que o capacitor pode ficar sujeito em temperaturas normais diretamente 30 segundos em intervalos não menores do que 5 minutos.
Normalmente ela se relaciona com a tensão nominal, conforme as seguintes tabelas:
| Tensão Nominal (V) | 4 | 6,3 | 10 | 16 | 25 | 35 | 40 |
| Tensão de surto (V) | 5 | 8 | 13 | 20 | 32 | 44 | 50 |
| Tensão Nominal (V) | 50 | 63 | 80 | 100 | 160 | 180 | 200 |
| Tensão de Surto (V) | 63 | 79 | 100 | 125 | 200 | 225 | 250 |
| Tensão Nominal (V) | 250 | 315 | 350 | 400 | 450 |
| Tensão de surto (V) | 300 | 365 | 400 | 450 | 500 |
h) Corrente de Ripple
Uma tensão corrente alternada ou pulsante superposta a uma tensão DC aplicada a um capacitor resulta numa corrente alternada circulando pelo capacitor.
Levando em conta as perdas pela resistência ohmica e no dielétrico, essa corrente provoca um aumento da temperatura do capacitor.
A quantidade de calor gerado nesse processo depende da forma de onda da corrente e de sua freqüência.
Os capacitores eletrolíticos devem ter a corrente máxima de ripple (Ir) especificada, o que ocorre normalmente em função da temperatura ambiente.
Fórmulas permitem calcular a elevação da temperatura com essa corrente, devendo ser usadas nos projetos mais críticos, principalmente os ue envolvem capacitores não sólidos.
A figura 8 mostra o modo de se calcular a corrente RMS de ripple em função de diversas formas de onda.
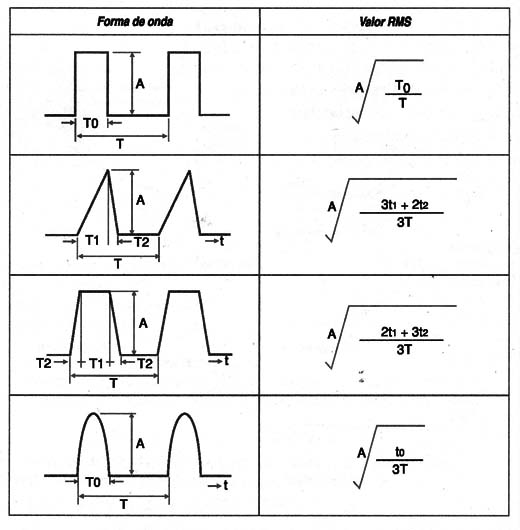
i) Impedância
A impedância de um capacitor eletrolítico depende de diversos fatores como a ESR e demais características do próprio componente e circuito de operação.
A ESR é normalmente especificada pelo fabricante do capacitor considerado.
j) Vida útil e Taxa de Falhas
A especificação da vida útil de um capacitor também é importante para a utilização de um capacitor eletrolítico.
A temperatura e a corrente de ripple são dois dos principais fatores que influem na vida útil de um capacitor eletrolítico. Para a temperatura é comum aplicar a regra do “reduz à metade a cada 10º C”.
Assim, para cada 10º C de aumento da temperatura a vida útil do capacitor reduz à metade em relação ao valor especificado pelo fabricante.
Essa regra, entretanto não é válida se o capacitor trabalhar com correntes de ripple intensas.
A taxa de falhas (?) é definida como o número de componentes que falham por unidade de tempo tomando o total de componentes de um certo lote observado.
Esse número é normalmente expresso pelo chamado “fit” (failures in time) sendo igual a 106 /horas dentro de um nível de confiabilidade (UCL) de 60%.
Esses valores são obtidos em testes de laboratório e também em observações de campo.
Uma curva interessante, denominada nos meios técnicos de “banheira” pelo seu formato, é a mostrada na figura 9.
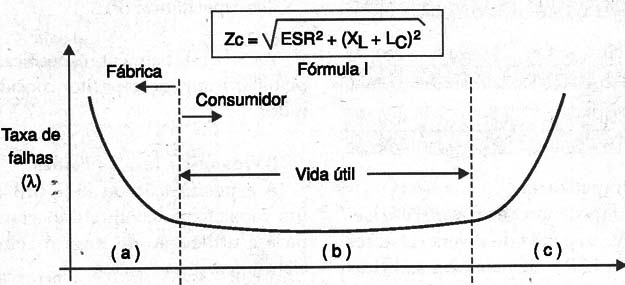
Essa curva nos mostra em (a) a existência de um período inicial de falhas que ocorre ainda durante o processo de fabricação. Trata-se do que se denomina “mortalidade infantil” dos capacitores eletrolíticos.
Depois em (b) temos a vida útil propriamente dita do capacitor, em que temos um número menor de falhas, seguinte uma média que é denominada porcentagem de falha.
Finalmente em (c) quando vence a vida útil, temos o aumento gradual ou deterioração do componente.
Características x Diversos Fatores
Conforme pudemos ver por esse artigo, as características dos capacitores eletrolíticos variam sob influência de diversos fatores externos.
O projetista que usa esses componentes deve estar atento para esse fato, principalmente se o produto final vai trabalhar sob condições ambientes que variam numa ampla faixa de valores, ou ainda em circuitos que estejam sujeitos a variações muito grandes.
Na figura 10 damos diversos gráficos que mostram como as diversas características de um capacitor eletrolítico variam com o tempo, freqüência, temperatura e tensão aplicada.



















