O projeto de filtros ativos usando amplificadores operacionais exige um certo conhecimento básico do princípio de funcionamento tanto de filtros passivos comuns como do próprio amplificador operacionais. Neste artigo explicamos alguns pontos importantes que envolvem o cálculo de filtros ativos usando amplificadores operacionais comuns (tanto bipolares como usando FETs) e que podem ser de grande utilidade para os leitores que trabalham com projetos envolvendo sinais analógicos.
Um filtro pode ser definido como um circuito capaz de se comportar de maneira seletiva diante de sinais analógicos de determinadas frequências. Os filtros que analisaremos podem ser incluídos basicamente numa das três categorias: passa-baixas, passa altas, ou passa faixas, conforme deixem passar os sinais de baixas frequências, altas frequências ou uma faixa definida de frequências.
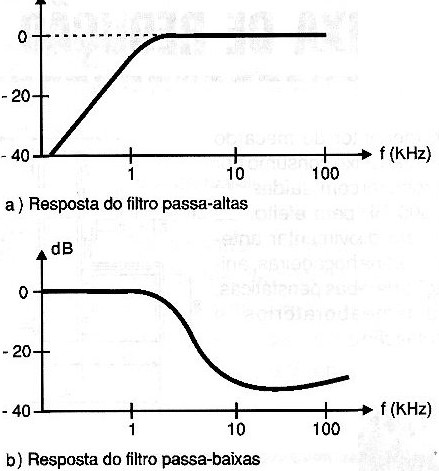
As curvas de respostas destes filtros estão representadas na figura 1.
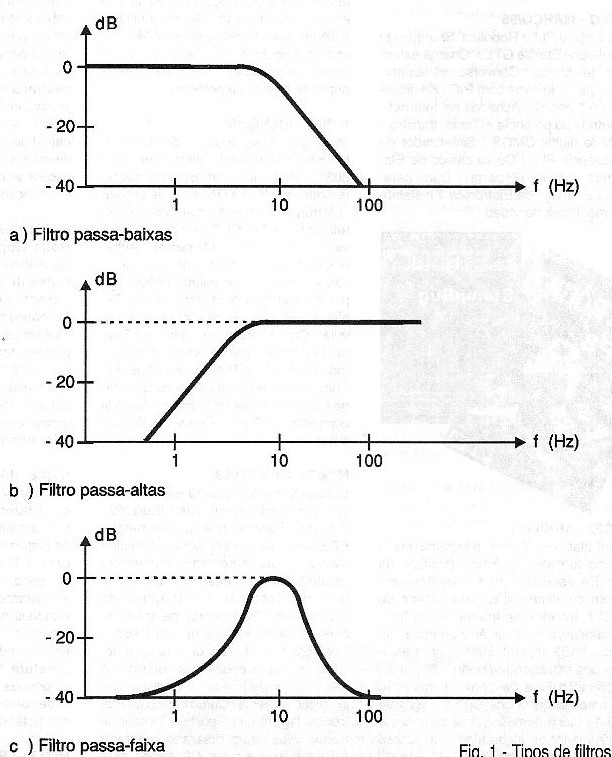
Observamos que em (a) por exemplo, temos um filtro passa-baixas em que todos os sinais abaixo de uma determinada frequência, denominada "corte", passam sem sofrer atenuação, enquanto que os demais são atenuados num grau que vai depender da configuração do filtro.
Na configuração os filtros são formados apenas por componentes passivos como resistores, capacitores e indutores de modo que os sinais passam sem sofrer nenhum tipo de amplificação.
Isso significa que estes filtros ou mantém os sinais numa determinada intensidade conforme sua frequência ou então os atenuam. Por este motivo, estes filtros são denominados passivos. Na figura 2 mostramos alguns tipos de filtros passivos bastante usados em aplicações práticas.
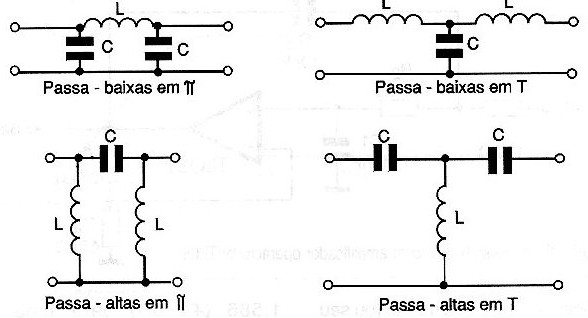
A combinação dos elementos de um filtro deste tipo com um circuito amplificador, como por exemplo usando amplificadores operacionais, acrescenta a configuração uma propriedade importante que é a de amplificar os sinais de determinadas frequências, ou pelo menos evitar que os sinais de certas frequências sofram fortes atenuações.
Isso nos leva a um tipo de filtro que apresenta um ganho real na potência do sinal que está sendo trabalhado. Estes filtros são denominados ativos.
Num filtro ativo temos um amplificador que pode adicionar energia ao sistema resultando ao mesmo tempo um efeito de filtragem e um ganho real de potência para os sinais que "passam" pelo circuito.
Outras vantagens podem ser apontadas nos filtros deste tipo como por exemplo a possibilidade de se modificar a impedância sem perdas, ou ainda de se associar diversas etapas de filtragem sem se obter uma queda muito grande da intensidade do sinal.
Funções de alto Q em baixas frequências podem então ser implementadas sem a necessidade de se usar indutores de valores muito altos como ocorreria se filtros passivos fossem usados.
Nos circuitos de baixa frequências esta não necessidade de indutores é muito importante pois estes componentes, quando tem valores altos são caros, pesados e volumosos.
Conforme a configuração os filtros podem ser projetados com características de atenuação que vão de 6 a 50 dB por oitava.
Dentre as principais vantagens apresentadas pelos filtros ativos com amplificadores operacionais destacamos as seguintes:
Não temos perdas por inserção. O sistema pode proporcionar ganho quando necessário.
Custo baixo. Os componentes usados nos filtros ativos são menores do que os equivalentes necessários nos circuitos passivos.
Melhor sintonia. Os filtros ativos podem ser facilmente sintonizados e ajustados numa ampla faixa de frequências sem alteração das curvas de resposta.
Melhor isolação: a elevada impedância de entrada dos circuitos e baixa impedância de saída faz com que haja um mínimo de interação entre os circuitos de entrada e saída e a própria carga.
A seguir damos alguns circuitos práticos de filtros ativos com as fórmulas para se calcular sua frequência de operação em função dos valores dos componentes usados.
FILTRO PASSA-FAIXA
Neste tipo de filtro temos a passagem de sinais numa determinada faixa ou banda de frequência, rejeitando os sinais de todas as outras frequências.
O equivalente passivo mais comum faz uso de um indutor e um capacitor (LC). No entanto, nas baixas frequências o projeto de um filtro deste tipo torna-se crítico devido à necessidade de se usar indutores de valores muito altos.
Utilizando um amplificador operacional temos a vantagem de poder implementar um filtro deste tipo sem a necessidade de usar indutores.
Na figura 3 temos um exemplo de filtro ativo bipolar tendo por base um amplificador operacional com FETs tipo TL081.
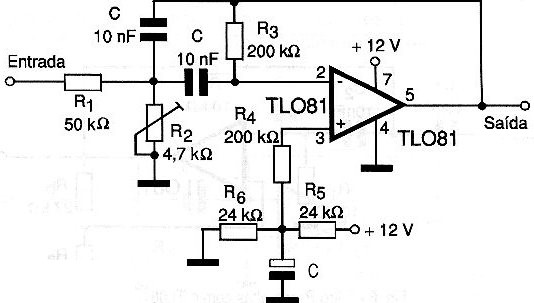
Este circuito é indicado para aplicações que exijam fatores Q menores que 10 e o ganho será ligeiramente maior do que a raiz quadrada do fator Q escolhido. Assim, para um fator Q igual a 5 termos um ganho de tensão pouco maior do que 2.
Os valores dos componentes para este filtro são calculados pelas seguintes fórmulas:
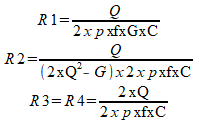
Onde:
f = frequência central do filtro em hertz (Hz)
Q = fator de qualidade
G = ganho de tensão
C = capacitância em farads (F)
Tomemos como exemplo o cálculo de um filtro que tenha por frequência central 800 Hz e que use como r2 um potenciômetro com duas vezes o valor calculado de modo a se poder ajustar precisamente a frequência. Este valor maior é sugerido para compensar as tolerâncias dos demais componentes.
Para a faixa de áudio os valores dos capacitores estão tipicamente entre 10 e 100 nF.
Considerando:
f = 800 Hz
Q = 5
G = 2
C = 10 nF
Temos:
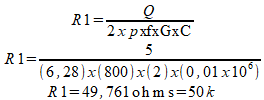
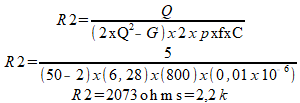
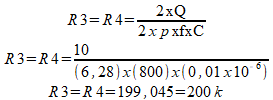
Na figura 4 temos a curva de resposta deste filtro. esta curva tem como referência uma tensão de entrada de 4,4 Vpp.
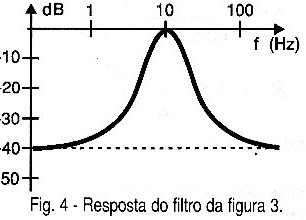
FILTRO PASSA-ALTAS E PASSA-BAIXAS
Dos muitos tipos de filtros que podem ser usados para deixar passar somente altas ou somente baixas frequências, o "Butterworth" é um dos melhores. Filtros complexos normalmente usam redes de primeira e segunda ordem. As redes de primeira ordem não são muito úteis porque só podemos controlar a frequência central, ao mesmo tempo em que, usando filtros de segunda ordem podemos controlar além da frequência central também a impedância e o amortecimento (ou seu inverso que é o fator Q).
Na figura 5 temos uma configuração simples que faz uso de um amplificador operacional como seguidor de tensão.
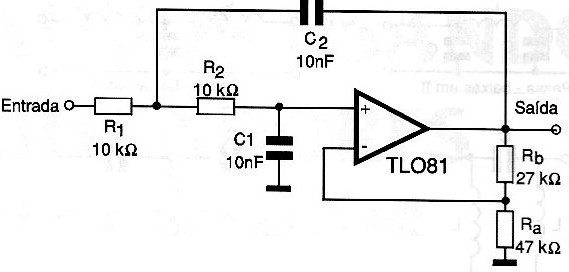
Neste circuito os capacitores apresentam um efeito muito pequeno nas baixas frequências o que resulta numa resposta plana nesta região do espectro. No entanto, nas altas frequências, os capacitores separadamente desviam o sinal para pontos de baixa impedância o que faz com que a resposta caia.
Um filtro de duas etapas faz com que a resposta nas altas frequências caia com o quadrado da frequência, daí o nome de "filtro de segunda ordem" para esta configuração.
A resposta começa plana nas frequências mais baixas para cair depois com atenuação de 12 dB por oitava inicialmente ou 40 dB por década passando a frequência de corte.
Uma boa aproximação para o cálculo deste tipo de filtro pode ser obtido com a fixação de R1 igual R2 e C1 igual a C2. Assim, a frequência de corte pode ser calculada por:
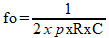
Temos aqui o filtro de "componentes iguais" com uma faixa passante de 1,586 (+4 dB) para uma rede Butterworth de segunda ordem, e este é o único ganho que faz com que o circuito funcione apropriadamente.
Como o amplificador operacional opera na configuração não inversora, o resistor de realimentação deve ser 0,586 vezes o valor do resistor de entrada RA de modo a se fixar o ganho em 1,586.
Para projetar um filtro passa-baixas com frequência de corte de 1500 Hz proceda da seguinte maneira:
Fixe RA em 47 kohms. RB deverá ser então RA x 0,586 ou aproximadamente 27kohms. Se fixarmos os capacitores em 10 nF, os resistores serão selecionados pela seguinte fórmula:
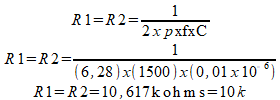
A simples troca de posição entre os resistores e os capacitores nos leva a um filtro passa-altas, que é mostrado na figura 6. O cálculo dos componentes e o ganho são os mesmos do circuito anterior.
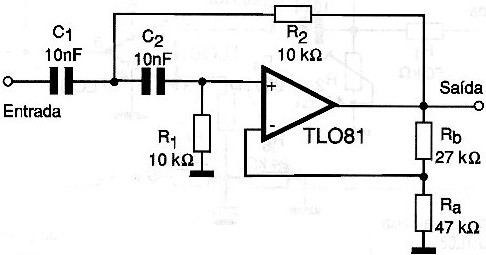
Na figura 7 temos as curvas de resposta em frequência para as duas versões.
FILTRO PASSA-FAIXA COM REALIMENTAÇÃO MÚLTIPLA
O filtro básico passa-faixa de múltiplo feedback ou realimentação é empregado quando se deseja um fator Q da ordem de 15 e um ganho "moderado".
A única dificuldade que podemos encontrar na utilização de tais filtros é que à medida que o fator Q aumenta, eles se tornam mais críticos, acentuando-se a dificuldade em se obter a sintonia correta.
A experiência mostra que filtros passa-faixas ativos de alta performance e alto Q não podem ser projetados eficientemente com um único amplificador operacional.
Assim, as versões com um único operacional são indicadas para os casos em que se necessita de baixos fatores Q (entre 2 e 5 tipicamente). Por sorte, valores nesta faixa são indicados em muitas aplicações práticas em áudio como por exemplo equalizadores, controles de tonalidade, etc.
Na figura 8 temos um circuito de uma única etapa de realimentação múltipla onde o amplificador operacional funciona como um inversor.
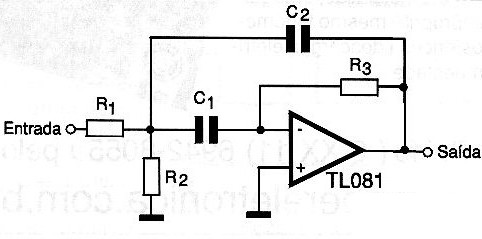
O resistor R3 ligado entre a saída e a entrada inversora fixa o ganho e a corrente através do capacitor C1, que por sua vez, determina a frequência de operação. O capacitor C2 proporciona a realimentação da saída para a junção de R1 com R2. Os capacitores C1 e C2 devem ser sempre do mesmo valor. O resistor R2 pode ser ajustável para se fazer a sintonia.
A frequência de operação é dada pela seguinte fórmula:
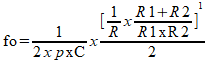
Ao projetar um filtro deste tipo parte-se de C1 e C2 com valores iguais, entre 10 e 100 nF para a faixa de áudio., o que resulta em valores razoáveis para os resistores.
Vamos supor o projeto de um filtro para 10 kHz com fator Q de 3 e um ganho 2.
Os três resistores são calculados pelas seguintes fórmulas:
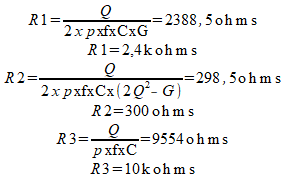
Nestas fórmulas temos:
G = ganho = 2
Q = fator de qualidade = 3
C = Capacitância = 10 nF
f = frequência = 10 kHz
FILTROS COM GIRADORES
Os giradores (gyrators) levam este nome pelo fato de seu princípio de funcionamento apresentar uma certa analogia com os giroscópios mecânicos.
Um girador pode se comportar como um indutor e num filtro ativo isso é importante, pois conforme explicamos no início do artigo, os indutores para baixas frequências devem ser evitados por serem pouco práticos como componentes.
Uma indutância apresenta uma impedância dada por:
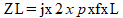
Onde:
ZL é a impedância em ohms
f é a frequência em hertz (Hz)
L é a indutância em Henry (H)
j é o operador imaginário que equivale a (raiz de -1), necessário pelo fato de haver uma rotação de fase na qual a corrente se adianta em relação à tensão.
Para simular uma indutância precisamos de um circuito que satisfaça esta equação. Na figura 9 mostramos um diagrama básico de tal circuito.
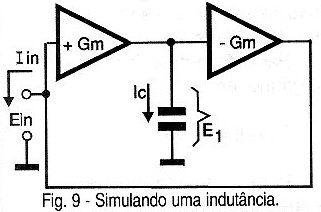
Os amplificadores A e B são do tipo "Operacional de Transcondutância" (OTA) que devem ser iguais, exceto pelo fato de que um deles serve para inverter a fase do sinal.
Para efeito de cálculo, supondo G o ganho temos:
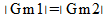
Para o circuito mostrado temos especificamente:
Iin=GmxE1 (I)
Zin=Ein/Iin (II)
Ein=-Ic/Gm (III)
Substituindo as equações I e III na equação II temos:
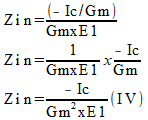
Mas, como Ic é dado por:
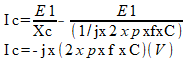
Substituindo a equação (V) na equação (IV) temos:
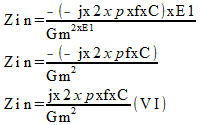
A equação (VI) pode ser melhorada se fizermos:
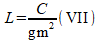
Rearranjando a equação chegaremos então à:
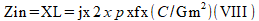
Esta equação corresponde justamente à de uma indutância, mas sem precisarmos usar um indutor "físico" no circuito. Isso significa que este circuito pode ser usado eficientemente para simular um indutor.




















