7.1 - O QUE SÃO OSCILADORES
Sons são produzidos quando uma corrente elétrica, que muda constantemente de sentido, ou ainda sofre variações periódicas de intensidade, circula através de um transdutor apropriado.
Como, por exemplo, podemos citar a cápsula de um fone ou um alto-falante. Para que tenhamos sons audíveis, a frequência desta corrente deve estar entre 15 e 15 000 Hertz aproximadamente, mas como existem animais que podem perceber frequências maiores, o espectro de áudio não é limitado somente por estes valores.
Em Eletrônica as frequências da faixa de áudio são aquelas que vão até aproximadamente 100 000 Hz, conforme o leitor poderá ver na figura abaixo.
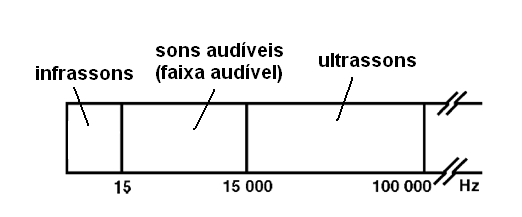
Por outro lado, para que tenhamos ondas de rádio ou ondas eletromagnéticas, é preciso que correntes também variáveis de frequências que podem ir de algumas dezenas de quilohertz, ou mesmo mais baixas, até bilhões de hertz, sejam aplicadas a uma antena. As frequências desta faixa formam o espectro das radiofrequências ou RF, conforme mostra a figura abaixo.
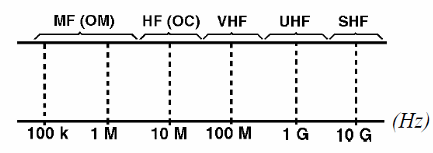
Para produzir correntes elétricas em frequências que correspondam tanto a faixa das áudio frequências (AF), como das rádio frequências (RF), são usados circuitos denominados osciladores.
Na documentação técnica inglesa é comum encontrar a abreviação LF para baixa frequência – low frequency e HF para alta frequência – high frequency).
Basicamente, um oscilador nada mais é do que um amplificador que é ligado de tal maneira que, em sua saída tenhamos um sinal com frequência e amplitude definidas.
As propriedades elétricas dos transistores bipolares permitem que estes componentes sejam usados em osciladores de diversos tipos. O modo como cada tipo de oscilador funciona, caracteriza seu tipo e existem muitos deles, dos quais veremos os principais nesta lição.
Para que um transistor oscile, a técnica usada é muito simples: tomamos o sinal amplificado na saída de um transistor usado como amplificador e o aplicamos de volta à sua entrada, ou seja, fazemos um circuito com realimentação positiva.
O sinal de saída volta para a entrada e, novamente é amplificado, resultando em novo sinal de saída que volta à entrada, num ciclo que dura indefinidamente (enquanto o circuito for alimentado), produzindo assim as oscilações, conforme o leitor verá na figura a seguir.
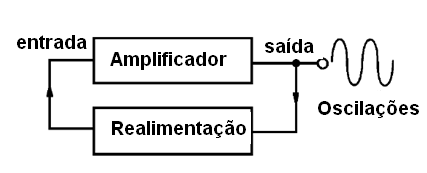
Temos um exemplo de como isso funciona quando ligamos um amplificador com um microfone ligado à entrada e abrimos o volume. O sinal do alto-falante é captado de volta pelo microfone, passando novamente pelo amplificador, num ciclo que produz um forte apito, ou realimentação acústica. Esse apito é denominado “microfonia”.
A velocidade com que o sinal é aplicado à entrada determina o tempo de percurso do sinal num ciclo completo e, portanto, a frequência de operação do oscilador.
Veja que é de fundamental importância que o “ganho” do amplificador seja maior que 1, ou seja, o sinal de saída deve ser “mais forte” que o de entrada.
Se tivermos um circuito com ganho menor que 1, o sinal de saída será mais fraco que o de entrada, e não mais conseguirá excitar o circuito com a mesma intensidade no ciclo seguinte, que se enfraquece um pouco mais.
O novo ciclo ainda mais fraco só dará origem a uma saída ainda menor. Isso significa que o sinal gerado vai então reduzindo de intensidade, dando origem ao que chamamos de “oscilação amortecida” até desaparecer, conforme poderemos observar na figura abaixo.
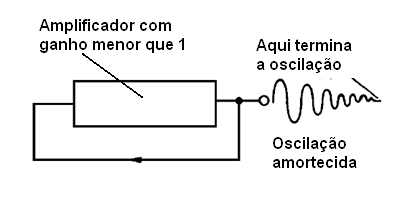
É evidente que um circuito com ganho exatamente de uma vez não serve para uma aplicação prática, pois não podemos “tirar” qualquer parcela do sinal para uso externo. Se isso for feito, já teremos um sinal mais fraco na entrada, e as oscilações amortecem.
Para que possamos usar o sinal gerado, é preciso que o ganho seja bem maior que um, de modo que “sobre” uma boa parte do sinal para uso externo.
Outra condição importante para se projetar um oscilador, é que o sinal aplicado na entrada tenha fase apropriada. Não basta ligar simplesmente a saída (coletor) de um transistor na configuração de emissor comum na sua entrada (base), conforme o leitor poderá ver na próxima figura, para que o circuito entre em oscilação.
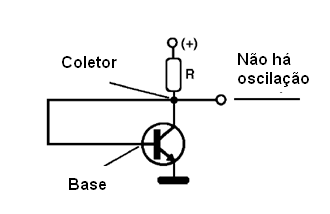
Conforme estudamos em lições anteriores, nesta configuração o transistor inverte a fase do sinal, o que significa que, para o circuito, o sinal reaplicado à entrada não provoca reforço, mas sim enfraquecimento do processo, e não há oscilação.
Num circuito como este, para haver oscilação ao se reaplicar o sinal à entrada, é preciso intercalar um sistema qualquer que inverta a fase do sinal. Veja na figura abaixo para saber como isso deve ser feito.
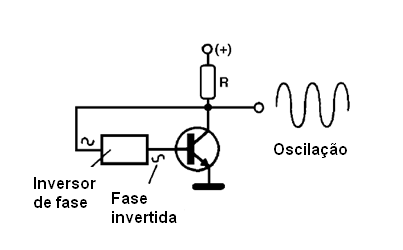
O sistema que inverte a fase do sinal, também é responsável por um retardo. Esse retardo pode então ser calculado de modo que o sinal percorra o circuito num tempo desejado, determinando assim a frequência do sinal que vai ser gerado.
As redes de realimentação, conforme são chamadas, podem ser de diversos tipos, existindo cálculos que possibilitam calcular a sua frequência de operação.
O tipo de sinal gerado, ou seja, sua forma de onda, também dependerá do modo como a realimentação é feita. Conforme veremos, ao estudar os diversos tipos de osciladores, os sinais gerados podem ter as mais diversas formas de onda, sendo as mais comuns as senoidais, retangulares, dente de serra e triangulares.
E também, conforme veremos a seguir, os diversos tipos de osciladores se diferenciam segundo a forma como o sinal é retirado da saída e reaplicado à entrada, e também como ocorrem as inversões de fase quando necessárias. Também veremos que todos os osciladores têm suas limitações, o que os torna aplicáveis em determinadas faixas de frequências e aplicações.
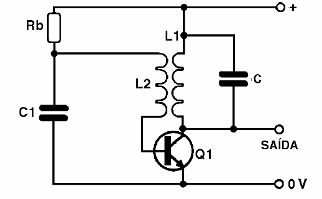
7.2 – Oscilador Hartley
Este é um tipo de oscilador LC, ou seja, em que a frequência do sinal produzido é determinada por uma bobina e um capacitor. Veja na próxima figura a configuração básica deste oscilador, observando-se que a bobina possui uma tomada ou derivação.
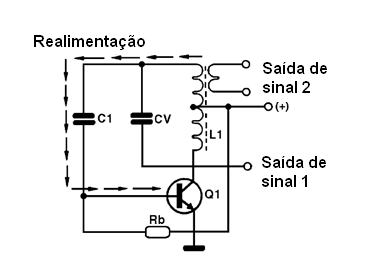
O resistor Rb faz a polarização da base do transistor e o capacitor C1 faz a realimentação, ou seja, “joga” parte do sinal obtido na saída para a entrada do circuito. O funcionamento deste oscilador é o seguinte:
Quando ligamos o circuito, o resistor polariza a base do transistor próxima da saturação, havendo então sua condução. Uma forte corrente circula entre o coletor e a fonte de alimentação, ligada à tomada central, pela bobina L1.
O resultado é que esta corrente em L1 induz na outra metade da mesma bobina uma corrente a qual é aplicada novamente à base do transistor, através do capacitor C1. O sentido de circulação desta corrente é tal que, o transistor é levado quase ao corte. Como resultado, a corrente de coletor cai e, portanto, em L1, com um efeito que reduz a indução da corrente na outra metade da mesma bobina e, portanto, através de C1 e da base do transistor.
Com isso, novamente temos a predominância da polarização pelo resistor, que faz o transistor conduzir e um novo ciclo tem início. O transistor fica então neste “vai e vem” entre o corte e a saturação, produzindo-se um sinal cuja frequência é determinada pela bobina e pelo capacitor em paralelo, já que a indução que vimos também leva em conta a carga e descarga do capacitor CV.
O sinal deste oscilador pode ser retirado tanto do coletor do transistor como de um enrolamento adicional feito sobre L1. Este tipo de oscilador pode ser usado para produzir sinais e frequências que vão de alguns hertz (áudio) até algumas dezenas de megahertz (RF). A principal limitação que encontramos para este tipo de oscilador quando operando na faixa de áudio, é que precisamos de bobina de grande indutância.
Fórmula Para a Frequência do Oscilador Hartley
Num oscilador Hartley a realimentação é feita pela bobina de carga L. Este tipo de circuito funciona até algumas dezenas de Megahertz. A frequência de um oscilador Hartley é dada pelo circuito ressonante LC como mostra a figura abaixo.
Formula f7.1
f =
1
2 x π x √ (L x C)|
Onde:
f é a frequência em hertz (Hz)
L é a indutância em Henry (H)
C é a capacitância em Farads (F)
π é 3.1416
7.3 - OSCILADOR COLPITTS
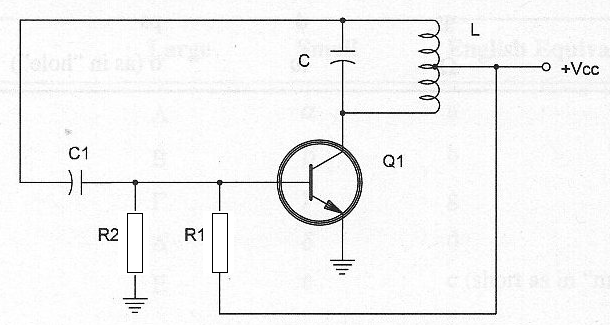
O oscilador Colpitts, tem um princípio de funcionamento bastante semelhante ao oscilador Hartley, com a única diferença de que o sinal para a realimentação positiva é retirado numa derivação feita com base em capacitores, conforme mostra a figura abaixo.
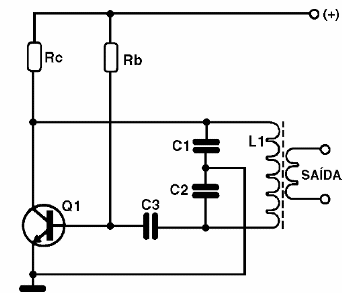
O transistor se mantém em condução durante os semiciclos positivos do sinal, e é levado próximo ao corte nos semiciclos negativos. Veja que a frequência é dada pela bobina L1 e pelos capacitores em paralelo.
Este circuito opera em uma faixa de frequências que vai de alguns hertz até algumas dezenas de megahertz.
Observamos que, tanto para o caso de transistores no oscilador Hartley, como Colpitts, além de outros componentes semicondutores, é possível a construção de configuração equivalente com válvulas. O sinal gerado por este circuito pode ser, tanto retirado do coletor do transistor, como a partir de um enrolamento, formando um secundário do transformador, conforme o leitor poderá ver clicando na figura abaixo.
Oscilador de Colpitts
No oscilador de Colpitts ou simplesmente, oscilador Colpitts, a realimentação é feita por um divisor capacitivo, como mostrado na figura 226. A frequência também depende do circuito LC, e a fórmula para calcular esta frequência é dada a seguir.
Fórmula:
f =
1
2 x π x √ (L x C)|
Onde :
f é a frequência em hertz (Hz)
π é a constante 3.1416
C é a capacitância em Farads (F)
L é a indutância em Henry (H)
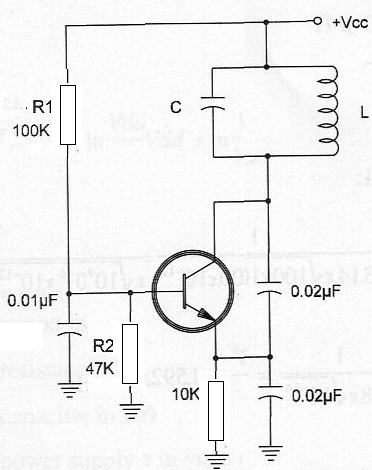
7.4 - OSCILADOR DE BLOQUEIO
Uma configuração bastante importante usada como oscilador com transistores bipolares pode ser vista na figura abaixo. Ela consiste num oscilador de bloqueio, com um transistor na configuração de emissor comum.
Veja que estamos dando como exemplos configurações que fazem uso de transistores comuns. Essas mesmas configurações, entretanto, encontram equivalentes com válvulas e outros tipos de componentes.
O coletor do transistor é ligado ao enrolamento primário de um transformador cujo secundário corresponde ao circuito de realimentação. O secundário está ligado a base do transistor. O transistor é polarizado próximo ao ponto de saturação pela ligação do resistor Rb.
Quando ligamos a alimentação, o resistor polariza a base do transistor que conduz produzindo um pulso de corrente no primário do transformador (L1).
Este pulso induz no secundário uma corrente que se opõe a polarização de Rb, levando o transistor ao corte. Com isso o transistor “desliga” e, novamente entra em ação a polarização do resistor fazendo com que novo pulso seja produzido no coletor. O capacitor C1 controla tanto a corrente de polarização, carregando-se com ela, como a que se opõem, descarregando-se e determinando assim a frequência de operação juntamente com C.
A frequência de operação é determinada também pela indutância da bobina e pelo capacitor em paralelo. Veja que este circuito deve ser “disparado” por um pulso externo, mas existem versões que são “autodisparadas”, ou seja, entram em funcionamento quando a alimentação é estabelecida.
As versões que precisam ser disparadas externamente são muito usadas em televisores, para a elaboração dos circuitos de sincronismos em que um sinal externo controla o oscilador, que é responsável pela manutenção da estabilidade da imagem. O mesmo circuito pode ser feito com um transistor ligado na configuração de base comum, conforme mostra a figura abaixo.
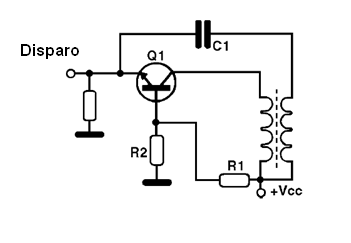
Veja então que o sinal é retirado do coletor e reaplicado ao emissor, havendo uma polarização fixa na base do transistor. O pulso de disparo é aplicado à base. Estes circuitos podem ser usados em frequências que vão de alguns hertz até algumas dezenas de megahertz. Na próxima figura temos a forma de onda típica produzida por um oscilador deste tipo.
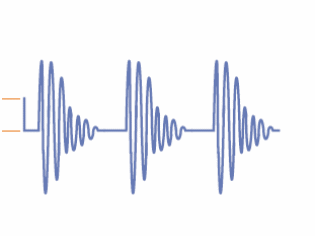
A frequência deste circuito é calculada da mesma forma que nos circuitos anteriores, pelo circuito ressnante LC no coletor do transistor.
7.5 - OSCILADOR DE DUPLO T
O nome deste oscilador se deve à rede de realimentação que proporciona uma inversão de fase do sinal e que usa apenas resistores e capacitores, conforme o leitor poderá ver na figura abaixo.
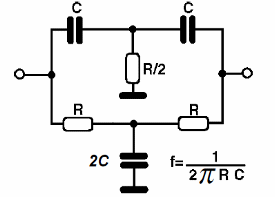
Para que o duplo T funcione, proporcionando a inversão de fase desejada, os componentes que o formam devem manter uma relação bem definida de valores.
Assim:
R1 = R2 = 2 x R3
C1 = C2 = C3/2
A frequência de operação do oscilador é dada pela fórmula:
f =
1
2 x π x R x C
Onde
R = R1 = R2 - resistência em ohms (ohms)
C = C1 = C2 - capacitância em farads
π = 3,14 (constante)
f = frequência em hertz
Na figura abaixo, temos a configuração de um oscilador de duplo T completo, com um transistor na configuração de emissor comum.
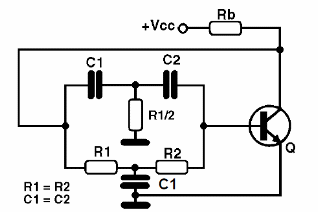
Os capacitores devem ser selecionados de acordo com a frequência de operação desejada. Podemos alterar levemente a frequência do oscilador, e até obter oscilações amortecidas com a utilização de um trimpot ou potenciômetro para R3, conforme mostra a figura abaixo.
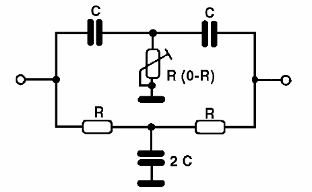
Na próxima figura oscilações amortecidas produzidas por um oscilador deste tipo.
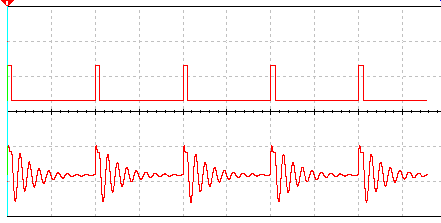
Este oscilador se presta principalmente para a produção de sinais na faixa de áudio. É importante observar que as formas de onda dos sinais dos osciladores dependem bastante das configurações.
Normalmente procura-se gerar sinais senoidais em todas as versões que vimos, mas dependendo das características dos componentes usados, podem ocorrer deformações. Para o caso do oscilador de duplo T o sinal é senoidal.
7.6 – Oscilador por Deslocamento de Fase
Neste tipo de oscilador, temos a rede de resistores e capacitores que formam o circuito de realimentação, deslocando em 180 graus a fase do sinal. Desta forma, temos a inversão de fase necessária a manutenção das oscilações. Veja a figura seguinte, onde temos um circuito de oscilador de deslocamento de fase com um transistor.
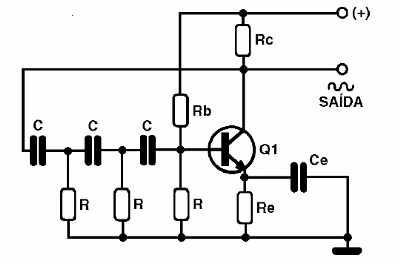
A frequência de operação deste oscilador é dada pela fórmula:
f =
1
2 x π x √ (6 x R x C)|
Onde:
f é a frequência de operação em Hertz
π é constante, valendo 3,14
R é o valor dos resistores usados nas células em ohms
C é o valor dos capacitores usados nas células em farads.
Neste circuito, cada resistor, em conjunto com um capacitor, desloca em 60 graus a fase do sinal, de modo que, com 3 células, temos um deslocamento de 180 graus na fase do sinal, ou seja, obtemos sua inversão.
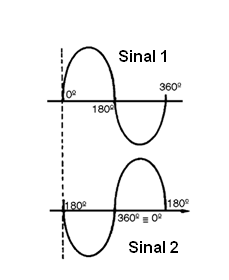
Para os leitores não familiarizados com esta forma de especificação da fase fazemos uma observação: O que ocorre, é que um ciclo completo de um sinal, corresponde a uma volta completa de um gerador “imaginário” que o produz, conforme o leitor poderá ver na próxima figura. (Veja o volume ou curso anterior Eletrônica Básica).
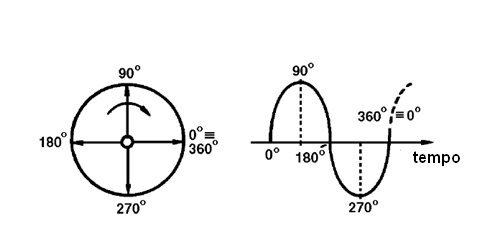
Assim, uma volta completa do gerador, ou seja, um ciclo completo corresponde a 360 graus. Quando os dois sinais estão no mesmo ponto da “volta imaginária”, ou seja, de um ciclo, dizemos que eles estão em fase.
Se a diferença de posição destes sinais for tal que tenhamos 1/4 de volta, ou 90 graus, conforme mostra a figura a seguir, dizemos que estes sinais estão em quadratura.
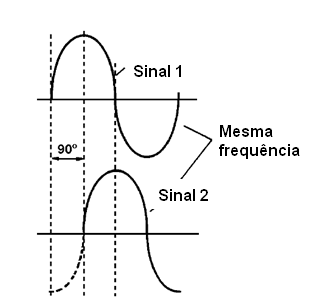
Por outro lado, se a diferença dos pontos for tal, que tenhamos meia volta, ou seja, 180 graus, o que quer dizer que, quando um estiver no máximo positivo o outro estará no máximo negativo, dizemos que estes sinais estão em oposição de fase ou com as fases invertidas, conforme o leitor poderá verificar na figura abaixo.
Os osciladores por deslocamento de fase são usados apenas para produzir sinais de frequências na faixa de áudio.
7.7 - MULTIVIBRADOR ASTÁVEL
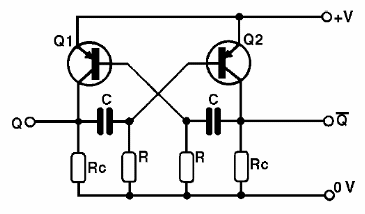
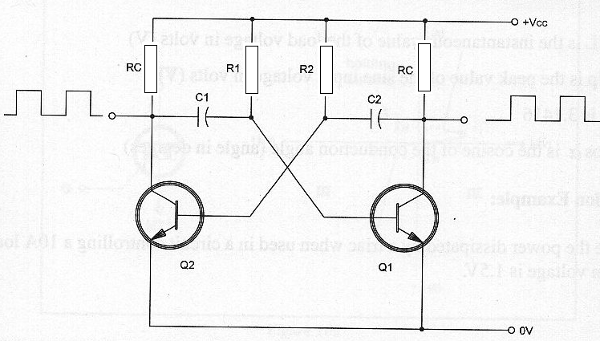
Chegamos agora a uma configuração que produz sinais de maneira muito especial, pois além dos sinais terem uma forma de onda retangular, são utilizados dois transistores. Na figura abaixo temos a configuração básica de um multivibrador astável com dois transistores NPN. Esta mesma configuração pode ser obtida com transistores PNP, transistores de efeito de campo, válvulas e outros componentes ativos.
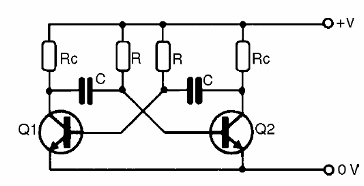
Os dois transistores são ligados de tal forma que, a cada instante, quando um está no corte o outro estará obrigatoriamente saturado, ou seja, apenas um dos transistores pode conduzir de cada vez. Podemos comparar este circuito a uma gangorra que, quando um lado “sobe” o outro obrigatoriamente “desce”, conforme sugere a figura abaixo.
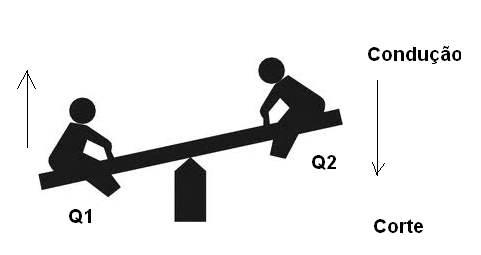
No multivibrador astável, conforme o nome sugere, a condução dos transistores não é uma situação estável, de modo que cada transistor só pode ficar por tempo limitado nesta condição.
Isso faz com que os dois transistores do circuito fiquem constantemente trocando de estado, passando do corte para a saturação, e vice-versa, numa velocidade que depende dos componentes usados, conforme o leitor poderá constatar pela figura a seguir.
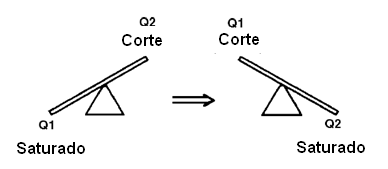
Tomando como base o circuito da figura, vejamos como ele funciona: ao estabelecermos a alimentação os dois transistores são polarizados de modo a irem à saturação pelos resistores de base. No entanto, devido a diferença de características, um deles conduz mais que o outro e logo satura. Com isso, o outro transistor é impedido de conduzir e permanece no corte.
Supondo que Q1 vá a saturação e Q2 volte para o corte, o capacitor C1 começa a se carregar através do resistor R1 até o instante em que alcança-se uma tensão suficiente para polarizar Q2 no sentido de fazê-lo conduzir. Quando isso ocorre o circuito comuta e Q1 passa ao corte enquanto que Q2 vai a saturação.
Neste momento, é C2 que começa a se carregar através de R2 até que o transistor Q1 seja levado à condução. O circuito ficará trocando de estado por tempo indeterminado (enquanto houver alimentação), numa velocidade que dependerá dos valores dos capacitores e dos resistores usados.
Como a comutação dos transistores ocorre de forma muito rápida, o sinal produzido tem forma de onda retangular. Veja que podemos retirar o sinal do circuito tanto do coletor de Q1, como do coletor de Q2.
No entanto, estes sinais estarão com níveis diferentes. Assim, nos instantes em que a tensão do coletor de Q1 estiver próxima do positivo da alimentação (corte), ou seja, tivermos um nível alto de tensão, no coletor de Q2, que estará em zero (saturação), teremos um nível baixo de tensão.
Dizemos que as saídas são complementares e as representamos por Q e Q. A barra sobre o Q indica a situação complementar. Se os capacitores e os resistores usados forem iguais, o tempo de condução e corte de cada transistor será o mesmo, e teremos então um sinal “quadrado”, ou seja, com tempos de nível alto e baixo iguais, conforme o leitor poderá ver na figura abaixo.
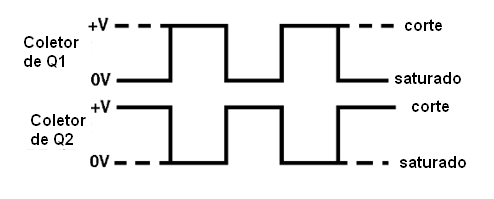
A frequência de um multivibrador astável será tanto maior quanto menores forem os capacitores usados. Na prática, com transistores comuns, o limite superior para a frequência de operação deste circuito está em torno de 5 MHz. No entanto, com transistores muito rápidos, pode-se conseguir frequências que chegam aos 100 MHz.
Na próxima figura, onde temos a versão do multivibrador astável com transistores PNP, observando-se que invertem-se apenas os sentidos de circulação das correntes.
Os multivibradores astáveis são muito usados em circuitos lógicos que, conforme já explicamos, admitem dois níveis de tensão apenas. Eles funcionam como cadenciadores, relógios ou “clocks”, determinando o ritmo ou velocidade de sua operação.
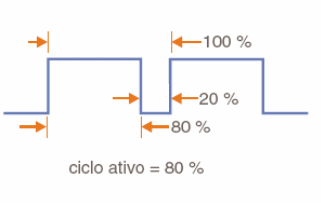
Ciclo Ativo
Para um sinal retangular de determinado período, o tempo em que ele permanece no nível alto, somado ao tempo que ele permanece no nível baixo resultam o período total. No entanto, os sinais podem ser assimétricos em relação a esses dois tempos. Quando o tempo no nível alto é igual ao tempo no nível baixo, conforme mostra a próxima figura, dizemos que se trata de um sinal “quadrado”, se bem que essa denominação não seja muito criteriosa no sentido de que as unidades no sentido vertical são amplitudes e no sentido horizontal são tempos.
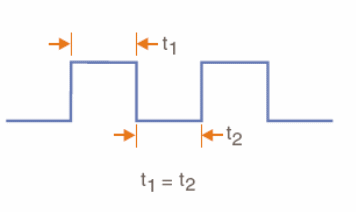
Para sinais em que os tempos no nível alto e baixo são diferentes, podemos falar em ciclo ativo, e definir o ciclo ativo como a porcentagem do tempo total do ciclo em que o sinal permanece no nível alto, conforme mostra a figura abaixo.
Cálculo da Frequência do Multivibrador Astável
Para o circuito da figura abaixo, podemos calcular a frequência pelas fórmulas que são dadas a seguir.
Fórmula:
Tempo de condução:
tp = 0.69 x R x C
Onde:
tp é o tempo de condução de um transistor em segundos (s)
R é a resistência em ohm (ohms)
C é a capacitância em Farads (F)
Fórmula:
Frequência:
f =
1
tp1 + tp2
f =
1
0.69 x (R1 x C1 + R2 x C2)
Onde:
f é a frequência em hertz (Hz)
R1, R2 são as resistências em ohm (ohms)
C1, C2 são as capacitâncias em Farads (F)
Formulas derivadas:
Formula:
Oscilador quadrado (50% de ciclo ativo) - R1=R2=R e C1=C2=C
f =
1
1,38 x R x C
Onde:
f é a frequência em hertz (Hz)
R é a resistência em ohm (ohms)
C é a capacitância em Farads (F)
Formula:
Frequência como função de C quando R1=R2=R e C1=C2=C.
f =
1
2 x tp
Onde:
f é a frequência em hertz (Hz)
tp é o tempo de condução em segundos (s)
7.8 - Harmônicas
Abrimos um pequeno parêntese neste ponto de nosso curso, para tratar um pouco deste assunto que é relacionado com as formas de onda produzidas pelos osciladores. Um matemático francês chamado Fourier, no século XIX, demonstrou, através de cálculos, que poderíamos obter qualquer forma de função periódica pela simples combinação de maneira apropriada de uma única forma de função que é a senóide.
Desta forma, até mesmo um sinal retangular, (que pode ser descrito por funções periódicas) pode ser “sintetizado”, simplesmente usando senóides, que são as formas “puras” ou fundamentais de onda, conforme mostra a figura abaixo.
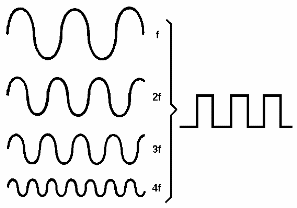
Assim, o que se faz é combinar a forma de onda de frequência que desejamos gerar, ou seja, a fundamental, com senóides de frequências que sejam múltiplas, ou seja, o dobro, o triplo, o quádruplo, etc., desta frequência fundamental. Estas frequências múltiplas são denominadas “harmônicas”, conforme o leitor poderá ver na próxima figura.
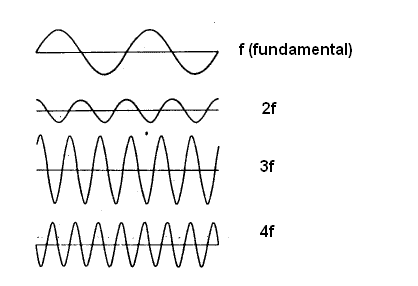
O interessante na eletrônica é que, quando temos um sinal ou uma forma de onda que seja complexa (não senoidal simplesmente), ela se comporta como realmente possuindo uma frequência fundamental e harmônicas de intensidades que vão decrescendo à medida que sua frequência aumenta, e isso até o infinito!
Assim, no caso de um multivibrador astável, que é uma forma de oscilador que gera um sinal particularmente rico em harmônicas, mesmo operando em frequências baixas, suas harmônicas se estendem a frequências muito altas, e por isso podem ser usadas também em aplicações práticas.
Um oscilador deste tipo que opere em apenas 1 kHz por exemplo, tem harmônicas suficientemente fortes em 1 MHz para poder excitar um rádio transistorizado e assim ser usado como injetor de sinais.
7.9 - OSCILADOR DE RELAXAÇÃO
Existem componentes que são mais apropriados que os transistores comuns para o projeto dos chamados osciladores de relaxação, mas é interessante também estudarmos este tipo de aplicação, já que ela servirá de boa base para as próximas lições. Na próxima figura temos o circuito básico de um oscilador de relaxação com dois transistores.
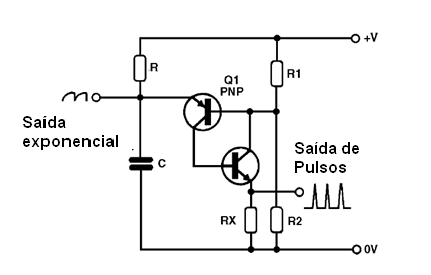
Os dois transistores são ligados de modo a formar uma chave regenerativa, ou seja, um circuito que realimenta a si próprio.
Ligamos então na entrada deste transistor uma rede de tempo RC e polarizamos a outra entrada de modo fixo, com um divisor com dois resistores. O transistor PNP tem sua base polarizada de modo a deixá-lo perto da plena condução.
Quando a tensão no capacitor sobe, à medida que ele se carrega através do resistor R, o transistor PNP aumenta sua condução, e com isso a base do transistor NPN é polarizada no sentido de também fazê-lo aumentar sua condução.
O resultado do aumento da corrente de base do transistor NPN é uma polarização maior da base do transistor PNP, num processo de realimentação: a tensão de base maior do PNP provoca novamente um aumento da corrente do NPN.
Partindo do instante em que o capacitor está descarregado, existe então um instante em que a tensão nas suas armaduras faz com que este processo de realimentação ocorra rapidamente, levando os dois transistores à saturação.
Chegamos então ao ponto em que o capacitor é curtocircuitado à terra e se descarrega com a produção de um pulso de corrente. Após o pulso, os transistores desligam e o capacitor começa a se carregar novamente, até ser novamente atingido novo ponto de disparo.
O circuito produz então um “trem de pulsos” cuja frequência depende da velocidade de carga do capacitor através do resistor. No capacitor, temos, então uma forma de onda exponencial, conforme temos na próxima figura.
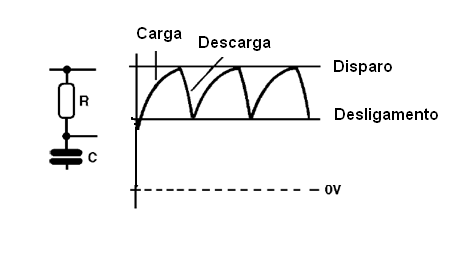
Este circuito é utilizado para gerar apenas sinais de freqüências relativamente baixas, na faixa que vai entre 0,01 Hz até 10 000 Hz ou pouco mais.
Oscilador de Relaxação com Lâmpada Neon
Um componente utilizado amplamente na elaboração de osciladores de relaxação é a lâmpada neon. Este componente apresenta uma característica de resistência negativa, ou seja, quando a tensão aplicada atinge certo valor, ele dispara e sua resistência cai.
A lâmpada neon pode ser usada para produzir sinais dente de serra na faixa de até algumas dezenas de quilohertz. O único inconveniente deste componente é que a tensão de disparo de uma lâmpada neon é muito alta, da ordem de 70 V e a tensão em que ela desliga, uma vez dispara é da ordem de 50 V.
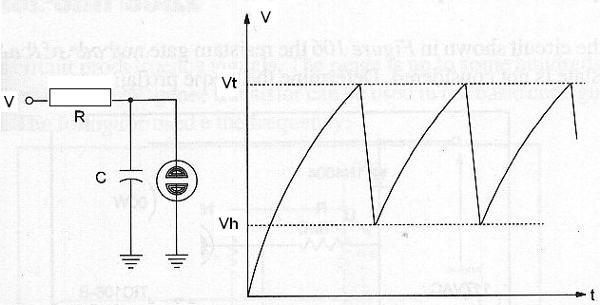
Sabemos que num circuito RC, o capacitor carrega-se exponencialmente quando aplicamos uma tensão. Se ligarmos uma lâmpada neon em paralelo com ele, quando for atingida a tensão de disparo, ele conduz, descarregando o capacitor até a tensão de manutenção, quando ela desliga.
Um novo ciclo de carga tem então início, produzindo-se assim uma forma de onda dente de serra.
A próxima figura mostra a configuração básica de um oscilador de relaxação usando uma lâmpada neon. Este circuito é indicado para frequências de fração de hertz até alguns quilohertz e opera com tensões a partir de 80 V.
Uma lâmpada neon típica dispara com 70 V e com isso acende. Se a tensão for reduzida para algo em torno de 50 V a lâmpada apaga e deixa de conduzir a corrente. A fórmula seguinte é válida para estes parâmetros.
Formula:
Período:
T = R x C x ln (
V - Vh
V - Vt
)
Onde
T é o período em segundos (s)
C é a capacitância em Farads (F)
R é a resistência em ohm (ohms)
V é a tensão de alimentação em volts (V)
Vt é a tensão de disparo em volts (V) - 70 V typ.
Vh é a tensão de manutenção em volts (V) - 60 V typ.
Formula:
Frequência:
f =
1
R x C x ln(
V - Vh
V - Vt
)
Onde :
f é a frequência em hertz (Hz)
C é a capacitância em Farads (F)
V é a tensão de alimentação em volts (V)
Vt é a tensão de disparo em volts (V)
Vh é a tensão de manutenção em volts (V)
O procedimento para uso da fórmula é o mesmo do oscilador de relaxação com transistor unijunção, descrito nesta seção.
7.10 - OUTROS OSCILADORES
Um tipo interessante de oscilador pela sua simplicidade e pela sua capacidade de excitar saídas com boa potência é o visto na figura abaixo.
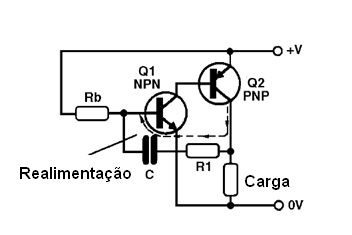
Este oscilador utiliza dois transistores complementares, ou seja, um NPN e um PNP formando uma etapa amplificadora de acoplamento direto. A realimentação de sinal que é responsável pelas oscilações é feita retirando-se o sinal diretamente da carga (coletor do transistor PNP), e reaplicando-se à base do transistor por meio de um capacitor em série com um resistor.
O resistor que polariza a base do primeiro transistor leva-o à condução, e com isso também o segundo transistor, que logo tem uma elevação da tensão em seu coletor. Esta elevação faz com que um pulso de corrente seja produzido através do capacitor, levando por um momento o transistor NPN (primeiro) perto do corte.
Cessando a condução deste transistor por um instante também cessa a condução do segundo, e um novo ciclo, com a atuação do resistor de base do primeiro transistor, se inicia. A frequência de operação deste oscilador é então determinada tanto pelo valor do resistor de polarização de base do primeiro transistor como pelo valor do capacitor no circuito de realimentação.
Outros osciladores importantes:
Oscilador Pierce
Oscilador Ponte de Wien
Oscilador de Clapp
7.11 – Controle de frequência
A frequência de um oscilador pode ser modificada com a utilização de um elemento que influa nesta grandeza e que possa ter seu valor alterado externamente. Podemos então usar indutores, capacitores e resistores variáveis para esta finalidade.
No caso de osciladores de altas frequências como os do tipo Hartley, Colpitts, de bloqueio, podemos ter indutores com núcleos variáveis (ajustáveis) ou então capacitores variáveis, dependendo da faixa de frequência que queremos “varrer”, conforme mostra a figura abaixo.
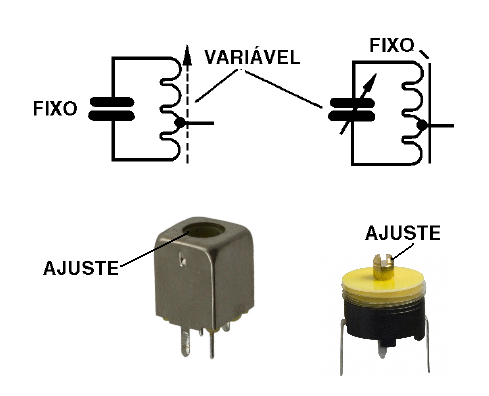
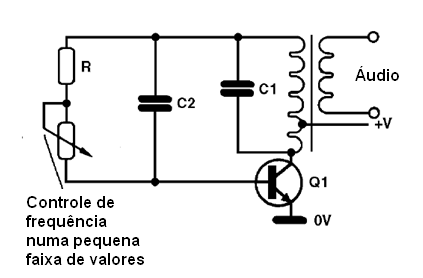
No caso de osciladores de frequências mais baixas, ou do tipo RC, é comum o uso de potenciômetros ou trimpots, já que, os capacitores usados são normalmente fixos, dado seu valor elevado. Na próxima figura temos o modo de se variar a frequência de forma sensível, atuando sobre a polarização de base de um transistor num oscilador Hartley.
Na próxima figura o leitor verá um modo de se variar a freqüência, e também o ciclo ativo, num multivibrador astável. Veja que, em todos os casos que usamos potenciômetros ou trimpots, atuamos sobre a polarização, de modo que precisamos sempre tomar cuidado em manter a faixa de valores da resistência apresentada dentro do que o transistor admite para oscilação.
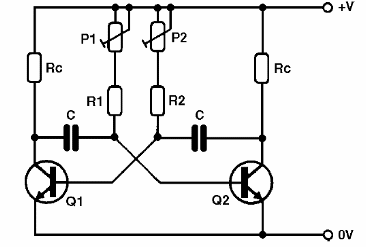
No caso do oscilador Hartley, por exemplo, pode haver “faixas mortas” em que as oscilações não ocorrem, o mesmo ocorrendo em relação ao multivibrador.
7.12 – Base comum
Uma característica dos osciladores na configuração de base comum, é que os transistores apresentam uma capacitância de entrada muito menor, influindo assim muito pouco na velocidade máxima em que eles conseguem operar. Desta forma, nesta configuração, podemos facilmente elaborar osciladores que alcançam centenas de megahertz, como o que pode ser visto na figura abaixo.
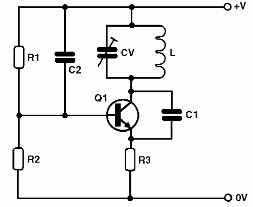
Este oscilador tem sua frequência dada pelo circuito LC, e a realimentação é obtida “pegando-se” o sinal do coletor e jogando-o ao emissor através do capacitor ligado entre estes dois elementos. Circuitos como este, são muito usados em transmissores para mais de 20 MHz, receptores super-regenerativos e conversores.
ÍNDICE
Parte 7 (Você está aqui)



















