No Monte um Computador Analógico (ART3212) ensinamos como montar um computador com potenciômetros e alguns componentes adicionais, cujo potencial de cálculo surpreendeu a muitos de nossos leitores. Nós mesmos temos o protótipo ainda montado o qual montamos num vídeo (veja no final do artigo o link). Demos exemplos de diversos cálculos e até fizemos um curso que mostrava como usar este computador (Computação Analógica – Lição 1 – Os Computadores Analógicos (CUR6001) ). No artigo anterior fomos um pouco além mostrando alguns cálculos avançados que podem ser feitos com o computador analógico. Neste artigo continuamos como mais alguns cálculos interessantes que, certamente, muitos dos nossos leitores não poderiam imaginar que poderiam ser feitos com ele.
Sugerimos que os leitores vejam os artigos indicados na introdução e também Cálculos avançados com um computador analógico - 1 (DID021)para saber um pouco mais sobre o nosso computador analógico.
Juros compostos
Não são apenas os cálculos de matemática pura ou ciências físicas que podem ser realizados com nosso computador analógico. Podemos ir além com cálculos de economia.
Dizer que o dinheiro em um banco rende juros compostos de 3% anualmente significa que no final de a cada ano sua conta aumenta em 3% da importância que estava no banco no início do ano. Por isso, se você depositou $ 100,00, no final do primeiro ano você teria 103,00 (100 + 3). No próximo anos você obteria 3% de 103,00 como juros. Isto ascende a 3,09. Assim, ao final de dois anos você teria 103,00 mais 3,09 ou 106,09.
Quanto você teria depois de 10 anos, 20 anos, 100 anos? Você pode ver que seria bastante trabalhoso descobrir isso por um longo período de tempo por
meios de cálculos da aritmética comum.
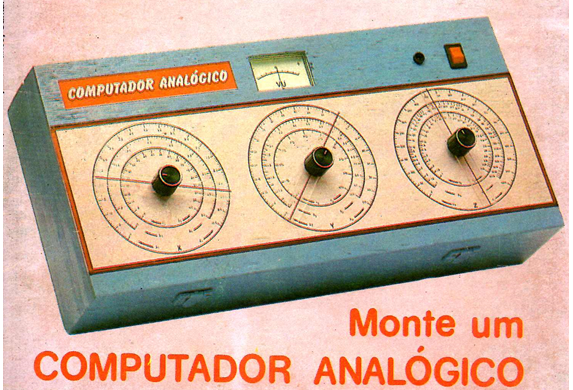
As escalas G, H e I nos potenciômetros X, Y e Z permitem que você obtenha estimativas rápidas. Por exemplo, quanto 1,00 renderia em 25 anos com juros de 4%?
Na figura 1 temos o modo de se fazer isso no computador analógico.
Defina a escala G no número 25 (número de períodos, em neste caso, anos).
Defina a escala H com 4% de juros.
A resposta é encontrada na escala I da maneira usual, girando o ponteiro até que o medidor leia zero quando o botão é pressionado. Neste caso, a resposta correta é 2,67. Você encontrará sua resposta em algum lugar em aquela região.
Observe que o cálculo é para um valor inicial (chamado de principal) de 1,00. Se você tivesse um valor investido de 100,00 o valor final seria 100 vezes 2,67 ou 267,00.
Agora tente este problema. Qual é montante obtido de 1,00 no banco com juros de 4% compostos semestralmente por 30 anos? Neste caso, devemos encontrar o juros a cada semestre. Por meio ano o montante seria a metade disso por um ano inteiro. Então o a taxa seria de 2% em vez de 4%. Mas em 30 anos teríamos que calcular os juros 60 vezes em vez disso de 30 (60 semestres).
Para resolver este problema, ajuste a escala G no potenciômetro X em 60. Defina os juros de 2% na escala H do potenciômetro Y. Encontre a resposta na escala I do potenciômetro Z.
Ela estará em algum lugar próximo 3,28. Para resolver um problema de juros compostos, defina o número de períodos de juros na escala G do potenciômetro X. A taxa de juros do período na escala H do potenciômetro Y.
Encontre o valor final na escala I do potenciômetro Z, da maneira usual.
Por que isso funciona?
A fórmula para o valor (A) de 1 com uma taxa de juros (i) por vários períodos de tempo (n) é dada pela fórmula:
A = (1 + i)
Tomando o logaritmo de ambos os lados, obtemos:
log A = n. log (1 + i)
Isso se assemelha à função X Y = Z em que n multiplicado por uma função de i, produz uma função de A . Portanto, podemos colocá-lo nas nossas escalas, desde que o façamos corretamente. Observe que G do potenciômetro X foi marcada linearmente para representar 100 pontos (n).
A escala H foi marcada de acordo com os logaritmos de (1 + i), com taxas de juros começando em 0 e indo até 10%. A escala I foi marcada de acordo com o logaritmo da quantidade resultante (A). Um cálculo feito para o valor de A que resultaria de 1 a 10% por 100 anos, e este valor foi usado como o valor máximo para A.
Aqui está um problema típico:
Quanto tempo levaria para aumentar seu dinheiro 5 vezes a uma taxa de juros de 6%, composta por semestre? Neste caso, o valor dos juros por período (semestre) é de 3%. Defina a escala H no potenciômetro Y a 3% de juros.
Defina a escala I no potenciômetro Z em 5,00 (cinco vezes seu 1,00). Gire o potenciômetro X e encontre a resposta para os períodos numéricos em cerca de 54. Isso representa 54 meios anos ou 27 anos completos. Assim seu dinheiro aumentaria 5 vezes em 27 anos com 6% de juros compostos semestralmente.
Alcance de um projeto
Agora um problema tradicional que está intimamente associada a história dos computadores analógicos. Trata-se do cálculo do alcance de um projétil disparado por um canhão ou outra arma, em função do seu ângulo de tiro, conforme mostra a figura 2.
Um conjunto extra de escala deve ser utilizado para estes cálculos. Este conjunto é mostrado na figura 3, sendo fornecido com o kit que tomamos como referência.
As escalas J, K e L fornecem cálculos para o alcance (R) de um projétil. A Fig. 1 mostra a trajetória de um projétil disparado de uma arma em A. A velocidade inicial do projétil é V. O ângulo em que a arma é apontada para cima a partir do base é θ (a letra grega “theta”). Estas duas quantidades determinam o alcance (distância horizontal percorrido pelo projétil no nível do solo).
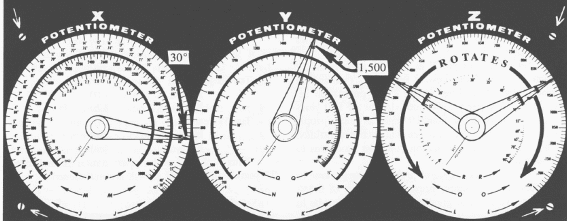
Tente este problema: uma arma está posicionada em um ângulo de 30° a partir do chão. Seu projétil tem velocidade de 1.500 (veja nota) pés por segundo. Quão longe ele irá viajar antes de bater no chão? Em outras palavras, qual é o seu alcance?
Defina o ângulo em 30° na escala J do potenciômetro X
Defina a velocidade de 1.500 pés por segundo na escala K do potenciômetro Y
Encontre a resposta da maneira usual na escala L do potenciômetro Z.
A resposta estará em 61.000 pés.
Tente este problema: O projétil de um canhão tem uma velocidade inicial de 1.800 pés por segundo. Em que ângulo a partir d chão deve ser inclinado apara acertar em um objeto 40.000 pés de distância?
Defina 40.000 na escala L do potenciômetro Z.
Defina 1.800 na escala K do potenciômetro Y.
Encontre a resposta da maneira usual na escala J do potenciômetro X.
A resposta é cerca de 23°. Observe que existe outro ponto de resposta possível, 67°. Isso significa que se o a arma fosse apontada para cima (67°), acertaria do mesmo modo como quando apontado para baixo (2 3 °). Observe que os dois ângulos para cada ponto na escala J sempre somam 90°. Os ângulos são complementares. Eles estão relacionados conforme mostrado na figura 4.
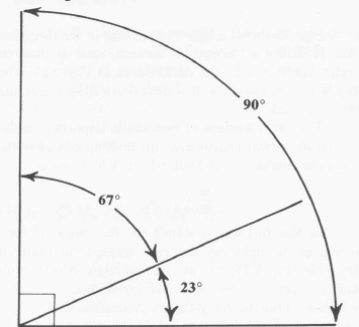
Por que esse conjunto de escalas fornece respostas corretas? (Algum conhecimento de trigonometria será necessário para entender as explicações para todos os funções do conjunto extra de escalas que você tem no computador. No entanto, deve ser possível para resolver os problemas com o computador até se as explicações não forem totalmente compreendidas.)
A fórmula para o alcance de um projétil é:
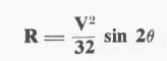
(Se você estiver interessado na derivação desta fórmula, você o encontrará em alguns livros didáticos de física da faculdade e mesmo do curso médio).
Podemos reescrever isto como:
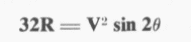
Considere V2 como uma quantidade variável e sen 2θ como outra. A expressão acima então se assemelha a forma X.Y = Z podendo, portanto, ser resolvida por seu computador, desde que as escalas sejam marcadas corretamente.
A posição horizontal de uma arma ocorre quando a arma está em um ângulo de 0 ° em relação ao solo. Verticalmente a arma posicionada está em um ângulo de 90 °. Os senos dos ângulos começam em um valor de 0 para 0° e vão até um valor de 1 para 90°.
No seu computador, os valores dos senos de todos os ângulos de 0° a 90° foram marcados fora do círculo na escala J. (veja nota no final do artigo)
Agora observe que a fórmula se refere a um ângulo de 2θ. Isso significa que quando a arma está inclinada para um ângulo (θ ) de 45°, o ângulo 2 θ será de 90°. Portanto, marcamos o ângulo máximo no final da escala 45°, não 90°. É neste ângulo que o alcance máximo é obtido.
Observe que a escala J não é linear (uniformemente espaçada), mas que os espaçamentos para os ângulos diminuem conforme você dê a volta em ângulos maiores de até 45°. Observe também que ao lado de cada ângulo está seu complemento. Isto ocorre porque se você dobrar um ângulo (2 θ) o valor de seu seno é o mesmo que dobra seu complemento.
Foi decidido definir o valor máximo do velocidade de 2.000 pés por segundo, como sendo razoável para velocidades do projétil. A escala era então marcada de acordo com V2, não V. Assim, a escala K do potenciômetro Y mostra espaçamentos que não são lineares, mas que aumentam rapidamente.
Quando os ponteiros para X e Y são definidos no maiores valores (extrema direita das escalas), devemos obter o maior valor para Z. O cálculo foi, portanto, feito do intervalo de θ = 45 ° (o máximo de um) e a velocidade máxima de 2.000 pés por segundo. Esse alcance chega a 125.000 pés (125 Mm)..
Este valor foi então definido na extremidade final do dial L do potenciômetro Z. Os números da escala L foram então subdivididos uniformemente (linearmente).