Este artigo aparece em outras versões neste site, inclusive em nosso livro Curso de Eletrônica – Telecomunicações 1. O artigo em sua versão original saiu num livro publicado em 1992, por isso não conta com algumas tecnologias mais modernas, mas é ainda importante para estudos, principalmente nos cursos de telecomunicações.
Para transmitir sinais de radio levando informações, como por exemplo som, imagem, etc. precisamos de equipamentos eletrônicos denominados transmissores.
Os transmissores produzem correntes de altas frequências que aplicadas a uma antena produzem no espaço perturbações denominadas ondas de rádio ou ondas eletromagnéticas. Estas ondas se propagam com a velocidade da luz (300 000 quilômetros por segundo) podendo ser captadas por equipamentos denominados receptores.
Para gerar as correntes de alta frequência, dependo do tipo de onda que desejamos irradiar (potência e frequência) precisamos de circuitos específicos.
A estrutura básica de um transmissor depende então de sai finalidade.
Damos a seguir a estrutura na forma de blocos de um transmissor típico, que servirá de base para o desenvolvimento deste livro. Transmissores com mais ou menos blocos podem ser encontrados dependendo da aplicação. A estrutura de um transmissor é então mostrada na figura 1.
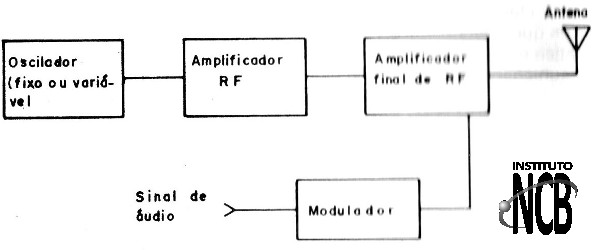
Um transmissor telegráfico pode tr apenas um ou dois blocos, sem a modulação já que os sinais são simplesmente a própria onda interrompida regularmente por uma manipuladora modulação, já que os sinais São simplesmente a própria onda interrompida regularmente por um manipulador
Um transmissor muito simples de AM ou FM pode ter um bloco oscilador apenas que já inclui o modulador e é ligado diretamente à antena.
Um transmissor de alta potência, por outro lado, pode ter muitos blocos amplificadores.
Finalmente, um transmissor de TV tem um modulador complicado que possui diversos circuitos de áudio e vídeo que devem ser combinados para serem transmitidos.
Analisemos cada bloco.
OS OSCILADORES
Para gerar os sinais nas frequências que devem ser transmitidas ou em frequências apropriadas (veremos que nem sempre o sinal gerado e o transmitido), usamos circuitos eletrônicos denominados osciladores.
Dependendo do componente usado (válvula, transistor comum ou transistor de efeito de campo) temos diversas disposições dos componentes de polarização e de acordo com estas disposições o circuito recebe seu nome.
Cada tipo de oscilador tem uma faixa de utilidade determinada que deve ser considerada num projeto.
Vamos examinar alguns osciladores.
a) Oscilador Hartley
Este tipo de oscilador é indicado para frequências que vão de alguns quilohertz e mesmo áudio, até aproximadamente 50 MHz. Na figura 2 temos o circuito básico usando um transistor.
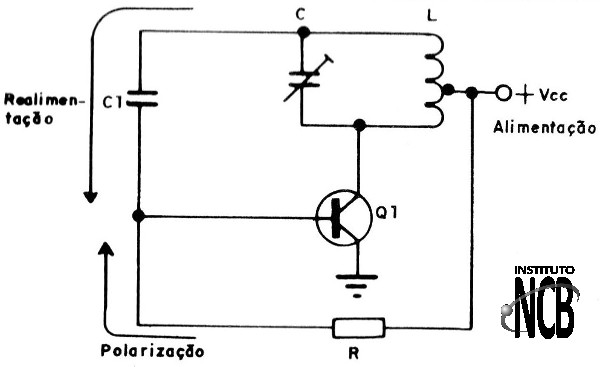
A bobina possui uma derivação por onde parte do sinal é levado à base do transistor, produzindo assim a realimentação que mantém o circuito em funcionamento.
Esta bobina e o capacitor em paralelo determinam a frequência de operação do circuito. Para mudar a frequência de operação temos duas possibilidades: usamos um núcleo ajustável de ferroxcube (PHILIPS COMPONENTS) para a bobina ou então usamos um capacitor variável ou trimmer em paralelo.
O transistor usado deve apresentar um bom ganho na frequência de oscilação para que o circuito possa entregar parte do sinal gerado aos elementos externos.
Na figura 3 temos um oscilador Hartley usando uma válvula.
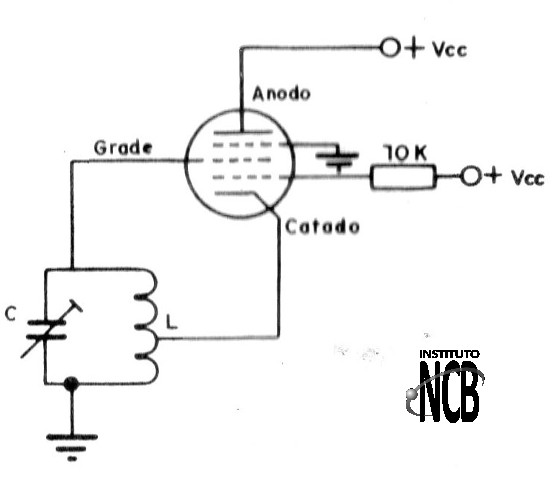
Com bons transistores de potência e válvulas pentodo, podemos obter deste circuito potências de ate algumas dezenas de watts, possibilitando assim a construção de transmissores muito simples com uma única etapa.
b) Oscilador Colpitts
Neste oscilador a derivação que permite a reaplicação do sinal à base do transistor (ou grade de uma válvula) para manter as oscilações, não é feita por uma derivação na bobina, mas sim por uma derivação por meio de capacitores, conforme mostra a figura 4.
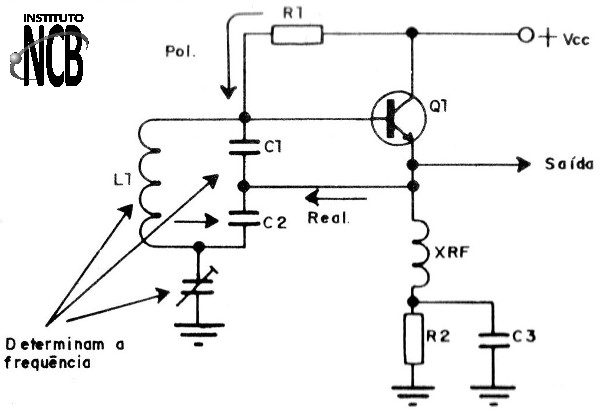
Aqui também a frequência é determinada pela bobina e pelos capacitores em paralelo, Estes componentes podem ser variáveis de modo a se ajustar a frequência do circuito.
Os osciladores Colpitts se prestam a operação numa faixa de frequência que vai de algumas dezenas de quilohertz até 50 ou 60 MHz.
No entanto, a potência que podemos obter e menor do que os osciladores Hartley.
Na figura 5 temos o oscilador em questão na versão com transistor de efeito de campo (FET).
c) Oscilador de Bloqueio
Neste oscilador a realimentação é feita por um segundo enrolamento na bobina de carga. A bobina de carga tem um capacitor em paralelo que determina a frequência de operação do circuito. Tanto a bobina como o capacitor podem ser variáveis para modificar a frequência de funcionamento do oscilador. Na figura 6 temos o diagrama de um oscilador deste tipo usando um transistor comum.
Este oscilador se presta a uma operação em frequências de até pouco mais de 20 MHz e sua potência não é muito grande.
A versão usando válvula é mostrada na figura 7.
d) Oscilador a cristal
Os cristais de quartzo são elementos que podem controlar a frequência de um oscilador com grande precisão. Estes cristais são usados em transmissores que operam numa única frequência que precisa ser mantida estável com grande precisão como, por exemplo, numa estação de rádio.
Diversas configurações podem ser feitas para se usar um cristal no controle de frequência, inclusive com os circuitos de osciladores já vistos.
Assim, podemos ter o Oscilador Pierce controlado a cristal que é mostrado na figura 8.
Neste circuito o funcionamento é idêntico ao oscilador Hartley convencional, com a diferença de que quem- determina a frequência é o cristal, e a bobina de carga com o capacitor em paralelo devem ser simplesmente ajustadas para a frequência do cristal, de modo a se obter o rendimento ideal do sistema.
Na figura 9 temos um oscilador Colpitts com cristal, em que o princípio também é o mesmo do original sem o cristal, com a diferença de que o cristal é que determina a frequência de operação.
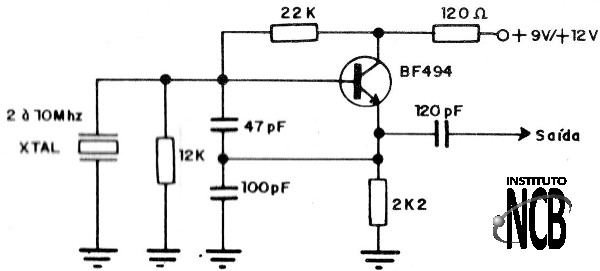
d) Oscilador de Base-comum
Ligado em base comum os efeitos da capacitância de um transistor diminuem e sua operação pode chegar a frequências muito altas. Este oscilador é pois usado em frequências acima do 20 MHz chegando a 300 ou 400 MHZ com facilidade.
Na figura 10 temos um circuito de um oscilador de base-comum com um transistor.
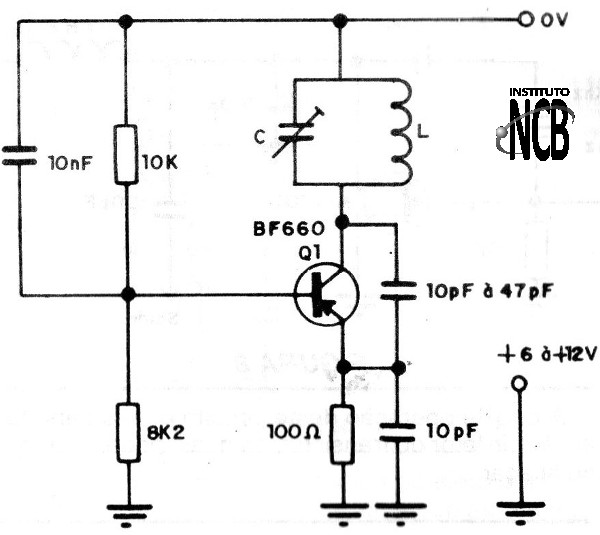
A realimentação que mantém a oscilação, vem através do capacitor entre coletor e emissor do transistor, que é um componente muito importante neste oscilador.
CALCULO DE FREQUENCIA
Conforme vimos, a frequência dos osciladores que não sejam controlados por cristal e determinada por um circuito ressonante LC, conforme mostra a figura 11.
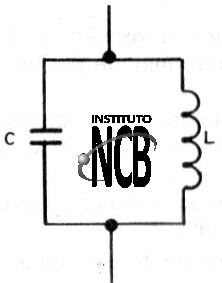
Um dos problemas que encontra o projetista de transmissores ou mesmo o montador que deseja fazer adaptações, e calcular L e C para a frequência desejada.
A seguir veremos como calcular estes componentes e alguns critérios que facilitam o projetista.
A fórmula que permite calcular a frequência e a (1)
f = 1 / ( 2π x LC )
Nesta fórmula, L é a indutância da bobina em henry (H) ,
C é a capacitância do capacitor em farads (F)
f é a frequência em hertz (Hz)
Pi é a constante universal que vale 3,14
Nos cálculos práticos e preciso tomar alguns cuidados, pois podemos escolher uma frequência e fixar a bobina para chegar a um capacitor cujo valor e impossível de obter. Por outro lado, se fixarmos de forma errada o capacitor para uma determinada frequência podemos chegar a uma bobina impossível de construir.
A experiência nos permite escolher certos valores de forma que as coisas fiquem mais fáceis.
Assim, uma vez escolhida a frequência, fixamos o valor do capacitor dentro de uma faixa conhecida, de modo que a bobina possa ter um valor fácil de se obter.
Urna tabela ajuda o leitor a fixar o capacitor, tomando como base os valores que são alcançados por trimmers e variáveis comerciais. Temos então a seguinte tabela:
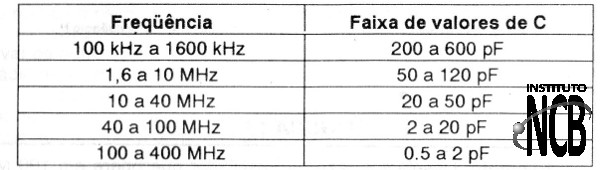
Com a fixação destes valores fica fácil chegar a bobinas facilmente enroláveis com fios comuns, fôrmas comuns e tamanhos não muito pequenos, nem muito grandes.
É importante que o leitor tenha em conta que usando um trimmer, por exemplo, de 2-20 pF isso significa que a frequência poderá variar entre dois valores quando este componente for ajustado.
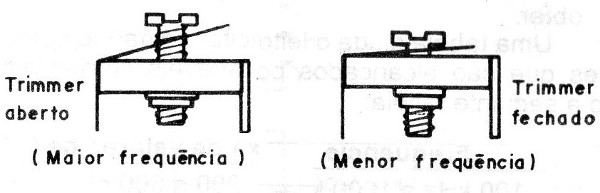
Assim, se fixarmos o valor da frequência desejada com o trimmer todo fechado, isso significa que a frequência aumentará até um valor limite conforme mostrado na figura 12.
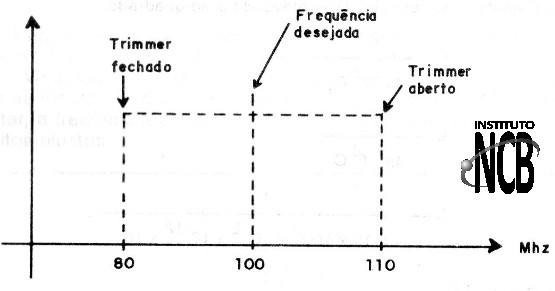
Assim, ao fazer o cálculo devemos tomar um valor máximo de um trimmer ou variável para uma frequência abaixo da que desejamos e depois verificar se, com o valor mínimo a frequência sobe para além do valor que desejamos, varrendo assim no ajuste uma boa faixa. Nesta faixa deve estar a frequência que precisamos, veja na figura 13.
Vamos dar um exemplo de cálculo a seguir:
Exemplo: Desejamos fazer um oscilador que opere em 100 MHz para um transmissor de FM usando um trimmer 2-20 pF. Qual deve ser o valor da bobina:
Devemos em primeiro lugar converter as unidades lembrando que picofarads equivalem a 10-12 Farads e que megahertz equivalem a milhões de Hertz ou 106 Hertz.
Assim, aplicando esses valores a fórmula conforme mostra o procedimento, temos o valor final da bobina:

Temos de usar uma bobina de 1/4 uH ou 0,25 uH.
Evidentemente, bobinas com valores como este não podem ser encontradas prontas no comércio, mas devem ser enroladas pelo montador.
Em muitos projetos encontramos já informações de quantas espiras de determinado fio devem ser enroladas e em que fôrmas para se obter a indutância desejada, mas se o leitor faz seu próprio projeto isso não ocorre.
Como calcular as dimensões de uma bobina a partir de sua indutância?
Também aqui é interessante termos certas regras práticas para não corremos o risco de encontrar dimensões ou número de voltas impossíveis.
Sabendo mais ou menos de que tamanho deve ficar a bobina e fácil levar os outros parâmetros a valores lógicos, de modo a termos uma bobina “fácil" de enrolar.
Também devemos levar em conta que elementos influem na indutância de uma bobina e isso será estudado a seguir antes de ensinarmos como fazer seu cálculo a partir da Fórmula 2.
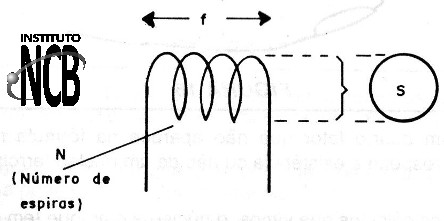
L = 1,257 x [ (n2 x S) / (108 x I) ]
Nesta fórmula:
L é o coeficiente de autoindução da bobina em Henry (H)
n é o número de espiras
S é a secção abrangida por uma espira em centímetros quadrados
I é o comprimento da bobina em centímetros.
Para estes cálculos estamos tomando como base uma bobina cilíndrica sem núcleo com formato igual ao mostrado na figura 14.
Vejamos como as diversas grandezas desta fórmula, se alteradas influem na indutância da bobina. Lembramos que se a indutância da bobina aumentar, a frequência do circuito diminui, o que deve ser levado em conta em muitos ajustes.
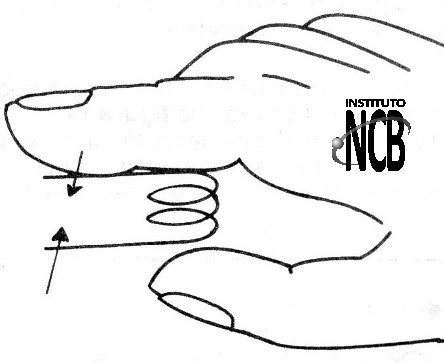
a) Número de espiras
A indutância da bobina depende diretamente do número de espiras, de modo que aumentando o número de espiras de uma bobina, sua indutância também aumenta e portanto a frequência do circuito diminui.
E comum nos processos de ajuste retirarmos algumas espiras de uma bobina para diminuirmos sua indutância e assim aumentar a frequência do circuito.
b) Área
A área de uma espira depende do diâmetro de bobina e influi de modo direto na sua indutância. Assim, aumentando o diâmetro de uma bobina, sua indutância aumenta e com isso a frequência do circuito em que ela se encontra diminui.
Se vamos enrolar uma bobina com um diâmetro menor para um circuito, devemos compensar isso com o aumento do número de espiras, ou de outra forma. Duas bobinas com o mesmo número de espiras e mesmo comprimento, oscila na frequência mais alta com o mesmo capacitor, a de menor diâmetro.
c) Comprimento
A indutância depende de maneira inversa desta grandeza, o que quer dizer que se apertarmos as espiras, de uma bobina, aumentamos sua indutância e com isso diminuímos a frequência do circuito oscilador em que ela se encontra.
Um procedimento comum no ajuste de transmissores é mostrado na figura 15 e consiste em apertarmos as espiras da bobina para diminuirmos a sua frequência.
d) Núcleo
Um quarto fator que não aparece na fórmula, mas é muito importante, diz respeito a existência ou não de um núcleo ferromagnético na bobina.
Para os cálculos que vimos, o núcleo é o ar, que tem uma "permeabilidade" igual a 1. No entanto, existem materiais que tem permeabilidade maior e que, portanto, se introduzidos no núcleo de uma bobina aumentam sua indutância.
Dentre estes materiais citamos os ferrites que permitem multiplicar a indutância de uma bobina se usados como núcleo, conforme mostra a figura 16.
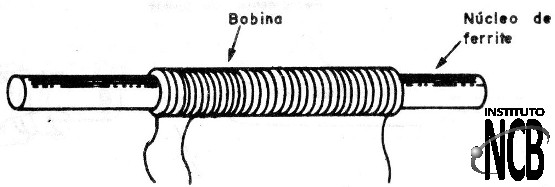
Em algumas bobinas este material pode movimentar-se no seu interior e quando faz isso, modifica a indutância alterando, pois a frequência do circuito oscilador.
Quando o núcleo penetra na bobina sua indutância aumenta e com isso a frequência de operação do circuito diminui.
Na figura 17 temos um exemplo de bobina ajustável usando um núcleo com rosca para poder penetrar na forma.
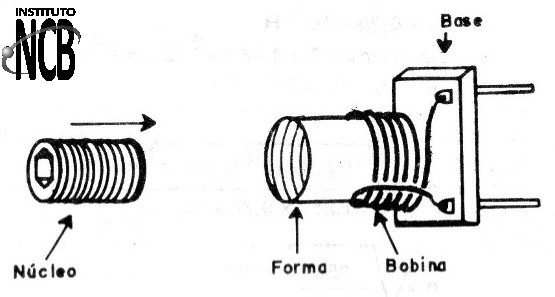
Usando uma bobina desta num oscilador, podemos ter um capacitor fixo em lugar do trimmer ou variável, já que o ajuste de frequência será feito no núcleo da bobina.
E interessante notar que qualquer objeto de metal que se aproxime de uma bobina pode influir na sua indutância.
Assim, uma chave defenda metálica ao se aproximar de uma bobina para um ajuste do núcleo, com sua presença aumenta a indutância e diminui a frequência. Feito o ajuste, quando a chave se afasta a indutância diminui e a frequência aumenta saindo do ponto de ajuste.
Por este motivo os ajustes dos núcleos das bobinas devem ser feitos com ferramentas próprias não metálicas, normalmente de madeira ou plástico, conforme mostra a figura 18.
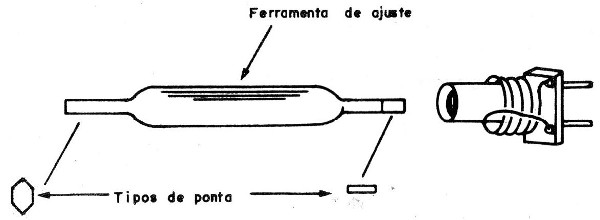
Damos a seguir o procedimento para o cálculo da bobina de 0,25 uH de nosso transmissor usando a fórmula indicada. Esta bobina terá um núcleo de ar e fixamos o seu diâmetro em 1 cm e seu comprimento também.

CIRCUITOS PRATICOS
A partir do que foi visto, podemos dar diversos circuitos práticos de osciladores que podem servir de base para transmissores, ou mesmo funcionar como pequenos transmissores de onda contínua ou modulados externamente, conforme mostraremos ainda neste livro.
1. Oscilador Hartley Prático
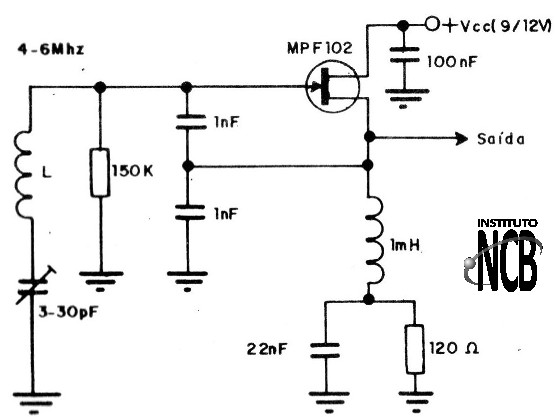
Este oscilador pode ser usado para produzir sinais na faixa de 100 kHz até aproximadamente 20 MHz com uma potência de algumas dezenas até centenas de miliwatts. Para frequências até 10 MHz podemos usar transistores de silício de uso geral como o BC547 ou BC548 e para frequências maiores devemos usar um BF495 ou equivalente. Para um pouco mais de potência alimentando o circuito com 12 Volts podemos usar um BD135 ou equivalente todos estes transistores são supridos no mercado nacional, portanto, fáceis de se achar.
Na figura 19 damos o oscilador Hartley prático.
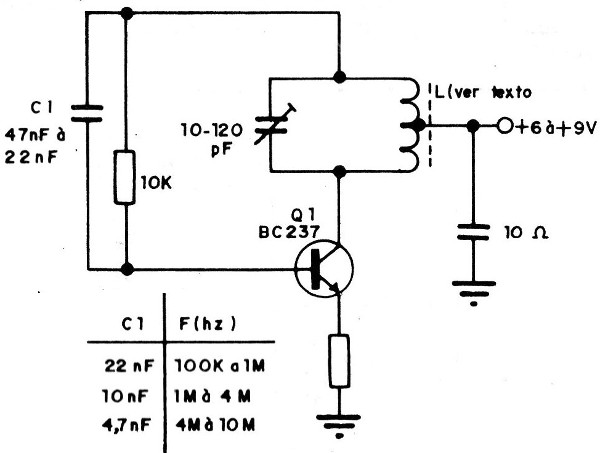
CV e L dependem da frequência. L será enrolada num bastão de ferrite de 1 cm de diâmetro e o número de voltas depende da frequência. Para todas as faixas o fio pode ser de 26 a 30. O comprimento do bastão de ferrite variará entre 10 e 20 cm, conforme precisemos enrolar mais ou menos espiras. O capacitor CV também depende da frequência. Damos na tabela abaixo os valores destes componentes:
100 kHz a 500 kHz: L = 250 espiras
CV = 200 a 500 pF (máxima capacitância)
500 a 2000 kHz : L = 100 espiras
CV : 200 a 500 pF (max)
2 MHz a 5 MHz : L = 40 espiras
CV = 120 a 300 pF
5 a 12 MHz: L = 20 espiras
CV = 50 a 120 pF
12 a 20 MHz : L = 15 espiras
CV : 20 a 100 pF
Evidentemente, em função do material usado e das tolerâncias dos componentes, pequenas diferenças podem ser encontradas na frequência geral que devem ser compensadas por alterações do número de espiras.
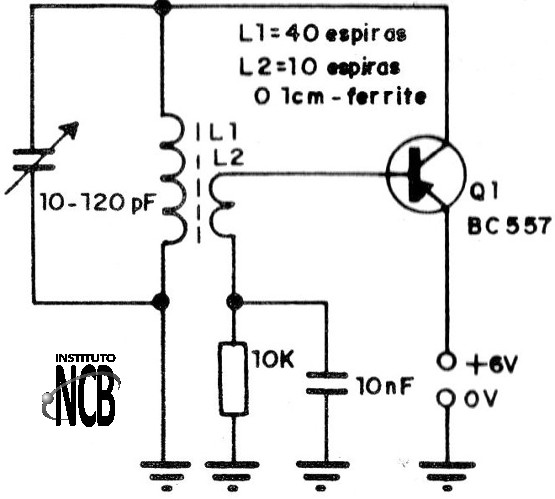
2. Oscilador de bloqueio
Este oscilador fornece uma potência de algumas dezenas de miliwatts em frequências de até 10 MHz aproximadamente. Com transistores de maior potência e alimentação de 12V ou mesmo mais, podemos aumentar a intensidade do sinal gerado. O circuito do oscilador de bloqueio é mostrado na figura 20.
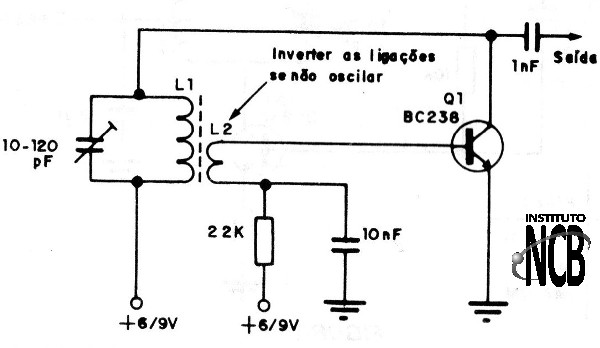
A bobina é enrolada num bastão de ferrite de 10 a 20 cm de comprimento e o fio usado pode ser de 26 ao 30. O número de espiras, assim como o valor de CV depende da faixa de frequências gerada.
Podemos indicar os seguintes valores aproximados:
100 kHz a 500 kHz :
L1 = 250 espiras
L2 = 40 espiras
CV = 200 a 500 pF
500 a 2000 kHz :
L1 = 100 espiras
L2 = 25 espiras
CV = 150 a 400 pF
2 MHz a 5 MHz :
L1 = 50 espiras
L2 = 10 espiras
CV = 50 a 200 pF
5 MHz a 10 MHz :
L1 = 30 espiras
L2=: 8 espiras
CV = 20 a 150 pF
Também neste caso devemos considerar as tolerâncias dos componentes usados.
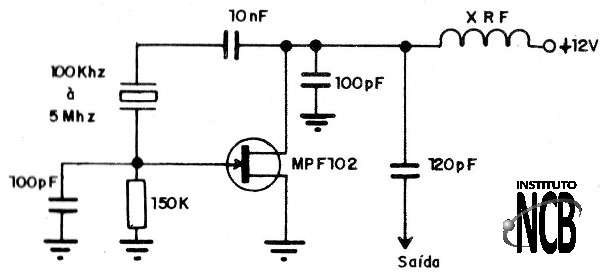
3. Oscilador Base-Comum
Este oscilador, melhor que os anteriores se presta a produção de sinais de frequências mais altas. Podemos usá-lo de 20 MHz até 200 MHz desde que escolhamos transistores apropriados. Os capacitores devem ser todos cerâmicos. A bobina deve ter núcleo de ar e o fio usado será de 22 a 26. O diâmetro da bobina é de aproximadamente 1 cm.
Na figura 21 temos o circuito do oscilador que fornece uma potência de algumas dezenas de miliwatts, mas que pode ser aumentada com o uso de um transistor como o 2N2222A ou BD135 dependendo da faixa gerada.
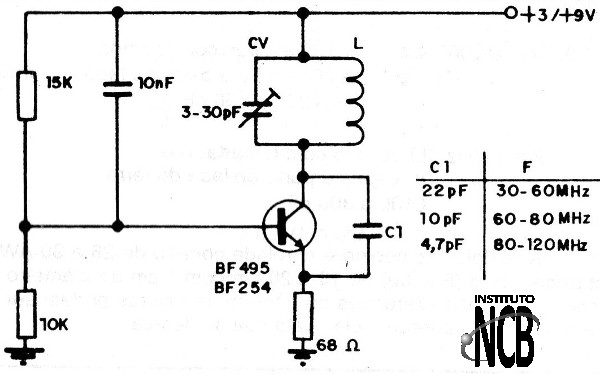
Os capacitores devem ser todos cerâmicos. No circuito sugerido o transistor pode ser o BF495 ou qualquer equivalente de pequena potência de RF de acordo com a frequência a ser produzida.
Para as frequências geradas damos os valores dos componentes:
20 a 50 MHz:
L = 9 espiras
CV = 3 a 30 pF
C = 47 pF
50 a 100 MHz :
L= 5 espiras
CV = 3 a 30 pF
C = 12 pF
100 a 150 MHz
L= 3 espiras
CV = 3-30 pF
C = 4,7 pF
150 a 200 MHz : L = 2 espiras
CV : 3 - 30 pF
C = 1 pF
Alterações nos valores podem ser necessárias de acordo com os componentes. Por exemplo, um valor maior de C pode exigir a diminuição de espiras para se chegar a frequência desejada. Alterações de espiras para mais ou para menos podem ocorrer em alguns casos para se chegar a frequência desejada.
4. Oscilador com FET
O oscilador Hartley com FET da figura 22 é bom para frequências até aproximadamente 5 MHz.
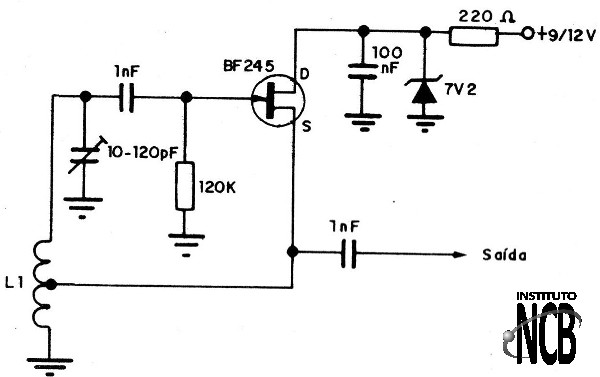
O FET é comum de junção BF245 e a alimentação pode ficar entre 6 e 12 Volts.
A bobina e CV dependem da frequência gerada conforme informamos a seguir:
500 kHz a 2000 kHz :
L = 100 espiras com tomada na 20ª espira a partir do lado do terra.
CV : 200 a 500 pF
2 a 5 MHz :
L = 50 espiras com tomada na 20ª espira a partir do lado do terra.
CV : 100 a 300 pF
Nos dois casos a bobina e enrolada com fio de 26 a 30 AWG num bastão de ferrite de 10 a 20 cm com 1 cm de diâmetro aproximadamente. Pequenas alterações no número de espiras podem ser necessárias para se chegar a frequência exata que se deseja.
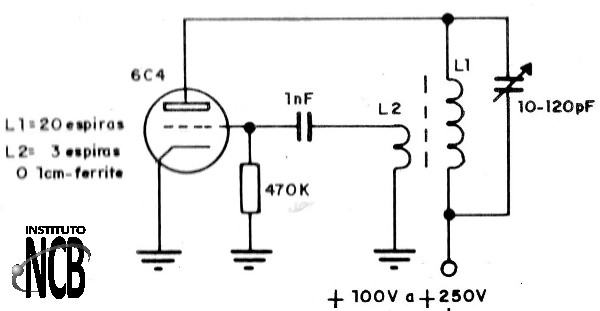
5. Oscilador com Válvula Pentodo
Válvulas pentodo podem funcionar com osciladores de potências na faixa de 2 a 20 watts, como o que usa a 6L6 mostrada na figura 23 e que alcança os 20 MHz com facilidade.
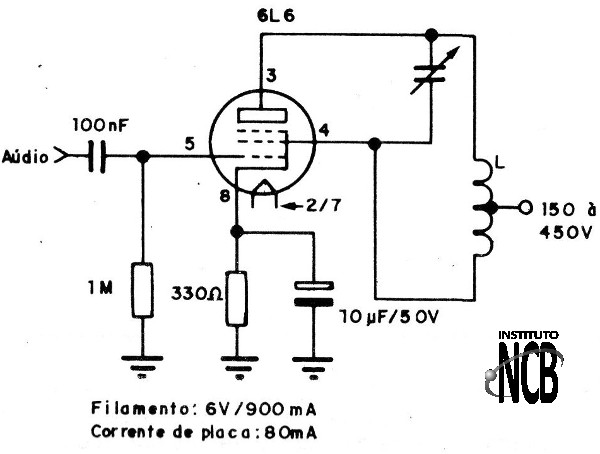
A alimentação de placa deve ser feita com tensões de 100 a 250 volts e corrente de 50 a 200 mA. O filamento exige 1 ampère com tensão de 6 Volts.
A fonte para este circuito oscilador pode ser a mostrada na figura 24 que usa um transformador de dois enrolamentos secundários.
Ligado a uma antena este oscilador pode ser usado como potente transmissor de CW na faixa de ondas curtas (160, 80, 40 ou mesmo 20 metros).
A bobina terá as seguintes características assim como CV:
500 a 2000 kHz :
L = 100 espiras de fio 26 em fôrma sem núcleo com 2,5 cm de diâmetro e tomada central.
CV = 200 a 400 pF
2 a 7 MHz :
L = 40 espiras de fio 28 em fôrma de 2,5 cm de diâmetro sem núcleo e tomada central.
CV = 200 a 400 pF
7 a 15 MHz :
L = 25 espiras de fio 28 em fôrma de 2,5 cm de diâmetro sem núcleo com tomada central.
CV = 50 a 200 F
Também neste circuito variações podem ser necessárias em função da tolerância dos componentes usados. A fonte deve ser montada em chassi blindado juntamente com este oscilador para que não ocorram roncos.

















